




Министерство образования Республики Беларусь
Белорусский Национальный Технический Университет
Кафедра“Гидропневмоавтоматика и гидропневмопривод”
Группа 101714
Расчетная работа №4
по дисциплине “Теория автоматического управления”
Выполнил:
Руководитель:
Минск 2007
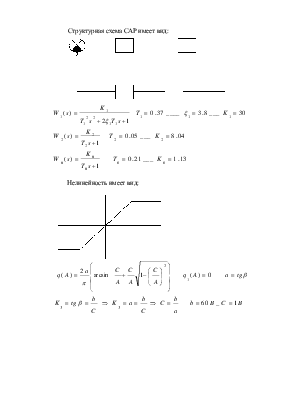
Структурная схема САР имеет вид:
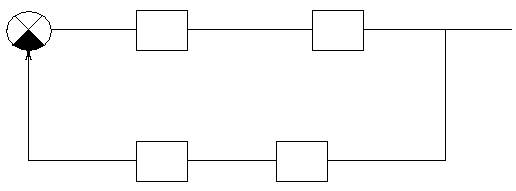
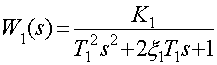
![]()
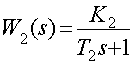
![]()
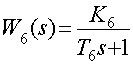
![]()
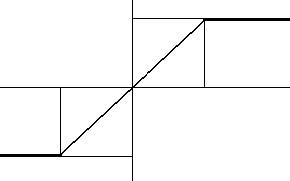
Нелинейность имеет вид:
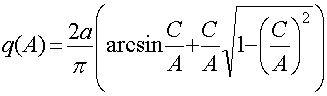
![]()
![]()
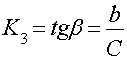
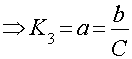
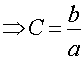
![]()
· Запишем уравнение движения гармонически линеаризованной нелинейной части.
По структурной схеме САР получаем уравнение движения линейной части
![]()
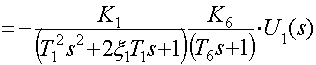
![]()
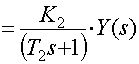
Решим данные уравнения совместно и получим
![]()
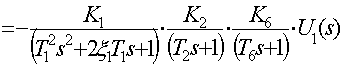
![]()
Полученное уравнение является уравнением движения линейной части.
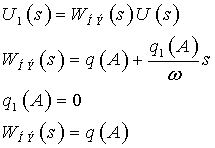
Данная нелинейность является однозначной.
![]() - уравнение
движения гармонически линеаризованного нелинейного элемента.
- уравнение
движения гармонически линеаризованного нелинейного элемента.
Для задания нелинейности, коэффициент гармонической нелинейности записывается в виде
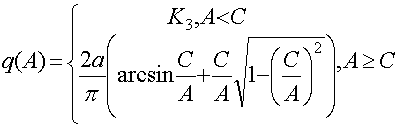
Запишем совместно уравнения движения линейной и нелинейной частей САР и получим
![]()
И полученное уравнение является уравнением движения гармонически линеаризованной системы.
· Уравнение полученное выше соответствует характеристическому уравнению
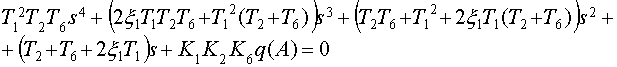
![]()
Для того чтобы найти условие существования в линеаризованном
уравнении движения, введем замену ![]()
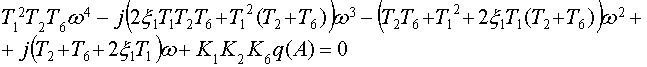 Выделим
вещественную и мнимую части, которые приравниваются к нулю, т.е. получается
система уравнений
Выделим
вещественную и мнимую части, которые приравниваются к нулю, т.е. получается
система уравнений
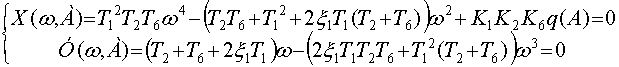
Из второго уравнения данной системы находим частоту периодического решения
![]()
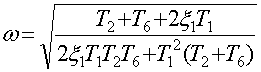
 После подстановки в первое уравнение системы
всех значений, получим связь амплитуды и периода решения с параметром системы
После подстановки в первое уравнение системы
всех значений, получим связь амплитуды и периода решения с параметром системы
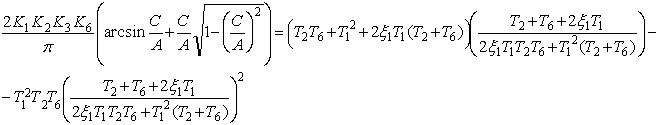
· Для исследования устойчивости периодического решения воспользуемся алгебраическим критерием
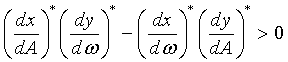
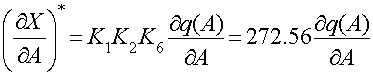
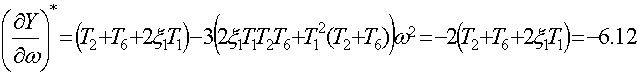
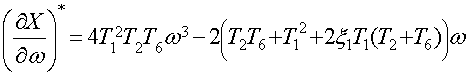
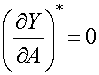
Тогда получим
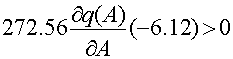
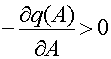
При ![]()
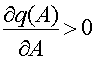 следовательно
автоколебания отсутствуют, т.к. при этом нелинейная САР превращается в линейную
следовательно
автоколебания отсутствуют, т.к. при этом нелинейная САР превращается в линейную
![]()
При ![]()
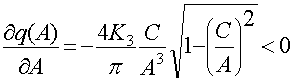
Теперь определим амплитуду автоколебаний нелинейной системы.
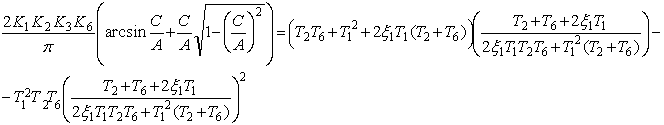
Данное уравнение, связывающее амплитуду автоколебаний с параметром системы, является трансцендентным.
Воспользуемся графо-аналитическим методом. Для этого решим
уравнение относительно коэффициента передачи ![]()
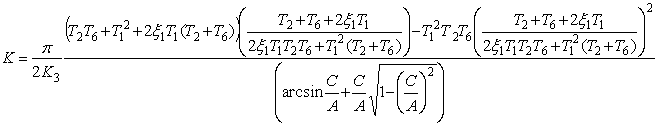
По данному выражению строим график зависимости ![]() .
.
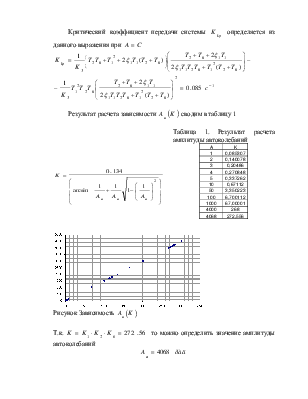
Критический коэффициент передачи системы ![]() определяется из
данного выражения при
определяется из
данного выражения при ![]()
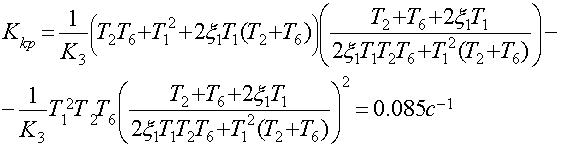
Результат расчета зависимости ![]() сводим в таблицу 1
сводим в таблицу 1
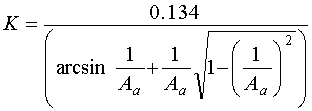
Таблица 1. Результат расчета амплитуды автоколебаний
|
A |
K |
|
1 |
0,085307 |
|
2 |
0,140078 |
|
3 |
0,20486 |
|
4 |
0,270848 |
|
5 |
0,337262 |
|
10 |
0,67112 |
|
50 |
3,350223 |
|
100 |
6,700112 |
|
1000 |
67,00001 |
|
4000 |
268 |
|
4068 |
272,556 |
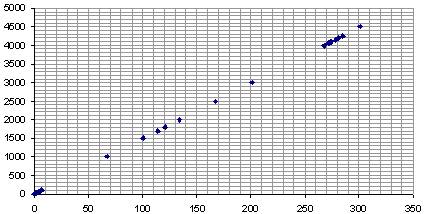
Рисунок Зависимость ![]()
Т.к. ![]() то можно
определить значение амплитуды автоколебаний
то можно
определить значение амплитуды автоколебаний
![]()
·
Частота автоколебаний
остается неизменной для любой переменной системы и согласно значению 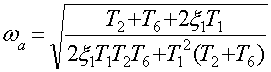 не зависит от коэффициента усиления системы и
не зависит от коэффициента усиления системы и
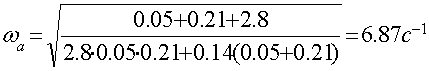
Значение амплитуды выходного сигнала ![]() можно определить
можно определить
![]()
![]()
![]()
Тогда получаем 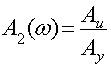
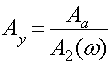
Подставим исходные значения, получим
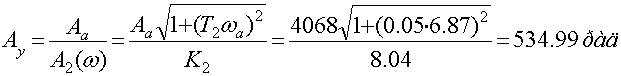
Найдем и построим область устойчивых состояний равновесия и автоколебаний в нелинейной САР от параметров 2-го звена.
Расчет проведем по формулам:
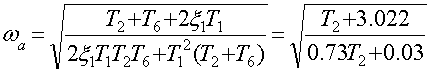
Т.к. ![]() не зависит от
не зависит от ![]() то график
зависимости
то график
зависимости ![]() будет выглядеть виде прямой параллельной оси
абсцисс.
будет выглядеть виде прямой параллельной оси
абсцисс.
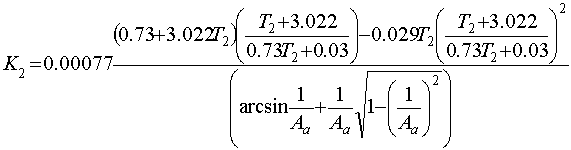
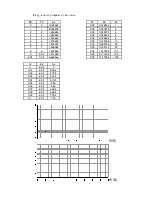
Результаты снесем в таблицы:
|
К2 |
T2 |
wa |
|
0 |
0 |
10,25264 |
|
1 |
1 |
2,306278 |
|
2 |
2 |
1,839846 |
|
3 |
3 |
1,650346 |
|
4 |
4 |
1,545869 |
|
5 |
5 |
1,479292 |
|
6 |
6 |
1,433037 |
|
7 |
7 |
1,398985 |
|
8 |
8 |
1,372848 |
|
9 |
8,04 |
1,371928 |
|
8,04 |
0,05 |
6,868366 |
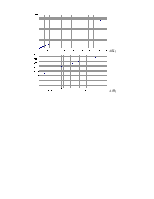
|
t2 |
K2 |
Aa |
|
0 |
8,04 |
0 |
|
0,01 |
8,04 |
348,6 |
|
0,02 |
8,04 |
407,5 |
|
0,03 |
8,04 |
461,5 |
|
0,04 |
8,04 |
510,5 |
|
0,05 |
8,04 |
555 |
|
0,06 |
8,04 |
596 |
|
0,07 |
8,04 |
633,5 |
|
0,08 |
8,04 |
668,5 |
|
0,09 |
8,04 |
700,5 |
|
0,1 |
8,04 |
730 |
|
T2 |
K2 |
Aa |
|
0,05 |
0,018436 |
1 |
|
0,05 |
0,030272 |
2 |
|
0,05 |
0,044272 |
3 |
|
0,05 |
0,058533 |
4 |
|
0,05 |
0,072885 |
5 |
|
0,05 |
0,145035 |
10 |
|
0,05 |
0,289706 |
20 |
|
0,05 |
0,724012 |
50 |
|
0,05 |
1,447952 |
100 |
|
0,05 |
2,171908 |
150 |
|
0,05 |
14,47928 |
1000 |
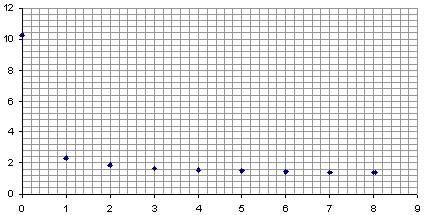 W(T)
W(T)
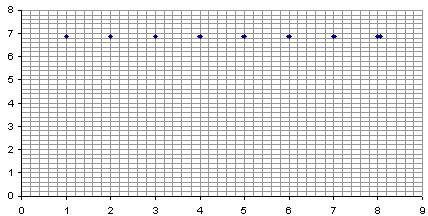 W(K)
W(K)
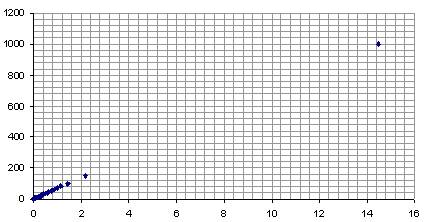 A(K)
A(K)
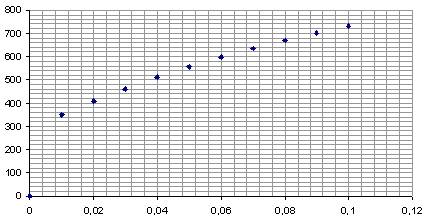 A(T)
A(T)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.