



 |
Все матрицы линейных цепей взаимосвязаны. Определение одной из них даёт возможность вычислить значения других. Кроме перечисленных выше на практике, при определённых условиях, используют гибридные Н-матрицы, обыкновенные А-или волновые Т-матрицы передачи.
Ниже рассматриваются результаты исследований Y и S-матриц с точки зрения идентификации параметров многополюсников. измерительные задачи решены на основе математического аппарата S-матриц, как наиболее простого и понятного решения подобных задач [1,2].
Измерения информации достаточной для определения S-матриц многополюсника производится относительно просто и может быть сведён к измерению модулей и разностей фаз комплексных напряжений на полюсных зажимах измерительной схемы. Применение современной измерительной аппаратуры при внедрении способов и устройств приведённых в работах [3,4], практически исключает из процесса измерения какие либо подстроечные операции .
Применение сложных алгоритмов расчёта не осложняют процесс измерения, так как современные ПК позволяют выполнять необходимые расчёты на фоне измерительных операций.
Физической основой S-параметров являются энергетические отношения между многополюсником и устройствами подключёнными к его входам полюсам. S- параметры многополюсника позволяют определить характер обмена энергии между многополюсником, источниками энергии и его нагрузками, подключёнными к его входам. Аналитическое описание процессов производится по значениям векторов падающих a волн, направленных к многополюснику, и отражённых b волн направленных от него (рис.1). Волны а и b нормированы таким образом, чтобысохранился принцип инвариантности мощности. По этому размерность каждой из составляющих векторов а и b в виде должна быть равна (Вт)0.5 [1, 2].
Связь между векторами а и b определяется матрицей рассеяния S. Матричное уравнение имеет вид
b=S*a. (1)
Для линейных, активных и пассивных многополюсников существует однозначная аналитическая связь между S- матрицами и матрицами проводимости Y, сопротивления Z. Элементы матриц Y и Z, рассчитанные через S- матрицу должны быть при этом нормированы. В важном для практики случае нормирования Y - матрица связывает вектор токов IH с вектором нормированных напряжений UH.
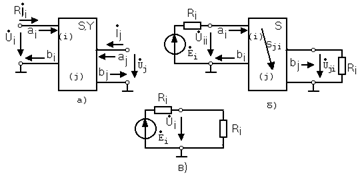 |
Рис. 1. Эквивалентный многополюсник: а-эквивалентная схема; б-нагруженный режим; в-режим калибровки.
В общем случае выбор значения активного нормирующего сопротивления произволен. На практике значения нормирующего активного сопротивления Ri для i-го полюса выбирают так, чтобы осуществлялся режим передачи наибольшей мощности от источников энергии к многополюснику и от многополюсника к нагрузкам (режим согласования). Чтобы осуществлялся принцип инвариантности мощности, нормированные токи и напряжения на входах полюсах многополюсника должны вычисляться по правилам
ÍiH=Íi(Ri) 0.5 ; ÚiH=Úi/(Ri) 0.5 (2)
где ÍiH, ÚiH- нормированные значения токов и напряжений для i-го полюса;
Íi, Úi- их ненормированные значения;
Ri- значения нормирующее сопротивление.
Чтобы адекватно установить связь между нормированными S- и У- матрицами, необходимо выполнить условия.
ÚiH=ai+ bi, ÍiH= ai- bi. (3)
Тогда из уравнения (3) следует, что
ai=(Úi/(Ri) 0.5 +Íi(Ri)) 0.5/2;
bi=(Úi/(Ri) 0.5 -Íi(Ri)) 0.5/2. (4)
Уравнения (4,3) имеют важное значение, так как они позволяют, по результатам измерения абсолютных значений комплексных токов и напряжений Íi и Úi вычислить необходимые для определения коэффициентов S- матрицы значения нормированных волн ai и bi[3].
Матричное уравнение связи векторов I и U имеет вид
I=YU, (5)
где Y- матрица многополюсника.
Решения уравнения (5) для нормировочных векторов IH и UH относительно векторов a и b с учётом уравнений (1) и (3) получаем матричное уравнение определяющие связь между нормированной матрицей проводимости YН и матрицей рассеяния S,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.