Алгоритмические методы измерения Y-параметров многополюсных радиокомпонентов, страница 2

Y^Н=(1-S)(1+S)^-1,                        (6)

где 1- единичная матица.

С другой стороны связь между S и Y^Н матрицами определяет формула.

S=(1-Y^Н)(1+Y^Н)^-1.                        (7)

Основное преимущество идентификации матрицы Y^Н по известной матрице S, по формуле заключается в том, что измерение информации, необходимой для определения коэффициентов S-матрицы может быть проведено при подключении к выходам многополюсника конечных активных или комплексных нагрузок  [3,4], тогда как способы экспериментального определения коэффициентов матрицы Y, связанны с реализацией опытов короткого замыкания, которые например при измерении активных многополюсников, выполнить сложно или вообще невозможно.

Методика измерений S-матриц [1,2] предусматривает следующие действия Многополюсник включают в согласованный СВЧ тракт, в котором отсутствуют (что практически неосуществимо) отражение волн от согласованных нагрузок и источников сигналов. Разделение волн на падающие и отражённые с целью определения их значений производится с помощью устройств типа направленных ответвителей.

Эквивалентная схема измерительной цепи без указания устройств разделения падающих и отражённых волн может быть сведена к виду, показанному на рис.1,б. Сущность метода измерения коэффициентов S- матрицы вытекает из анализа развёрнутой формы матричного уравнения относительно входов исследуемого многополюсника i и j

b_i=S_i1a₁+…+S_iia_i+…+S_ija_j+…+S_ina_n;

b_j=S_j1a₁+…+S_jia_i+…+S_jja_j+…+S_jna_n;           (8)

 

где  i=1,n; j=1,n;   n число входов-полюсов.

Для согласования режима (рис.1.б ) все падающие a_j волны при j<>i равны нулю, так как все волны b_j (j<>i) поглощаются нагрузочными резисторами. Тогда из уравнения (7) находим выражения для определения S_ii  диагональных и S_ji недиагональных коэффициентов S- матрицы

S_ii=b_i/a_i; S_ji=b_j/a_i.(9)

Для согласованного режима падающих a_j (j<>i) волны пассивных полюсов равны нулю, благодаря тому, что все волны b_j поглощаются резисторами. Таким образом напряжения Ú_ji будут пропорциональны волнам b_j. Падающие U_i волны, для активного полюса, к которому подключён источник сигнала, будут пропорциональны напряжению Ú_i которое вырабатывается на выходе генератора É_i, включённого по схеме рис.1.в. Так как напряжения Ú_ii (рис.1.б) равно сумме падающей a_i и отражённой b_i волн, то отражённая волна b_i будет пропорциональна разности напряжений Ú_ii и Ú_i. Таким образом, определение матрицы полюсных напряжений. U по схеме рис.1,б и вектора опорных напряжений по схеме рис.1.в служит предпосылкой для вычисления S- матрицы.

Введём нормированную матрицу передачи К^Н, коэффициенты которой определим через отношение полюсных Ú_ji и опорных Ú_iнапряжений по формуле

K_ji^H=(Ú_ji /Ú_ii )(R_i/R_j)^0.5                     (10)

Тогда при учёте выражений (1)-(8) в полном соответствии с положениями работы [3] получаем  матричное уравнение для расчёта матрицы рассеяния

S=K^H-1,                                (11) где 1-единичная матрица.

Подставим  (10) в (6) находим матричное выражение

У^H =2(K^H)^-1-1,                          (12)

Денормирование элементов матрицы У^H  производится по формуле

Y_ji= Y_ji^H /(R_iR_j)^0.5.                        (13)

Изложенный способ отвечает условиям измерениям в согласованных волноводных трактах при использовании активных полюсных нагрузках. В первом случае оптимальное условие измерения ограничивают волновые сопротивления трактов, 50 Ом или 75 Ом. Во втором случае оптимальное условие измерения нарушается с ростом частоты, так как обычные резисторы, кроме активной составляющей сопротивления имеют паразитные индуктивность и ёмкость. Измерительные цепи также имеют более или менее значимые паразитные индуктивности и ёмкости, которые приводят к искажению информации при расширении частотного диапазона.

В этой связи при организации измерений в широком диапазоне частот, возникает задача учёта реальных условий измерения, а именно, корректировка влияния паразитных параметров нагрузочных резисторов и элементов измерительных цепей.

Пусть реальное измерительное устройство отвечает схеме рис.2

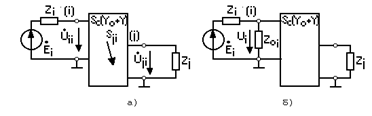Рис. 2. Реальная измерительная цепь: а- принципиальная схема; б- её формальное изображение