ГЛАВА 2. АЛГОРИТМИЧЕСКИЕ МЕТОДЫ ИЗМЕРЕНИЯ
ДИНАМИЧЕСКИХ ПАРАМЕТРОВ МАКРОМОДЕЛЕЙ МНОГОПОЛЮСНЫХ РАДИОКОМПОНЕНТОВ
2.1. Общие положения
В теории электрических цепей исключительное значение имеют матрицы Y - проводимости, Z - сопротивления, S - рассеяния, с помощью которых устанавливается связь между входными и выходными токами и напряжениями многополюсного электронного устройства. Особое значение при этом имеет волновая матрица рассеяния (S - матрица), свойства которой позволяют идентифицировать линейные параметры МП при режимах работы близких к реальным.
Перечисленные выше матрицы позволяют производить альтернативные определения состояний электрических цепей. Они применяются разработчиками электронных схем в зависимости от конкретных задач. Так Z -матрицы удобны для анализа электрических цепей методом контурных токов, Y - матрицы - методом узловых потенциалов, a S - матрицы для идентификации параметров многополюсников.
Все матрицы линейных параметров многополюсников взаимосвязаны. Определение одной из них даёт возможность вычислить значения остальных. Кроме перечисленных выше на практике при определённых условиях используют также гибридные матрицы, например обыкновенные А - или волновые Т - матрицы передачи.
Ниже рассматриваются результаты исследования Y - и S - матриц с точки зрения идентификации параметров многополюсника. Измерительные задачи решены на основе математического аппарата S - матриц, как наиболее простого и понятного [29, 53].
Измерения информации, достаточной для определения S - матриц многополюсника производится элементарно и может быть сведён, по существу, к измерению модулей и разностей фаз комплексных напряжений в рефлексных плоскостях (точках) измерительных цепей. Применение современной измерительной аппаратуры при внедрении способов и устройств, приведённых в работах [22-52] практически исключает при измерении какие-либо подстроечные операции, а также упрощает согласование измерительных цепей.
При этом необходимые сложные алгоритмы расчёта не осложняют процесс измерения при использовании современных персональных компьютеров в качестве ядра измерительной системы. Такие методы отвечают определению алгоритмических методов измерения.
Современным методам расчёта электронных схем наиболее отвечают Y -матрицы [1].
2.2.Матричное представление динамических параметров многополюсника.
2.2.1. Определение Yи Z матриц
Линейные динамические параметры многополюсника выражают связь токов и напряжений, которые вырабатываются на его входах-полюсах при подключении их к внешним электрическим цепям. Рассмотрим многополюсник рис.2.1 с числом полюсов n, в котором определены токи Íiи напряжение Úi для каждого i-ro входа. Напряжения Úi приложены между зажимами i-ro входа, один из которых представляет общую для входов-полюсов шину. Все токи Íi направлены к многополюснику, а напряжения Úi - от активного зажима к общей (нулевой) шине.
Пусть совокупность полюсных токов представляет вектор столбец I полюсных токов
I=[ Í1,…, Íi,…, Ín]T, (2.1)
а совокупность полюсных напряжений - вектор столбец U полюсных напряжений
U=[Úb...,Úi,...Ún]T. (2.2)
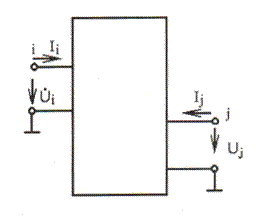 |
Рис. 2.1.- Формальная модель многополюсника
Если считать Uiзначения элементов вектора U заданными, значения Íi элементов вектора Iискомыми, то Ii можно рассматривать как линейную комбинацию, Ú1,Ú2,…, Ún т.е.
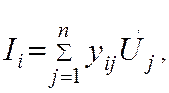 (2.3)
(2.3)
где уij - взаимная проводимость при i≠j или входная проводимость при i= j. В матричной форме уравнения (2.4) запишутся в виде:
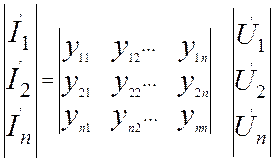 |
(2.4)
или
I=YU(2.5)
где Y - матрица проводимостей.
Если теперь считать Íi заданными величинами, aÚi искомыми, то по тем же соображениям U1 значение вектора U можно рассматривать как линейную комбинацию Í1, Í2 ,…, Ín т.е.
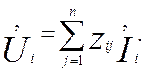
(2.6)
Из уравнения (2.6) после несложных рассуждений приходим к матричному уравнению, связывающему компоненты векторов U и I в виде
U=ZI (2.7)
где Z - матрица сопротивлений по структуре аналогичная матрице Y.
В САПР электронных схем (ЭС) матрицы Y радиокомпонентов или отдельных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.