Разработка универсального автоматизированного тестера радиоэлементов

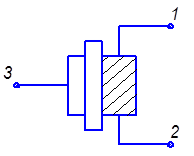
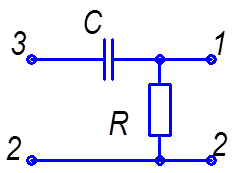
первых, указанным способом можно аттестовать компоненты производные от указанных на рисунок 2.12. Например, RC – структуру путём соответствующего включения в электрическую схему можно применять как форсирующую цепочку рисунок 2.15а, как интегрирующую структуру рисунок 2.15б или как дифференцирующую цепочку  рисунок 2.15в.

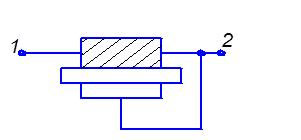
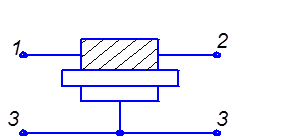
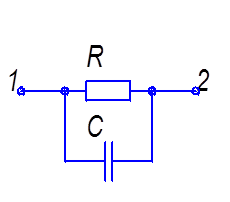
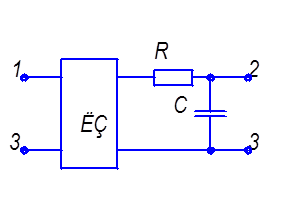
а)                                                                   б)                                          

в)

а) Форсирующая цепочка;

б) Интегрирующая цепочка; в) Дифференцирующая цепочка,

ЛЗ – линия задержки.

Рисунок 2.15- Способы использования RC – структуры

С другой стороны, модели РК, приведённые на рисунке 2.11 органически распространяются на большой класс акустоэлектронных устройств, для которых такие эквивалентные схемы рисунок 2.11, по-существу, служат схемами-прототипами этих устройств.

Формирование макромоделей пассивных РК на основе Y – параметров, экспериментальных данных, способов и устройств, признанных изобретениями не связано с трудоёмкостями принципиального характера.

Внедрение в практику измерений методов планирования эксперимента [15,17] позволяет при ограниченном объёме измерительных операций получить аналитические выражения для частотных характеристик коэффициентов Y – матрицы, которую будем рассматривать в виде Y(w). В зависимости от условий моделирования, которые определяют рабочий частотный диапазон, по матрице Y(w) можно формировать спектр дискретных по частоте Y – матрицы макромоделей с числом частных точек достатычных для получения достоверных результатов.

2.6 Встроенные макромодели транзисторов

К ним относятся модели для случая "большого" сигнала: биполярные транзисторы (БТ), арсенид – галиевые и МОП – транзисторы. Модели сепарабельные, то есть малосигнальная макромодель формируемая на основе модели для большого сигнала.

К достоинствам встроенных моделей можно отнести:

Возможность аттестации их параметров по справочным данным.

Сепарабельность.

Возможность построения ряда моделей для одного транзистора, отличающихся друг от друга уровнем сложности.

В основу модели БТ положены идеи выдвинутые Эберсом и Моллом и развитые для случая передаточной модели Логаном [8,9] или зарядовая модель Гуммеля – Пуна [13]. Полная встроенная модель представляется в виде адаптированной модели Гуммеля – Пуна, которая по сравнению с исходной моделью позволяет учесть эффекты возникающие при больших смещениях на переходах. Эта модель автоматически упрощается до более простой модели Эберса – Молла в версии Логана, если опустить некоторые параметры. Эквивалентная схема модели транзистора согласно [10] приведена на рисунке 2.16.

Всего аттестуется 55 параметров из них для описания модели Эберса – Мола достаточно использовать 49 параметров, задав 10 параметров, необходимых для описания модели Гуммеля – Пуна по умолчанию.

Всего по умолчанию могут быть заданы 54 параметра, что представляет пользователю широкий манёвр при формировании рабочих моделей.

Модель позволяет производить учёт температурных зависимостей параметров, путём аттестации 10 температурных коэффициентов и задания их области определения (четыре значения температуры и отношений температур). В числе аттестуемых параметров 10 температурных коэффициентов, однако, в доступных пользователю моделях используется только один из них [10].

Рассмотрим модель по Эберсу – Моллу, эквивалентная схема которой представлена на рисунке 2.17. В этом случае в качестве основных токов используются токи, собираемые p-n переходами и моделируемые генераторами тока. Ток I_n (прямой ток), который передаётся из эмиттера в базу и собирается коллектором, описывается выражением

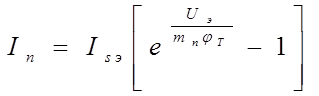,                                  (2.28)

где   I_sэ – ток насыщения эмиттерного перехода;

U_э – напряжение перехода эмиттер – база;

m_n – коэффициент не идеальности в нормальном режиме;

j_г – температурный потенциал.

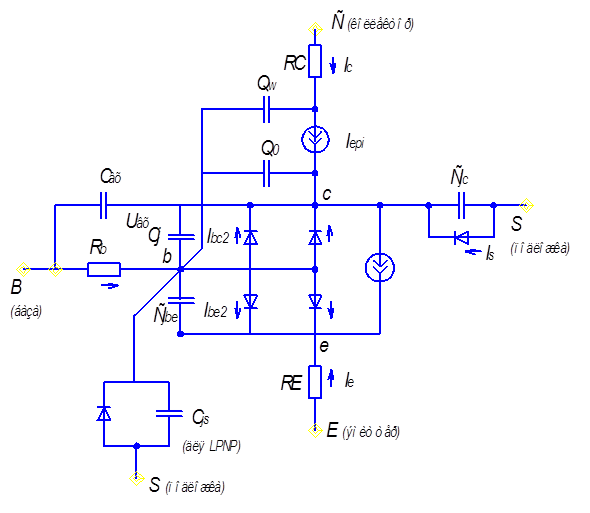
Рисунок 2.16- Эквивалентная схема модели транзистора по Гуммелю- Пунну.

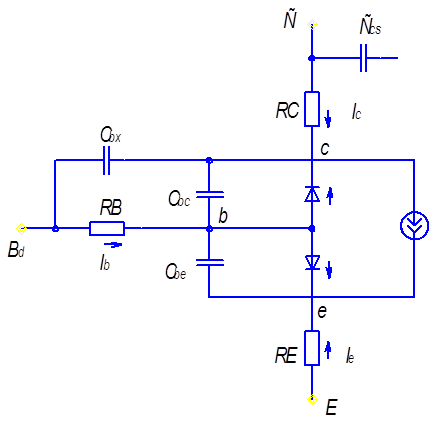
Рисунок. 2.17- Модель транзистора по Эберсу – Моллу.

Аналогично записывается выражение для тока I_i , который передаётся из коллектора через базу в эмиттер в инверсном режиме

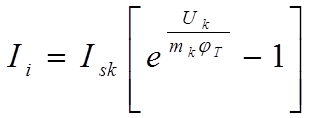,                                  (2.29)

где   I_sк – ток насыщения коллекторного перехода;

U_к – напряжение перехода коллектор – база;

m_к – коэффициент не идеальности перехода коллектор – база в нормальном режиме;

j_Т – температурный потенциал.

В цепь базы транзистора ответвляется ток

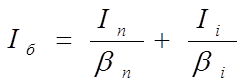,                                       (2.30)

где I_б – ток базы;

b_n, b_i – прямой и обратный коэффициенты передачи соответственно.

Диффузионные ёмкости  С_{э диф} эмиттерного и С_{к диф} коллекторного переходов, согласно рисунок 2.17 подключены параллельно и рассчитываются по формулам 

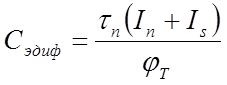,                                     (2.31)

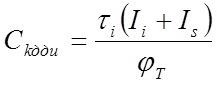,                                      (2.32)

где   t_n, t_i – диффузионные постоянные времени в прямом и инверсном включении.

Постоянные времени t_n и t_i характеризуют инерционность процессов передачи зарядов не основных носителей от одного перехода к другому. Барьерная ёмкость не линейно зависит от обратного напряжения перехода и приближённо описывается выражением

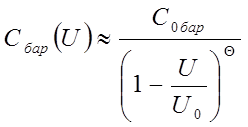,                                     (2.33)

где   С_{0 бар} – барьерная ёмкость p-n перехода при нулевом смещении (U=0);

U₀- параметры, определяемые из условия согласования экспериментальной