Квантовая теория
![]()
![]()
![]()
Семестр II
Тема
Теория возмущений
Лекция XVIII
Нестационарная теория возмущений
Как меняются состояния со временем?
Представление в базисе не возмущенной задачи
![]()
?
I. Представление в базисе невозмущенной задачи
Уравнения в базисе невозмущенной задачи:
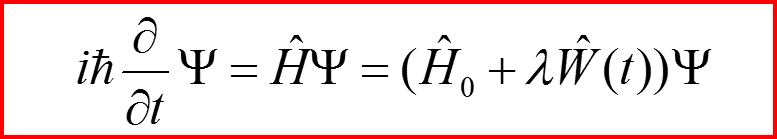
Подставляем разложение Ψ(t) по базису:
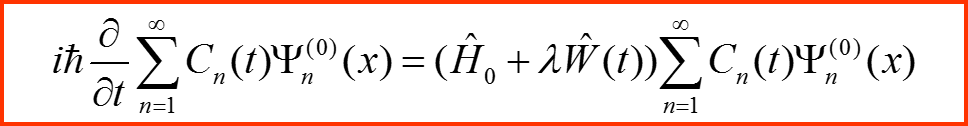
I. Представление в базисе невозмущенной задачи
Проектируем уравнение на базис Ψn(0) :
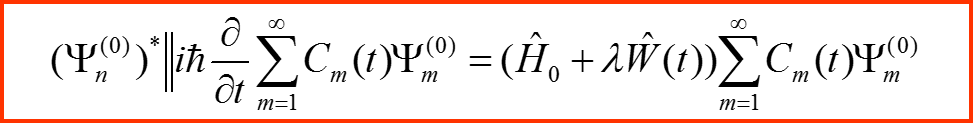
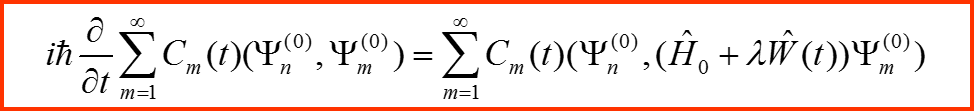
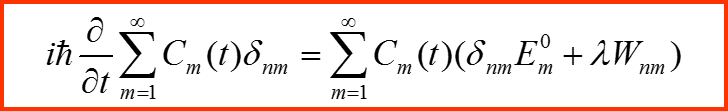
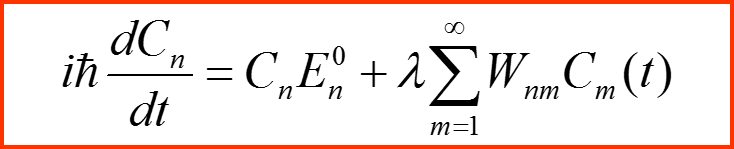
I. Представление в базисе невозмущенной задачи
Разложение решения по малому параметру Λ:
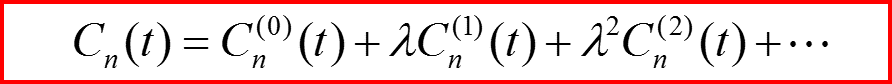
Нулевой порядок разложения:
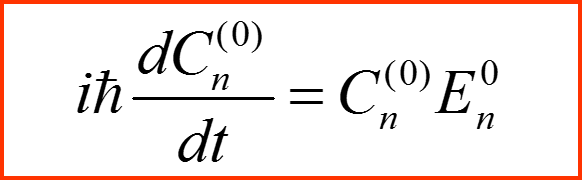
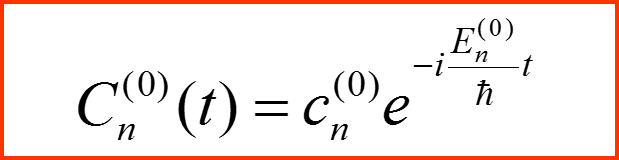
I. Представление в базисе невозмущенной задачи
Следующие порядки разложения:
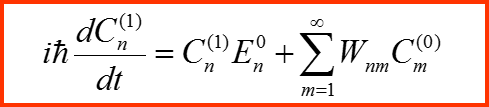
1
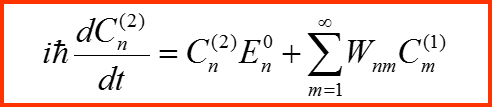
2
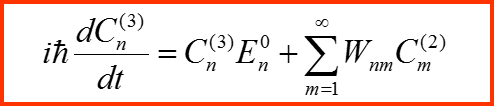
3
I. Представление в базисе невозмущенной задачи
Первый порядок разложения:
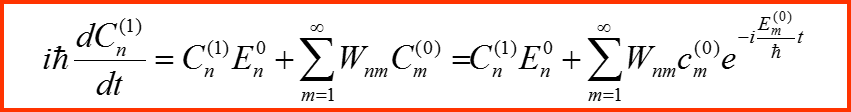
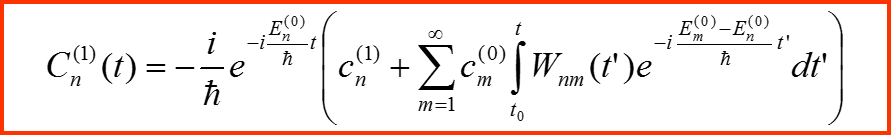
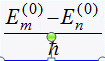
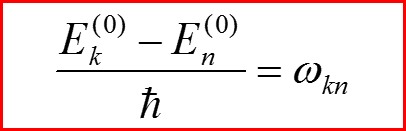
I. Представление в базисе невозмущенной задачи
Частоты Бора:
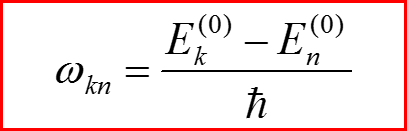
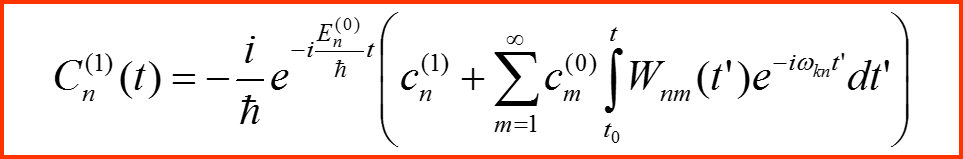
II. Теория квантовых переходов
Рассмотрим задачу о вероятности перехода квантовой системы из одного состояния в другое за некоторое время t с момента начала внешнего воздействия на нее внешнего вынуждающего воздействия, изменяющегося со временем. Будем предполагать, что гамильтониан невозмущенной системы есть H0:
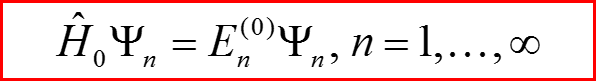
II. Теория квантовых переходов
Полный гамильтониан системы со взаимодействием можно представить в виде:
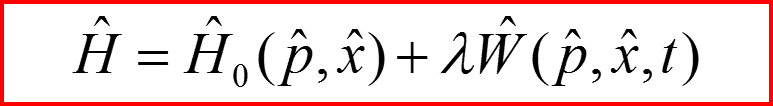
Параметр Λ характеризует интенсивность взаимодействия системы с внешними полями
II. Теория квантовых переходов
Задача состоит в вычислении вероятности Pn->m(t) перехода системы из невозмущенного состояния Ψn(0) с номером n в другое состояние той же невозмущенной системы Ψm(0) . Предполагается, что к моменту измерения нового состояния системы внешнее воздействие закончилось.
II. Теория квантовых переходов
Считая параметр Λ (Λ <<1) малым, искать решение будем в виде разложения по этому параметру.
Волновую функцию системы Ψ(n)(x,t) в момент времени t, при условии: Ψ(n)(x,0) = Ψn (0)(x) разложим в ряд по Λ.
II. Теория квантовых переходов
Процедура вычисления вероятностей:
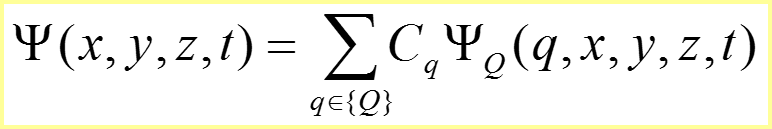
1
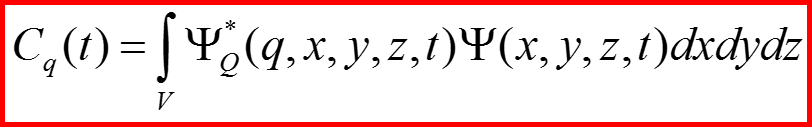
2
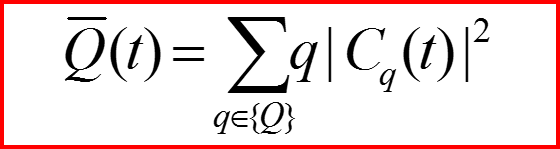
3
II. Теория квантовых переходов
Вероятность перехода из невозмущенного состояния можно вычислить с помощью формулы:
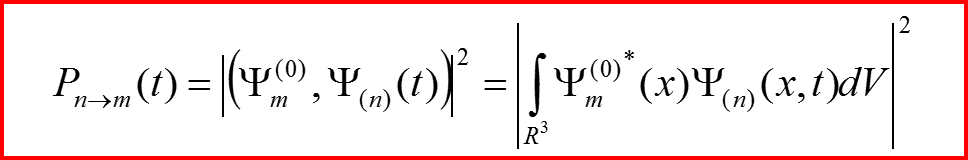
II. Теория квантовых переходов
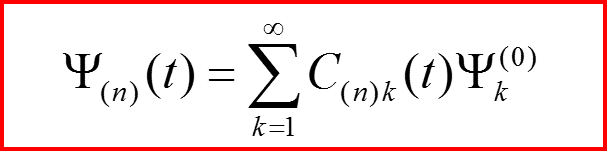
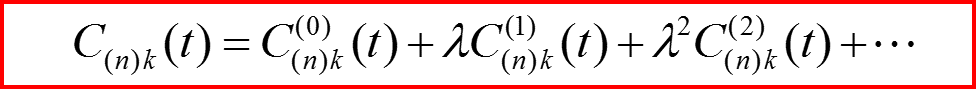
Из начального условия Ψ(n)(x,0) = Ψn (0)(x) следует:

III. Первый порядок теории возмущений
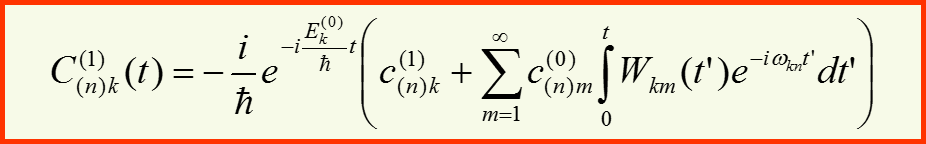

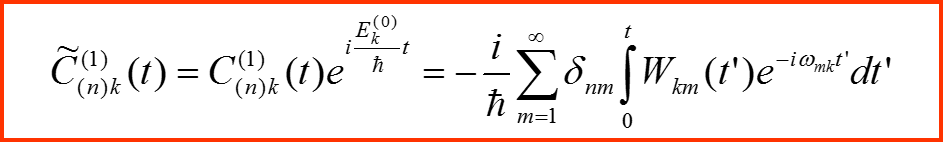
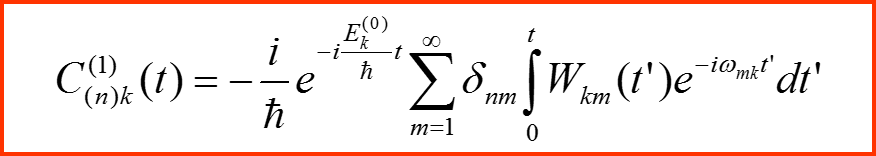
III. Первый порядок теории возмущений
В результате находим:
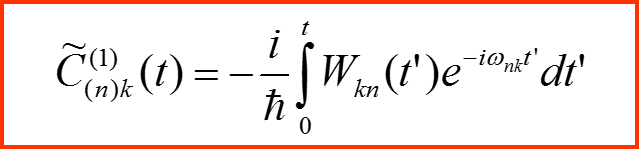
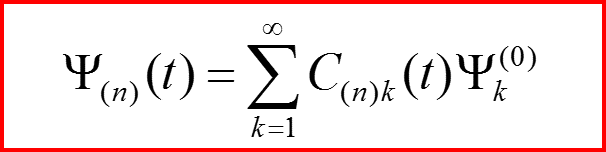
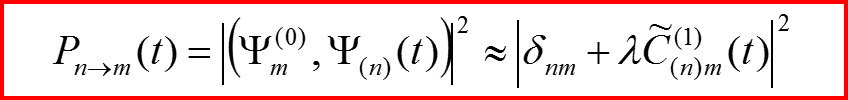
III. Первый порядок теории возмущений
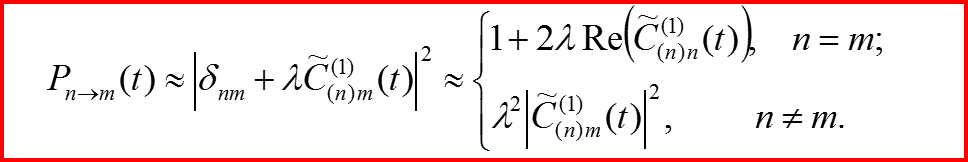
Для вероятностей перехода (т≠n):
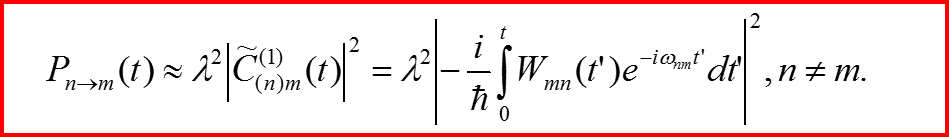
III. Первый порядок теории возмущений
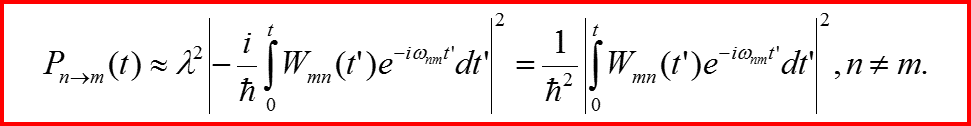
Переход к Фурье-компонентам! Пусть выполнено условие:
Это почти Фурье-преобразование!
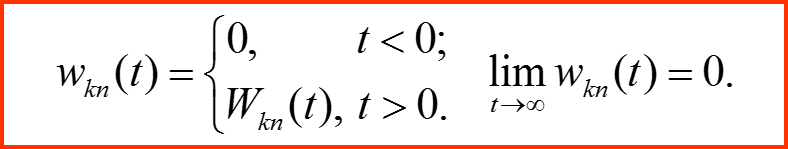
III. Первый порядок теории возмущений
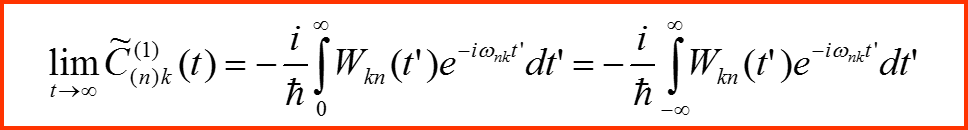
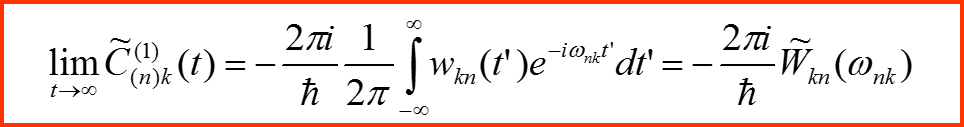
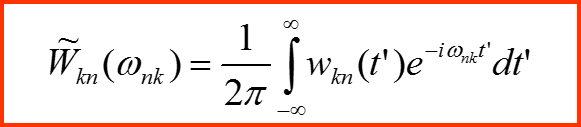
III. Первый порядок теории возмущений
Окончательная формула для вероятностей перехода (т≠n):
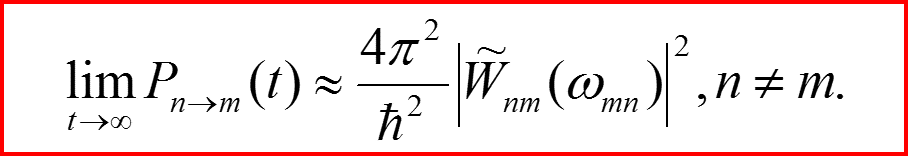
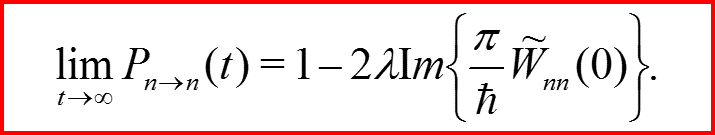
III. Первый порядок теории возмущений
Основные результаты:
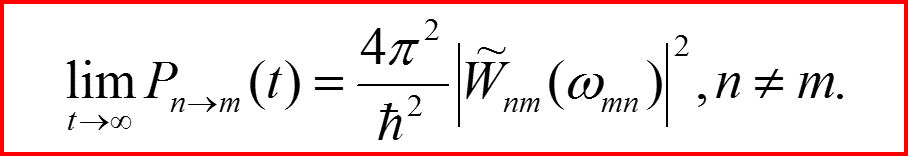
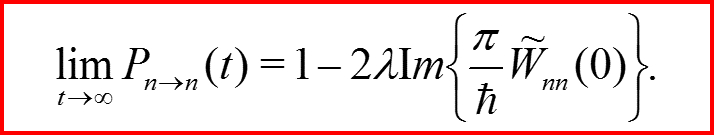
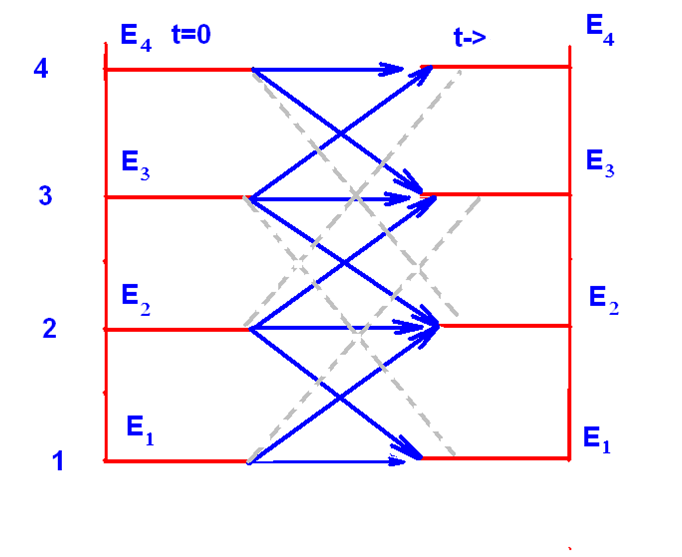
Правила отбора
![]()
Как симметрии проявляются в вероятностях перехода?
IV. Правила отбора Общее определение
Правилом отбора называются условия позволяющие установить возможность перехода с одного уровня на другой под действием внешнего возмущения с ненулевой вероятностью. Наличие запрещенных для перехода уровней связано с наличием симметрий в системе.
IV. Правила отбора Пример 1
Пример 1. Рассмотрим заряженный гармонический осциллятор, находящийся во внешнем электрическом поле с напряженностью E(t), изменяющейся со временем
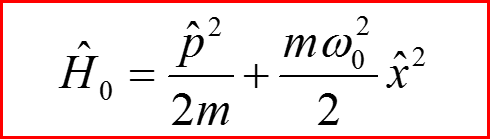
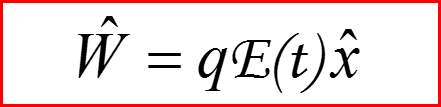
II. Повышающий и понижающий операторы
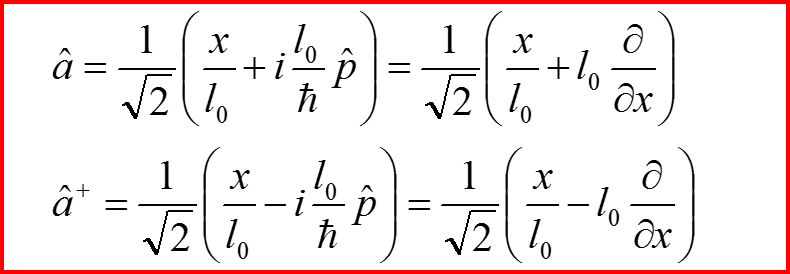
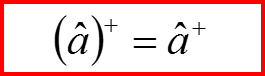
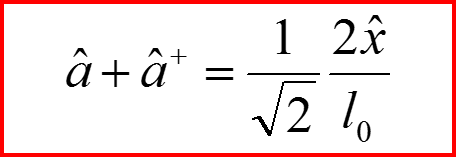
II. Повышающий и понижающий операторы
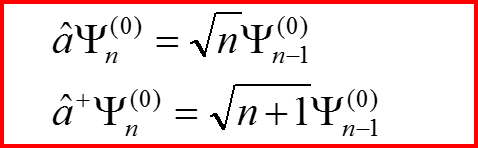
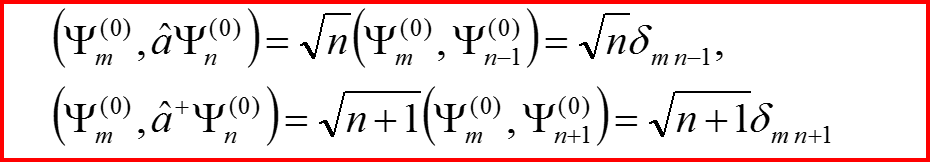
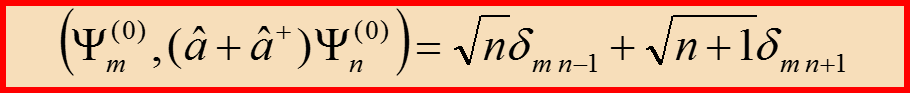
IV. Правила отбора Пример 1
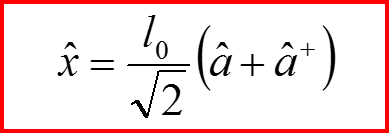
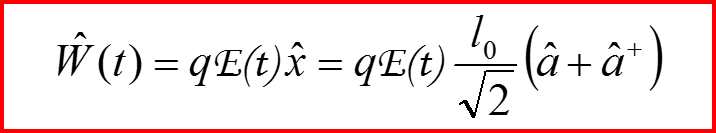
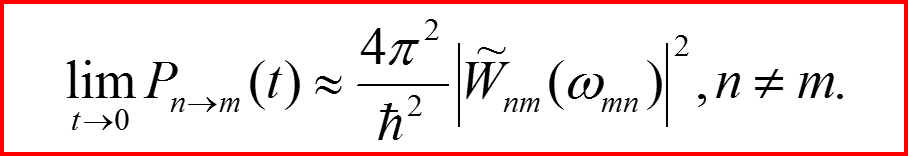
IV. Правила отбора Пример 1
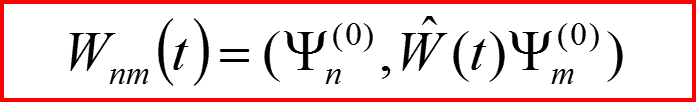
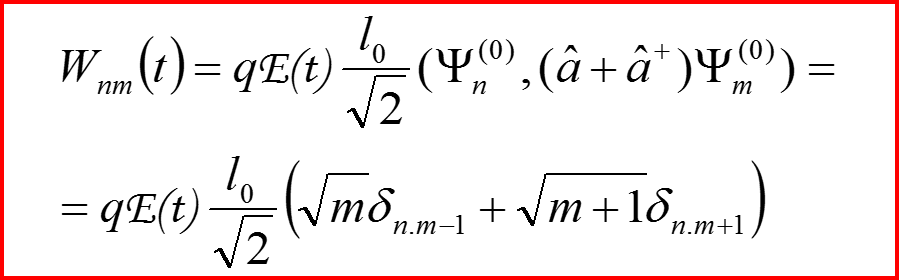
IV. Правила отбора Пример 1
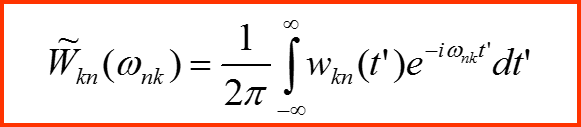
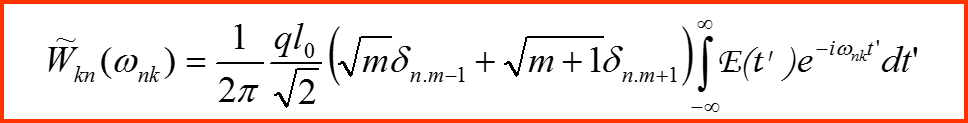
Что это за величина?
IV. Правила отбора Пример 1
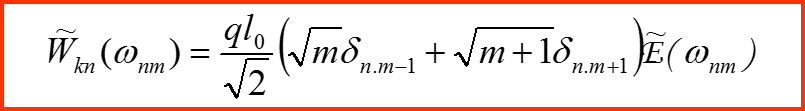
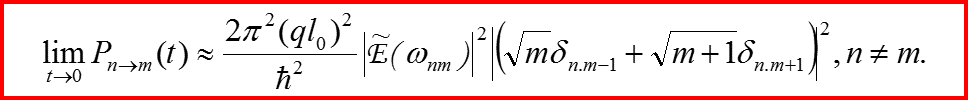
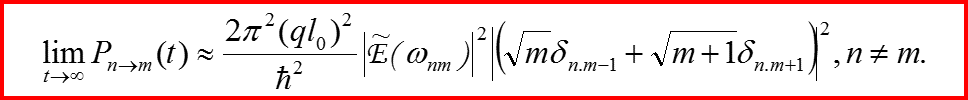
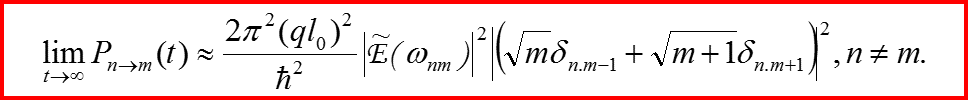
![]()
Теория излучения и поглощения электромагнитного поля
![]()
Как атомы излучаю и поглощают?
V. Теория излучения. Общая постановка задачи
Постановка задачи:
![]()
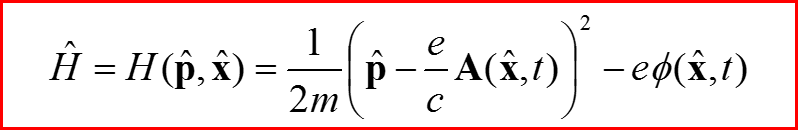
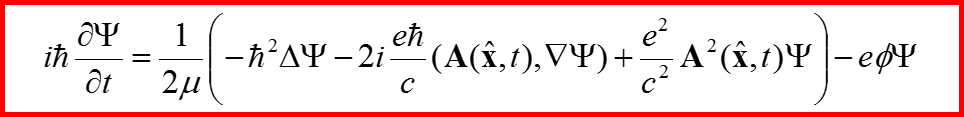
V. Теория излучения
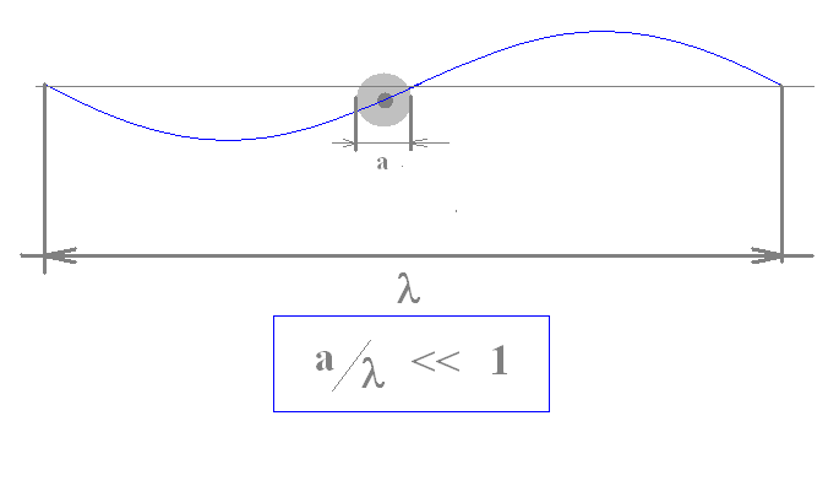
Дипольное приближение:

Точная теория:
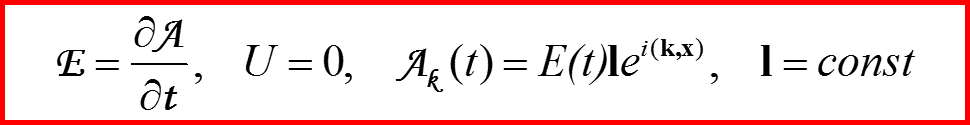
V. Теория излучения. Дипольное приближение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.