Теория представлений. Уравнение Гейзенберга. Базис в гильбертовом пространстве

Квантовая теория

Семестр I

Лекция XIV

Теория представлений. Уравнение Гейзенберга

Как преобразуются операторы, когда в гильбертовом пространстве изменяется базис?

Базис в гильбертовом пространстве

Как выбираются базисы в гильбертовом пространстве?

I. Волновые функции как вектора в гильбертовом пространстве

A) На множестве волновых функций {Ψ} определены две операции – сложение и умножение на комплексное число. Это делает это множество линейным векторным пространством.

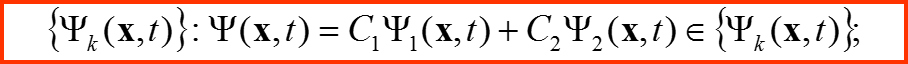
I. Волновые функции как вектора в гильбертовом пространстве

Б) На множестве волновых функций {Ψ} определена операция скалярного умножения: (Ψ1,Ψ2)=ſ Ψ*1 Ψ2dV Это делает это множество линейным эрмитовым векторным пространством. Это пространство называется гильбертовым

I. Волновые функции как вектора в гильбертовом пространстве

Набор функций (бесконечный) {Ψk} такой, что

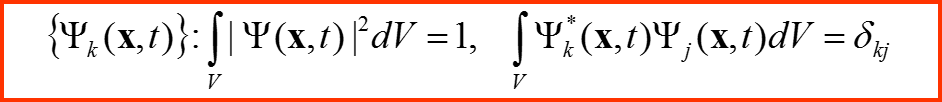
Называется ортонормированным базисом гильбертова пространства

I. Волновые функции как вектора в гильбертовом пространстве

Естественными ортонормированными базисами гильбертова пространства являются собственные функции динамических операторов!

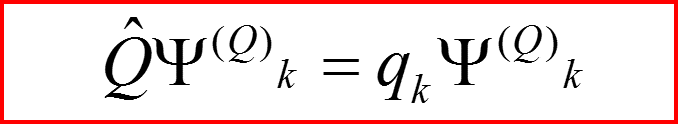
II. Матричное представление операторов

Что означает выбрать базис в гильбертовом пространстве?

Пусть имеются два базиса:

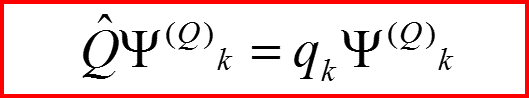
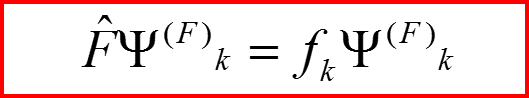
II. Матричное представление операторов

Функции двух аргументов k и t

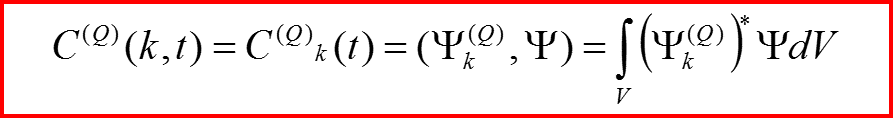
Или волновыми функциями в представлениях операторов Q и F

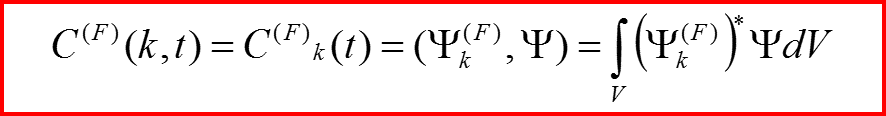
называются волновой функцией системы в базисах базисаx {Ψ(Q)} и {Ψ(F)}

II. Матричное представление операторов

Величины

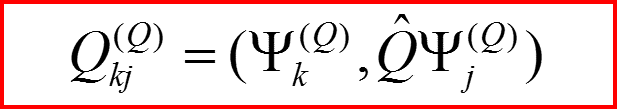
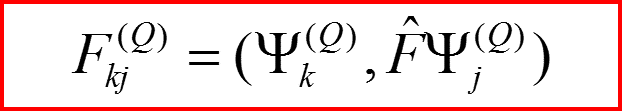
Называются матричными элементами операторов Q и F в представлении Q.

II. Матричное представление операторов

Величины

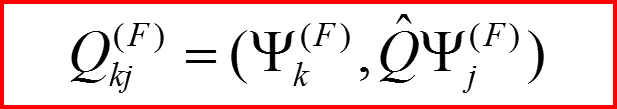
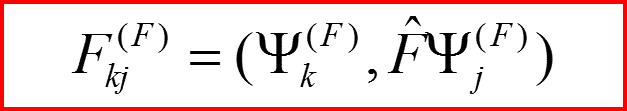
называются матричными элементами операторов Q и F в представлении Q.

II. Матричное представление операторов

Из определения следует:

Примеры

Энергетическое и импульсное представления

III. Энергетическое представление

Пусть Ψk – полный набор стационарных состояний

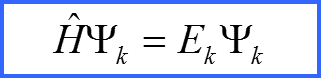
Тогда уравнение Шредингера в энергетическом представлении имеет вид

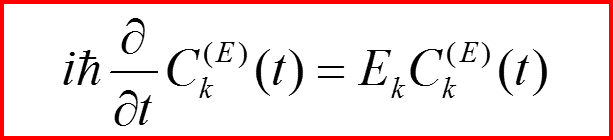
III. Энергетическое представление

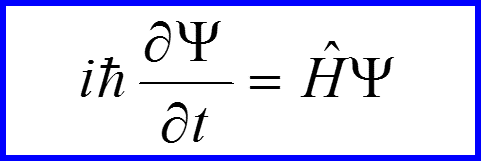
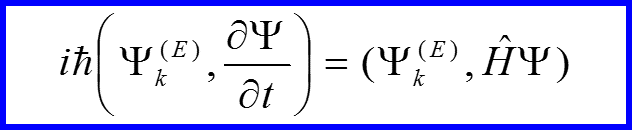
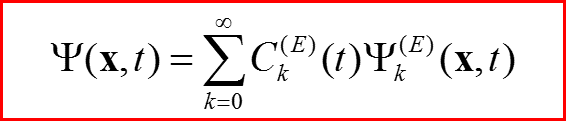
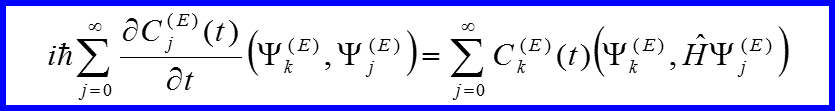
III. Энергетическое представление

В результате имеем:

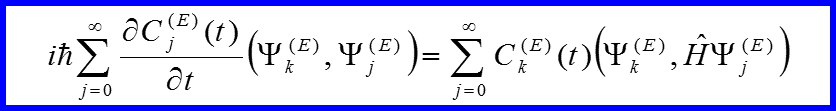
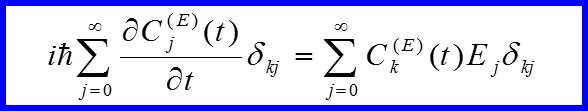
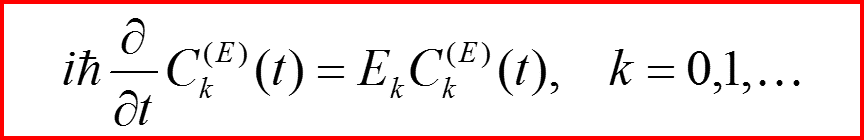
III. Импульсное представление

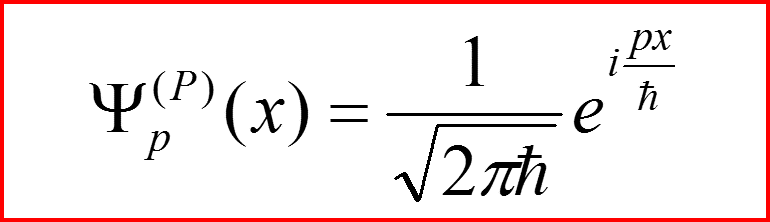
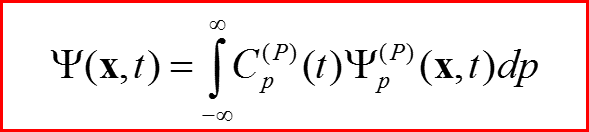
III. Импульсное представление

Уравнение Шредингера для импульсного представления

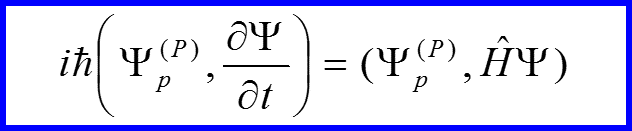
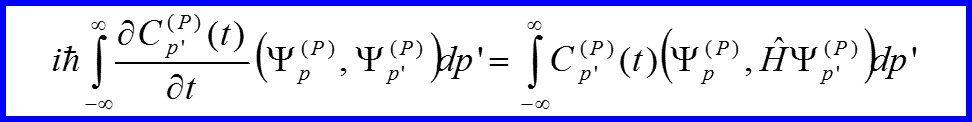
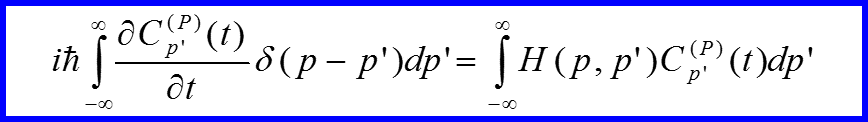
III. Импульсное представление

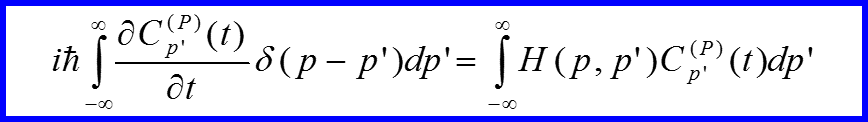
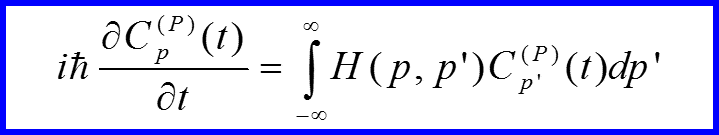
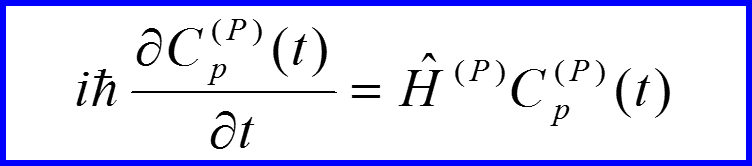
Преобразования от одного базиса к другому

Унитарные операторы

IV. Унитарные операторы

Матрица U преобразования от одного представления (базиса) к другому:

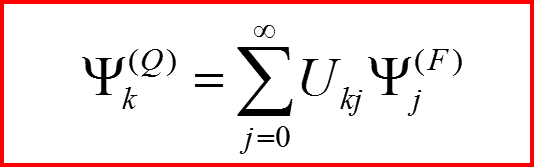
является унитарной

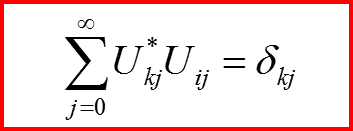
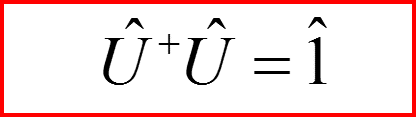
IV. Унитарные операторы

При переходе от одного представления (базиса) к другому матричные элементы операторов преобразуются по формулам:

IV. Унитарные операторы

При переходе от одного представления (базиса) к другому матричные элементы единичного оператора не меняются. Поэтому

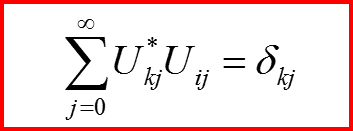
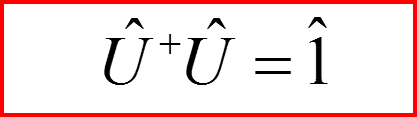
Картина (представление) Гейзенберга

Оператор эволюции

V. Оператор эволюции

Формальное операторное решение уравнения Шредингера для случая

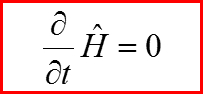
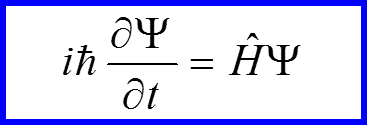
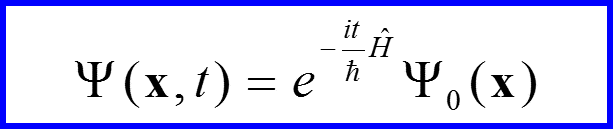
V. Оператор эволюции

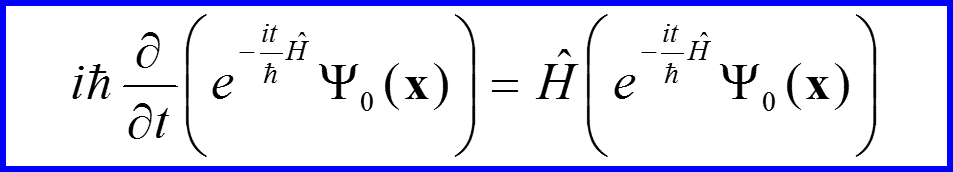
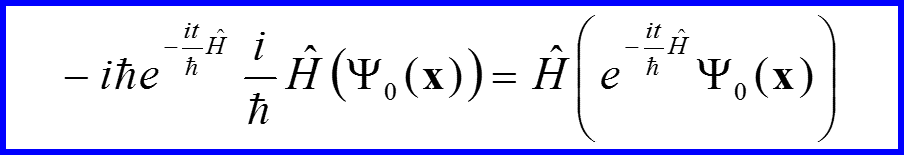
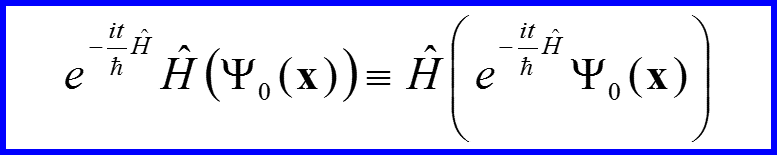
V. Оператор эволюции

Унитарный оператор

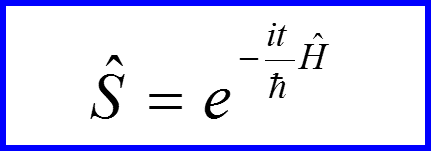
называется оператором эволюции

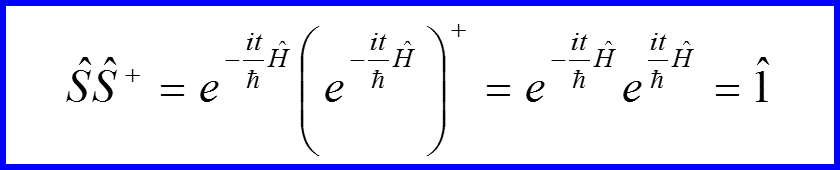
V. Представление Гейзенберга

Оператор

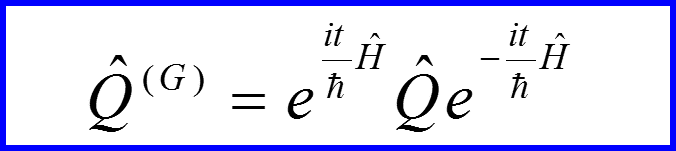
соответствующий оператору Q, называется оператором в представлении Гейзенберга

V. Представление Гейзенберга

Оператор Гамильтона в гейзенберговском представлении

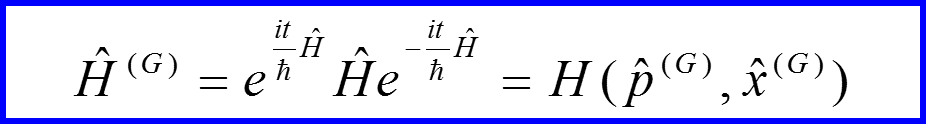
Волновая функция

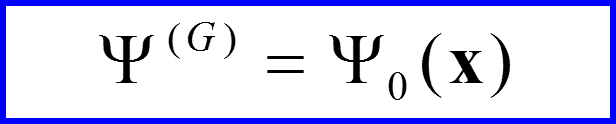
V. Уравнение Гейзенберга

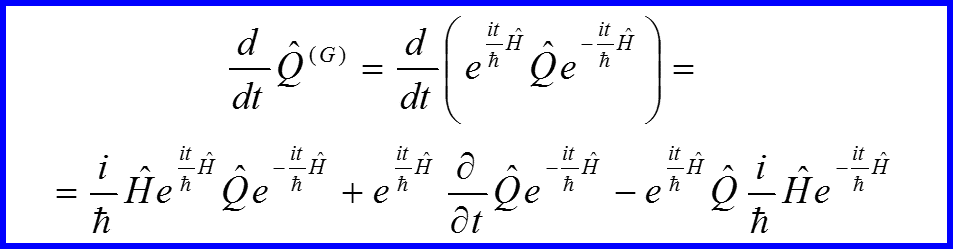
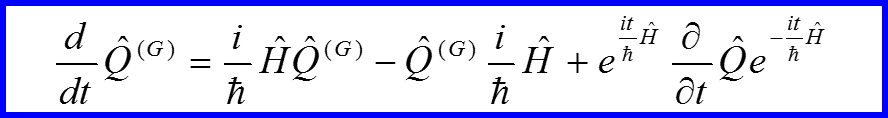
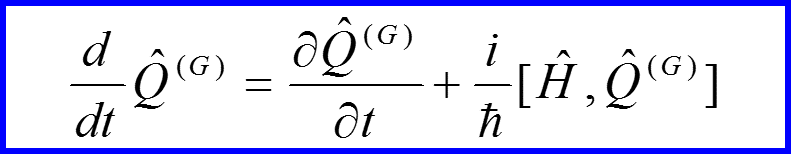
V. Уравнение Гейзенберга

Уравнение

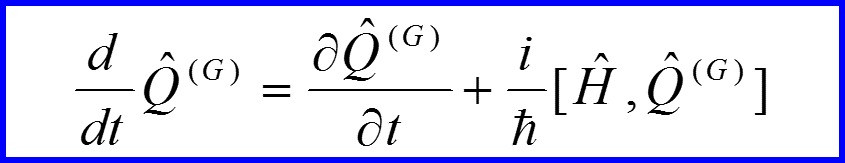
называется уравнением Гейзенберга

V. Уравнение Гейзенберга

Пример

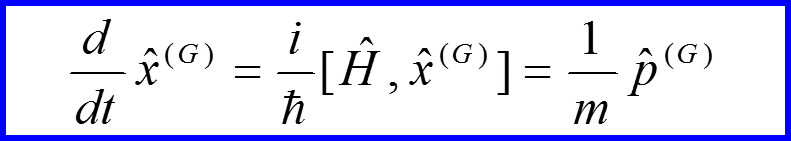
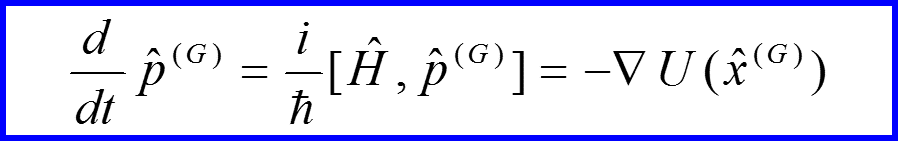
V. Уравнение Гейзенберга

Пример. Гармонический осциллятор

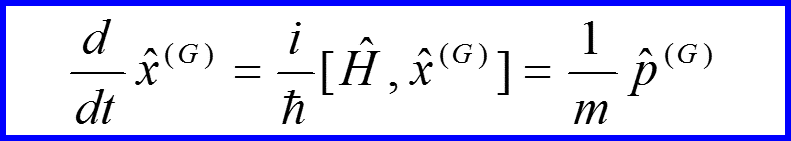
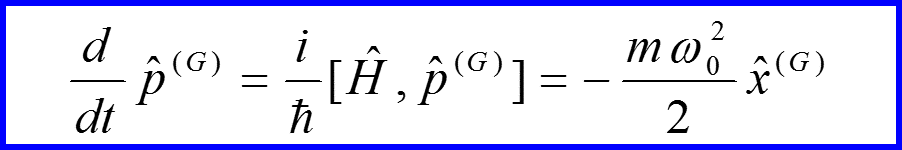
S-матрица

V. S-матрица

Оператор

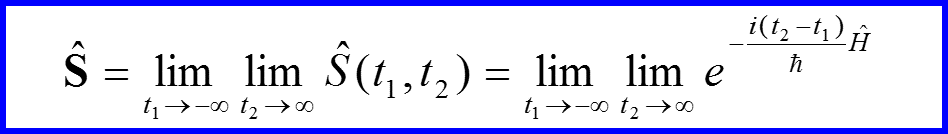
называется S-матрицей. Этот оператор переводит состояния при t-> -∞ в состояния при t->∞

Следующая лекция

Общие вопросы квантовой механики