Квантовая теория
![]()
![]()
![]()
Семестр II
Тема
Лекция XVIII
Теория возмущений с вырождением
Как совершаются переходы между уровнями в квантовых системах?
Вырожденные уровни
![]()
Расщепление уровней
I. Вырожденные уровни
Если гамильтониан системы обладает симметрией, то одному значению энергии (уровню) соответствует несколько волновых функций:
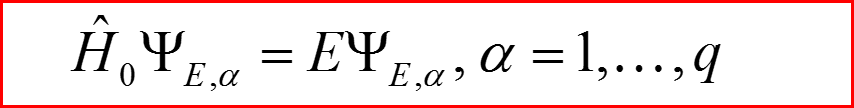
Целое число q называется кратностью вырождения
II.1 Состояния системы, имеющей вырожденные уровни
Общий вид волновой функции с фиксированной энергией:
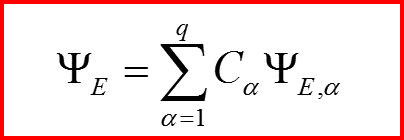
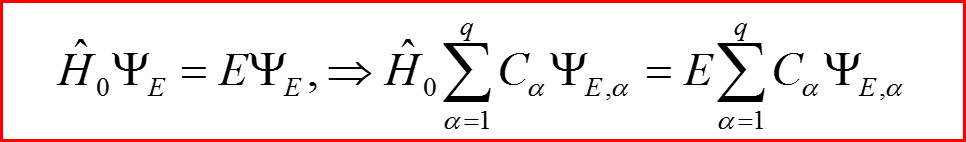
II.1 Состояния системы, имеющей вырожденные уровни
Пример. Общий вид волновых функций электрона в центральном поле:
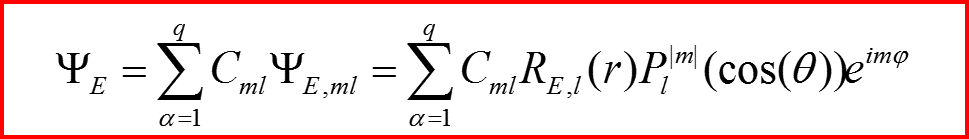
Кратность вырождения q=2l+1
II.2 Снятие вырождения
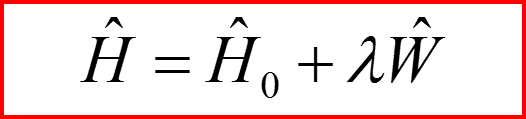
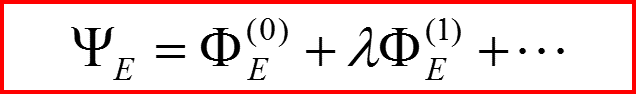
В общем случае происходит снятие вырождения: E(0)→Eα
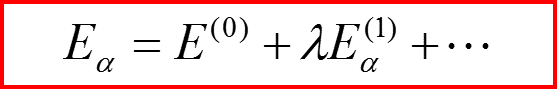
II.2 Снятие вырождения
Снятие вырождения E(0)→Eα означает, что уже в нулевом порядке выбор функции Должен быть произведен с учетом нового номера уровня:
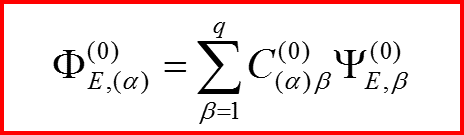
II.3 Представление функций
Общий вид волновой функции в порядке возмущения с номером p:
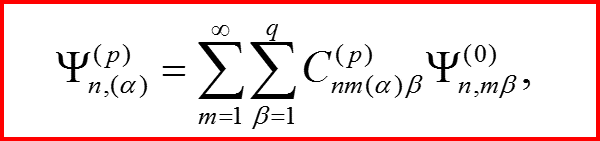
Суммирование ведется и по номерам всех уровней и по индексам вырождения.
II.3 Представление функций
Для нулевого порядка:
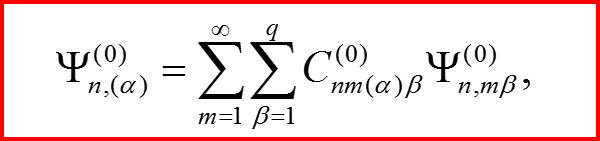
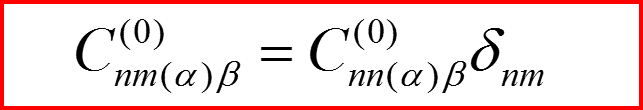
II.3 Уравнения теории возмущений в случае вырождения
Для каждого уровня En, n=1,2,3,…
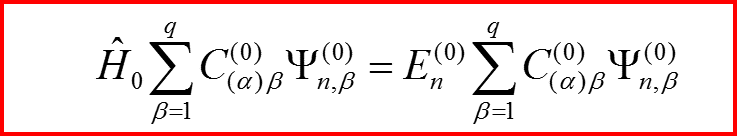
0
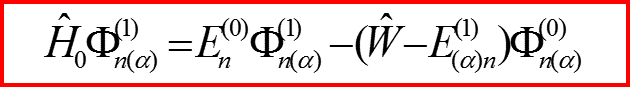
1
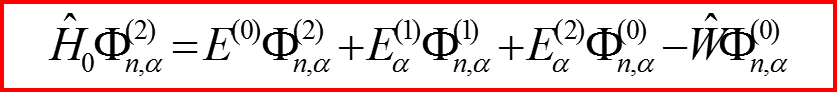
2
II.4 Уравнения в первом порядке
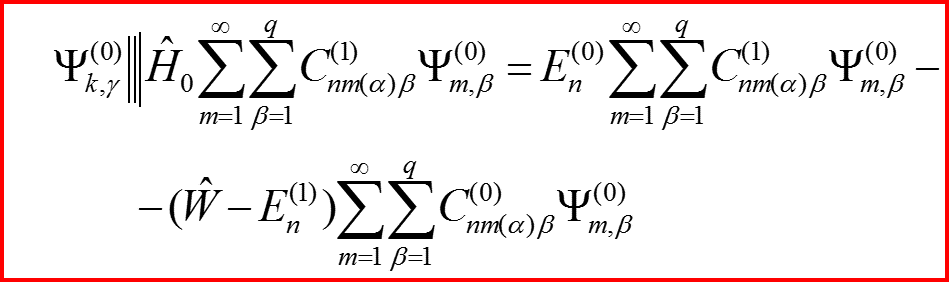
II.4 Уравнения в первом порядке
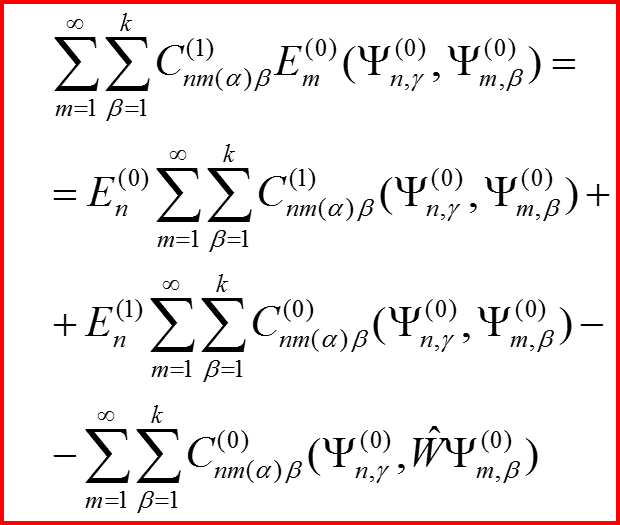
II.4 Уравнения в первом порядке
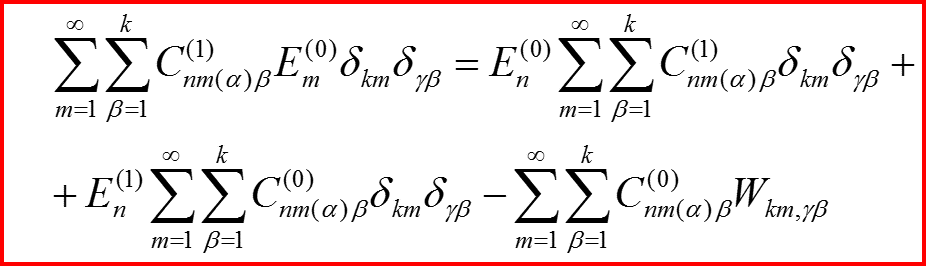
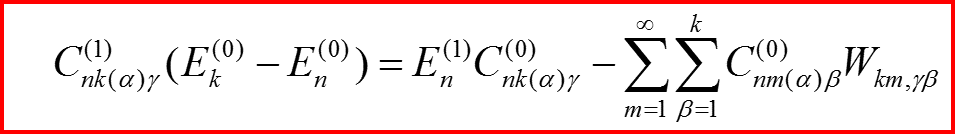
II.4 Уравнения в первом порядке
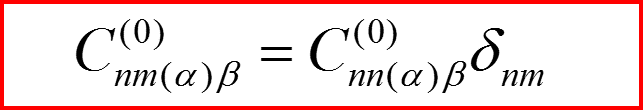
n=k
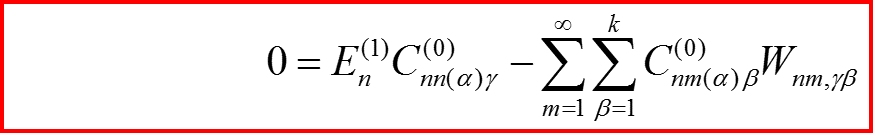
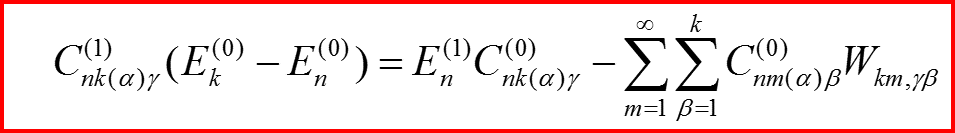
Введем для удобства обозначения:
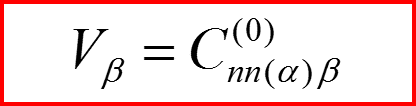
II.4 Уравнения в первом порядке
Уравнения примут вид
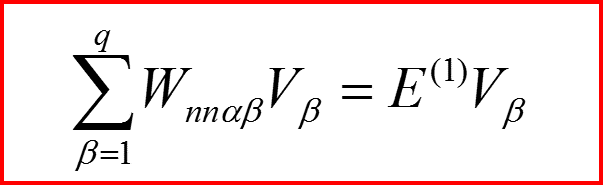
Решения – собственные вектора матрицы Wnn!
II.4 Уравнения в первом порядке
Решения
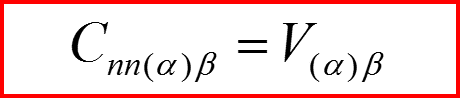
Индекс α – номер собственного вектора!
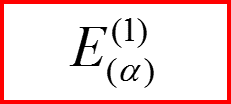
Собственное число
Двукратно вырожденный уровень
![]()
Пример
III. Двукратно вырожденный уровень
Предположим, что рассматриваемый уровень вырожден с кратностью q=2
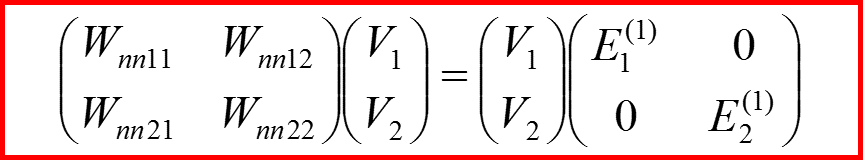
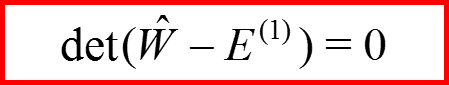
III. Двукратно вырожденный уровень
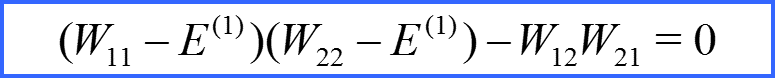
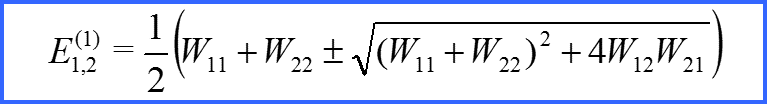

Эффект Штарка
![]()
Расщепление уровней в электрическом поле
IV. Эффект Штарка
Постановка задачи:
![]()
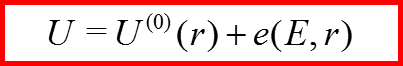
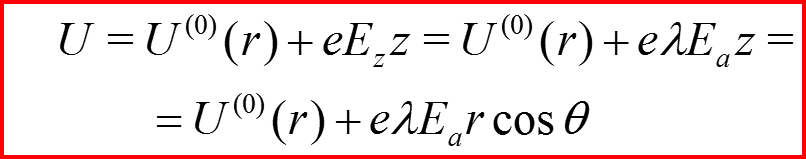
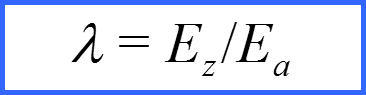
IV. Эффект Штарка
Матричные элементы для l=1
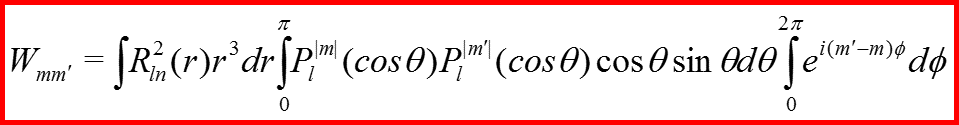
IV. Эффект Штарка для атома водорода
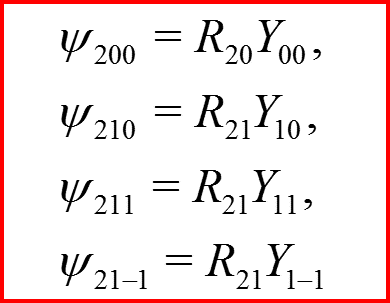
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.