Квазиклассическое приближение. Разложение по малому параметру

Квантовая теория

Семестр I

Лекция XV

Квазиклассическое приближение

На сколько близки классическая и квантовая картины механики?

Разложение по малому параметру

Что такое малый параметр?

I. Общий метод малого параметра

Классическая физика

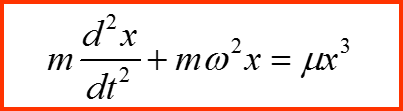
При каких условиях правую часть можно считать малой добавкой? Для ответа на этот вопрос уравнение необходимо оберазмерить!!

I. Общий метод малого параметра

Обезразмеривание – это процедура приведения всех параметров задачи к выбранным стандартным масштабам:

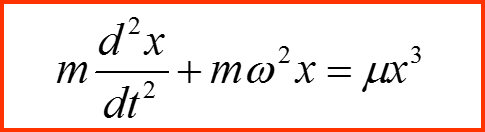
Пусть величины x0 и t0 являются некоторыми стандартными масштабами

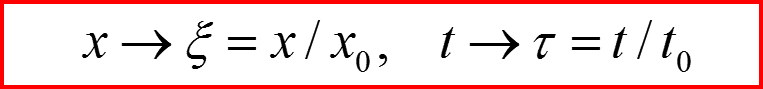
I. Общий метод малого параметра

Переменные ξ и τ называются безразмерными переменными. Уравнение, представленное в безразмерных переменных содержит исключительно безразмерные коэффициенты и называется обезразмеренным:

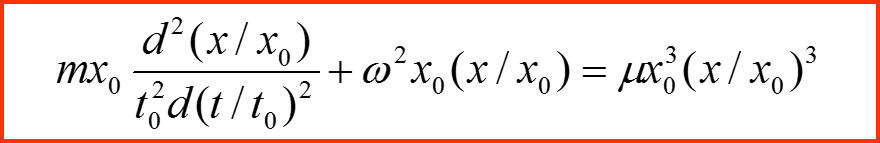
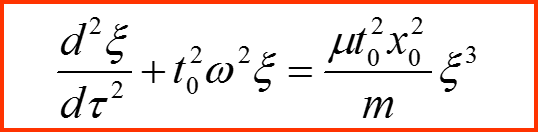
I. Общий метод малого параметра

Постоянные Ω и q являются безразмерными:

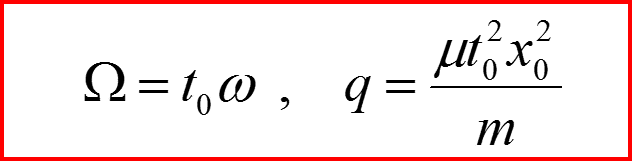
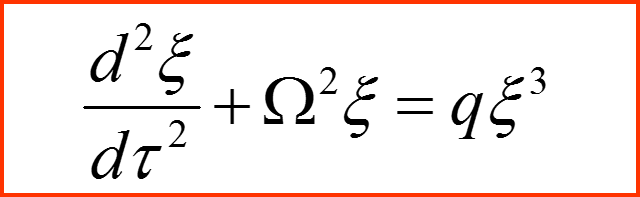
I. Общий метод малого параметра

Для безразмерных параметров неравенство: q<<1 имеет абсолютный смысл. Физический смысл:

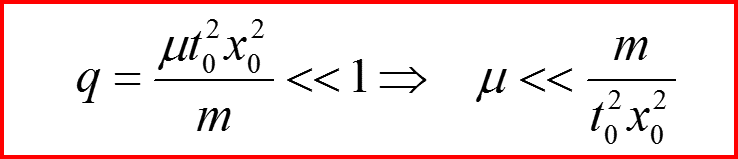
I. Общий метод малого параметра

Разложение решения по малому параметру:

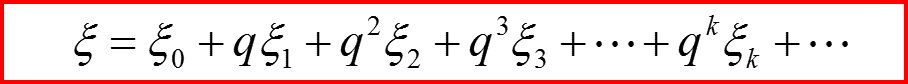
Нулевой порядок приближения (разложения):

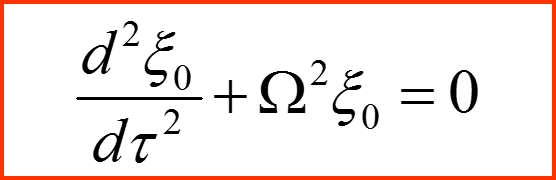
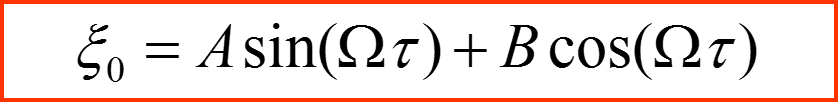
I. Общий метод малого параметра

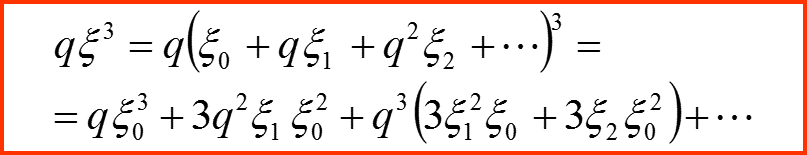
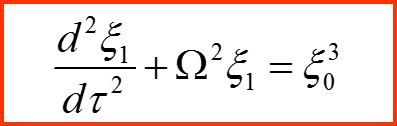
1

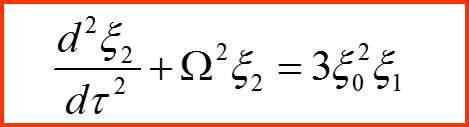
2

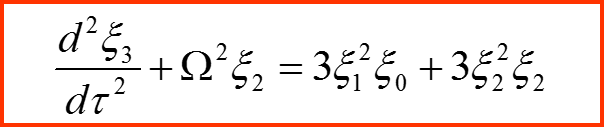
3

I. Общий метод малого параметра

На каждом шаге метода малого параметра решается линейное уравнение!

Совершенно аналогично такой метод может быть применен и к уравнению Шредингера!

Квазиклассическое приближение

Когда постоянная Планка мала?

II. Квазиклассическое приближение

Рассмотрим стационарное уравнение Шредингера:

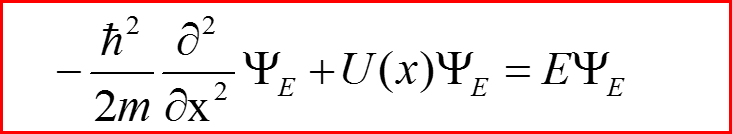
Будем искать решение для Ψ в виде

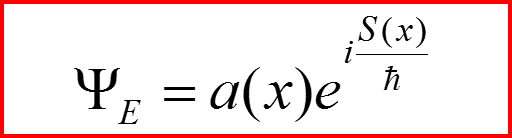
II. Квазиклассическое приближение

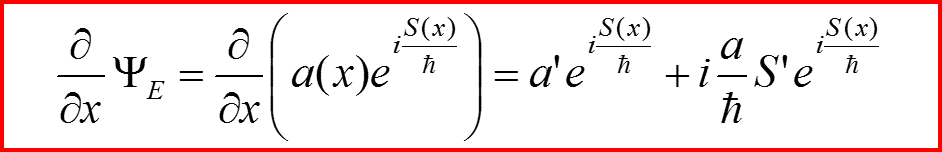
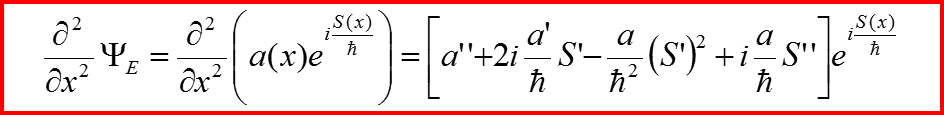
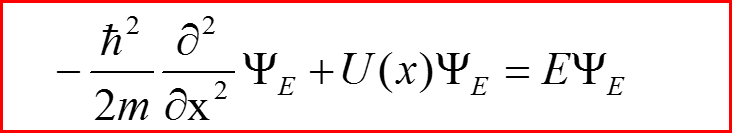
II. Квазиклассическое приближение

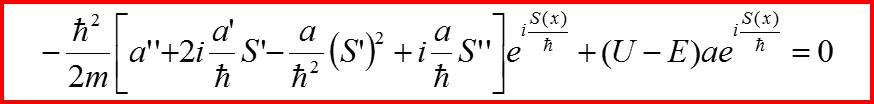
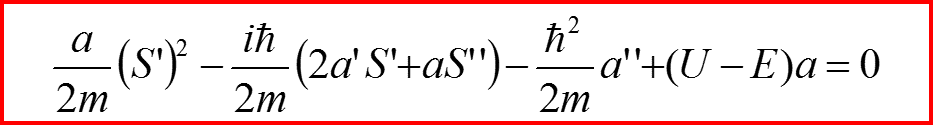
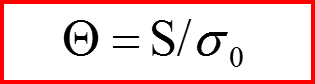
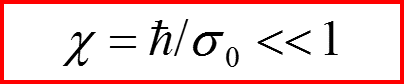
II. Квазиклассическое приближение

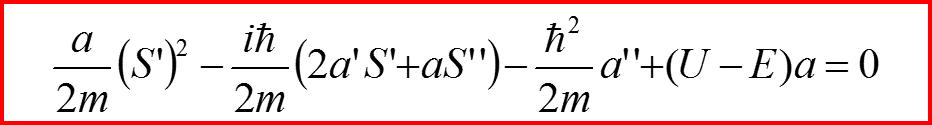
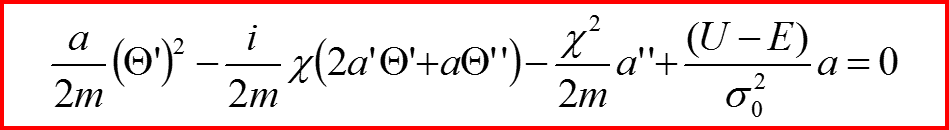
Ищем решение в виде разложения по χ

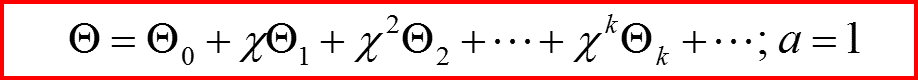
II. Квазиклассическое приближение

В результате имеем:

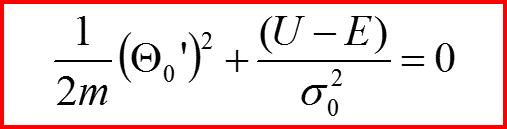
0

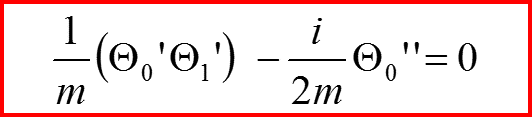
1

II. Квазиклассическое приближение

Нулевой порядок

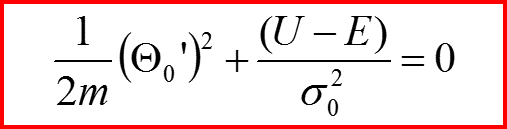
0

Что это за уравнение? ↓

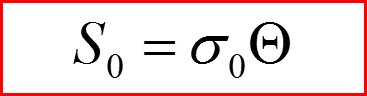
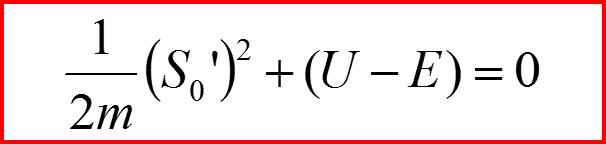
II. Квазиклассическое приближение

Это уравнение Гамильтона-Якоби!

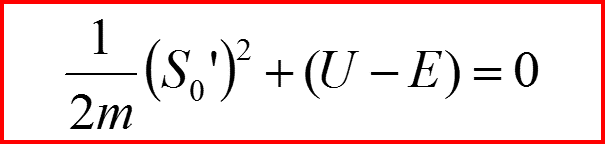
А это – импульс частицы!

А это?

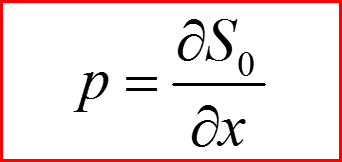
II. Квазиклассическое приближение

Получаем классическое решение задачи о динамике частицы в потенциальном поле:

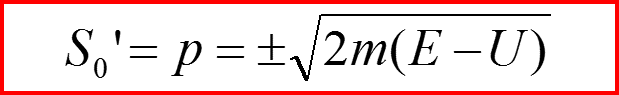
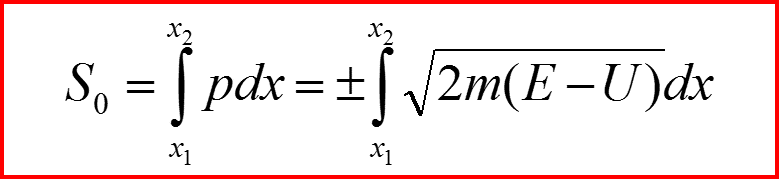
II. Квазиклассическое приближение

Первый порядок

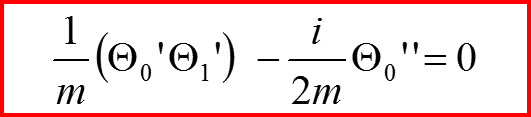
1

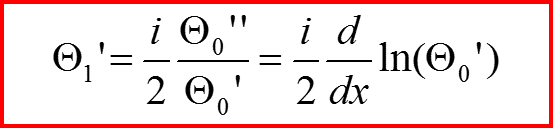
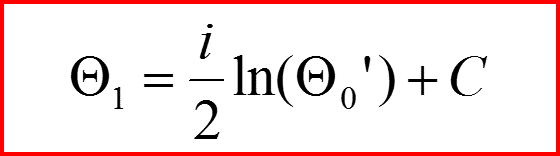
II. Квазиклассическое приближение

Решение в первом порядке

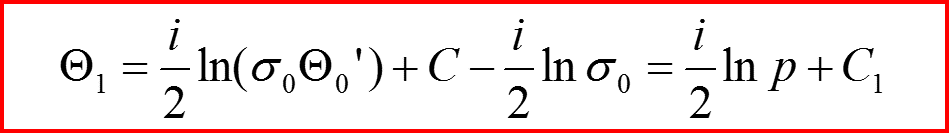
II. Квазиклассическое приближение

Волновая функция в квазиклассическом приближении:

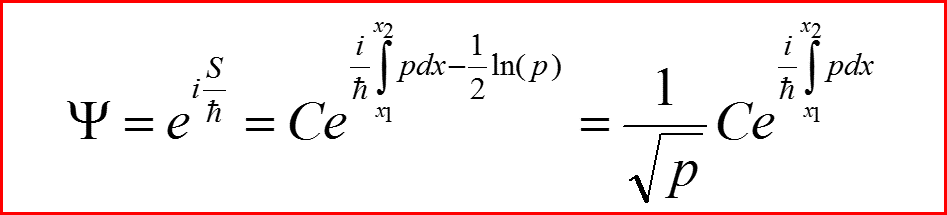
II. Квазиклассическое приближение

Вероятность найти частицу в точке:

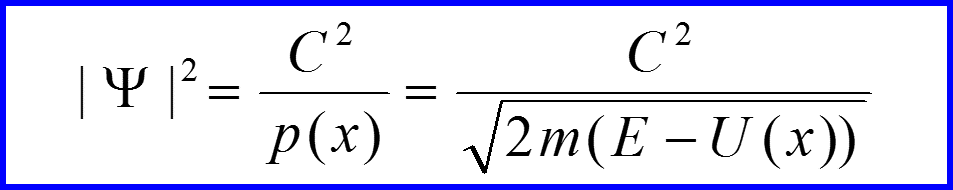
Что это за вероятность?

Где находится классическая частица?

Классическая случайность

III. Классическая вероятность

Рассмотрим задачу о движении классической частицы потенциальной яме

III. Классическая вероятность

Постановка задачи: Наблюдатель случайным образом выбирает момент времени, когда он измеряет положение частицы. Предполагается, что эти моменты времени распределены равномерно на отрезке времени [0,T/2]

III. Классическая вероятность

Какова вероятность того, что частица окажется в точке с координатой x?

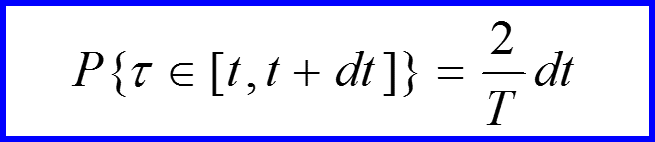
T – период функции

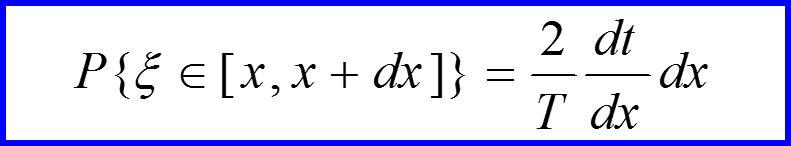
III. Классическая вероятность

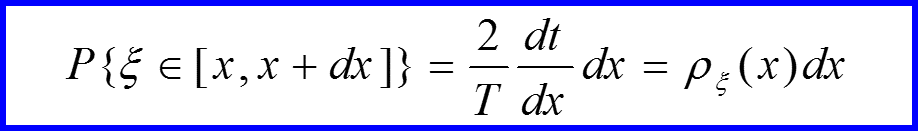
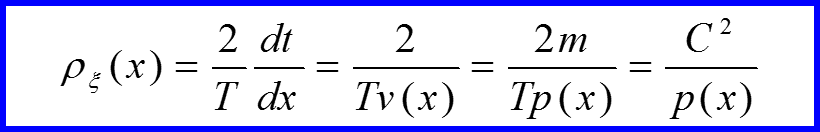
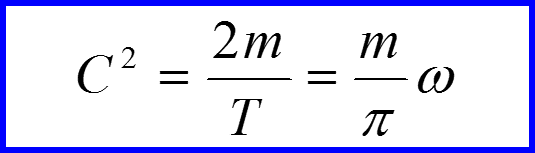
III. Классическая вероятность

Таким образом, квазиклассическое приближение дает решение классической задачи о случайном наблюдении частицы в потенциальной яме!

Является ли это решение хорошим с точки зрения квантовой механики?

Квантование Бора-Зоммерфельда

Как исправить квазиклассическую волновую функцию?

IV. Квантование Бора-Зоммерфельда

Общее квазиклассическое решение

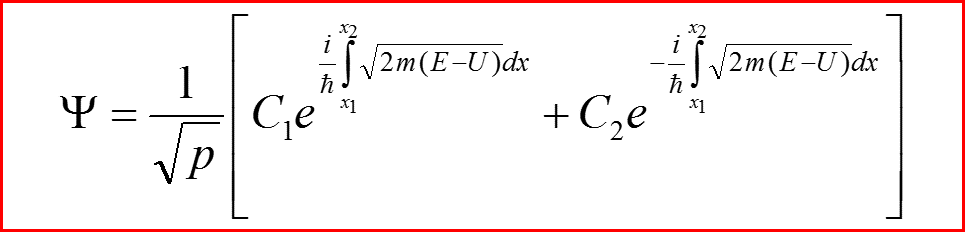
Постоянные C1 и C2 находятся из граничных условий

IV. Квантование Бора-Зоммерфельда

В точке поворота p=0!

Поэтому квазиклассическая волновая функция терпит разрыв в точках поворота!

Можно ли добиться непрерывности квазиклассической волновой функции с помощью граничных условий?

IV. Квантование Бора-Зоммерфельда

Нужно потребовать, что бы в точках поворота функция

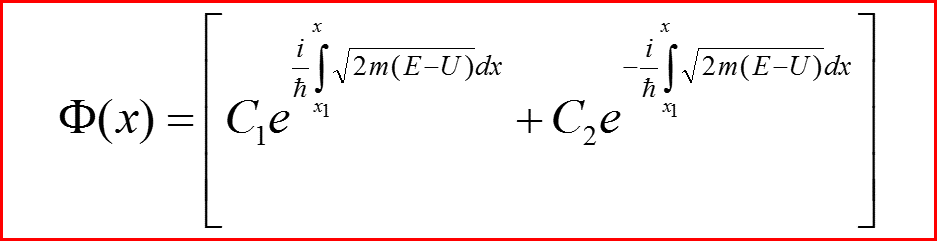
обращалась бы в ноль!

IV. Квантование Бора-Зоммерфельда

Пусть x1 и x2 – точки поворота! Тогда:

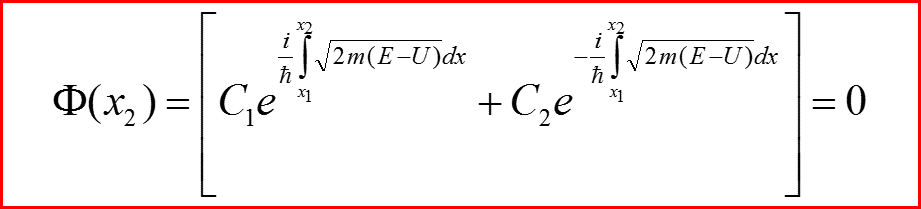
IV. Квантование Бора-Зоммерфельда

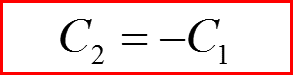
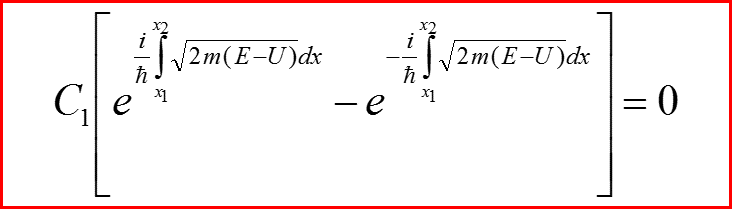
Каков результат?

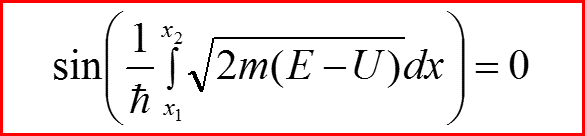
IV. Квантование Бора-Зоммерфельда

Получаем формулу квантования:

Как оказалось, эта формула не работает во всех случаях, кроме атома водорода и гармонического осциллятора!

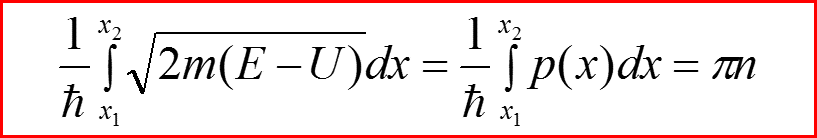
Поэтому квазиклассическое приближение используют только при движении без точек поворота!

Гидродинамическая аналогия

V. Гидродинамическая аналогия

Вернемся к уравнению:

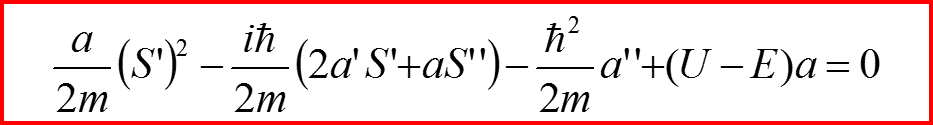
И разделим его на мнимую и действительную части, полагая a и S – вещественными!

V. Гидродинамическая аналогия

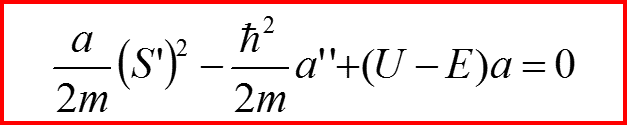
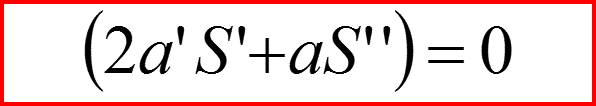
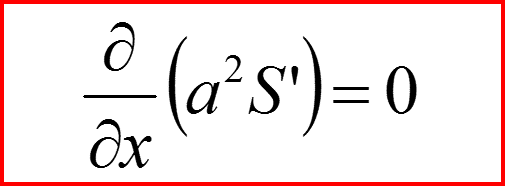
V. Гидродинамическая аналогия

Рассмотрим аналогичное решение нестационарного уравнения Шредингера:

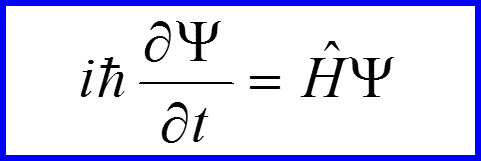
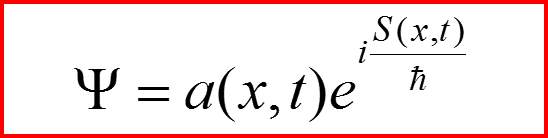
V. Гидродинамическая аналогия

Тогда уравнения для S и a примут вид:

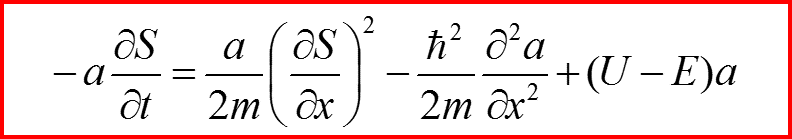
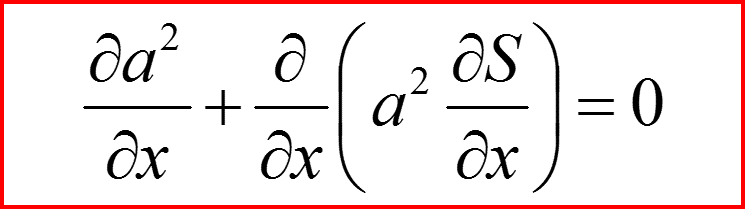
V. Гидродинамическая аналогия

Если ввести обозначения v=Sx /m и ρ=a2 :

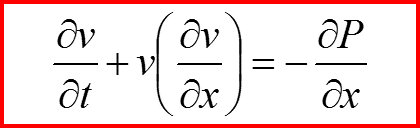
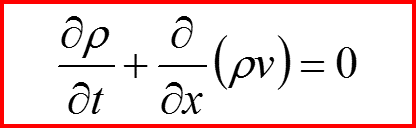
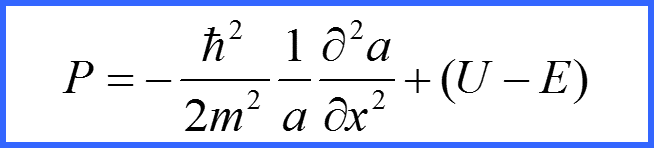
Следующая лекция

Общие вопросы квантовой механики