Квантовая теория
![]()
Семестр I
Лекция IX
Тема: Движение в центральном поле. Оператор момента импульса.
Как устроены волновые функции состояний с фиксированным значением проекций момента импульса?
Уравнение Шредингера в трехмерном пространстве
![]()
Чем существенным отличаются одномерные и многомерные задачи?
I. Оператор Гамильтона для трехмерного движения
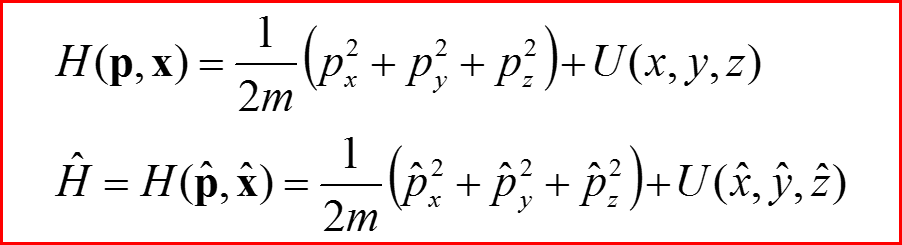
1
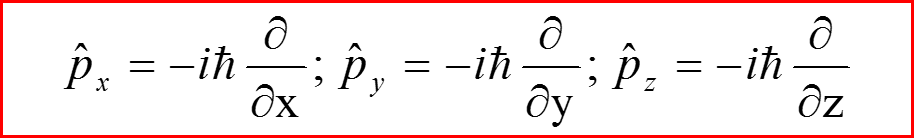
Операторы проекций импульса и координаты:
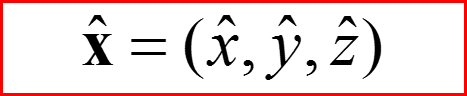
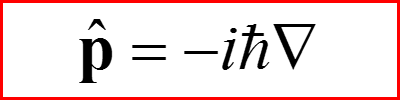
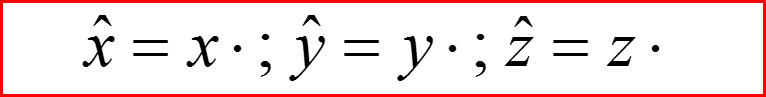
I. Оператор Гамильтона для трехмерного движения
Оператор кинетической энергии:
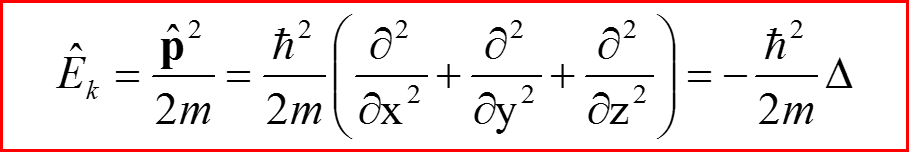
2
Оператор момента импульса:
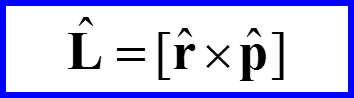
3
IV. Оператор момента импульса
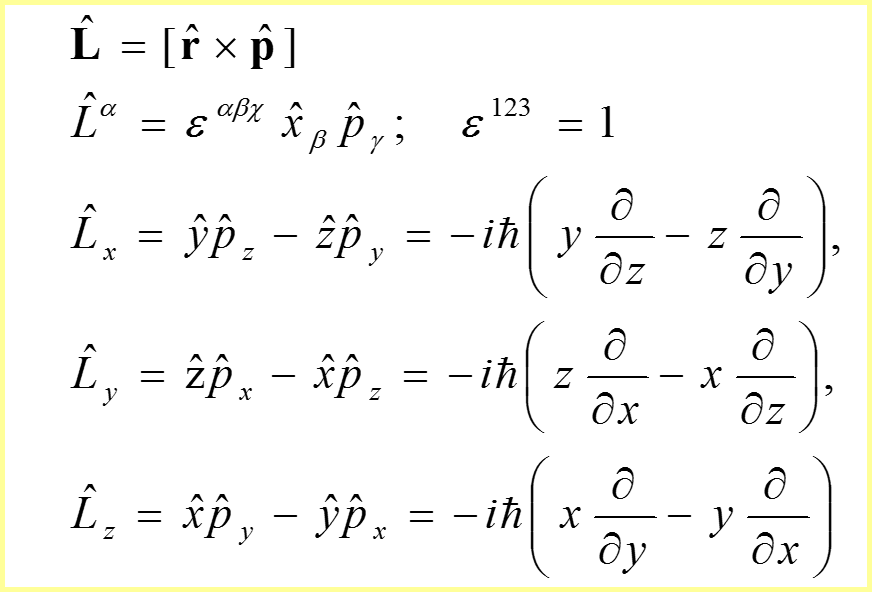
Компоненты оператора момента импульса
4
5
6
II. Уравнение Шредингера для трехмерного движения
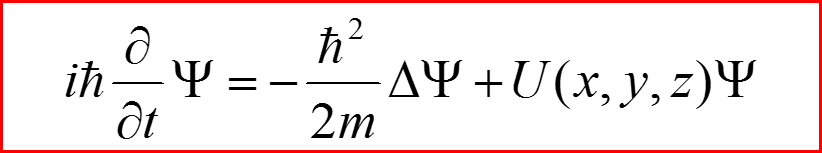
7
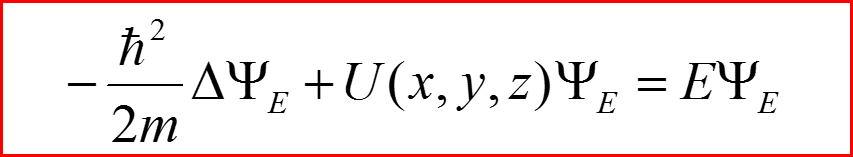
8
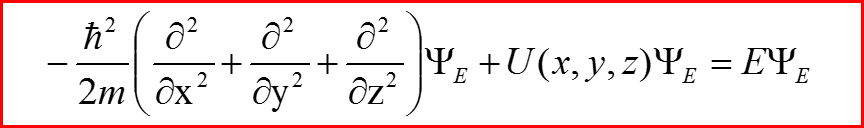
9
II. Уравнение Шредингера для трехмерного движения
Граничные условия!!!
Финитное движение

10
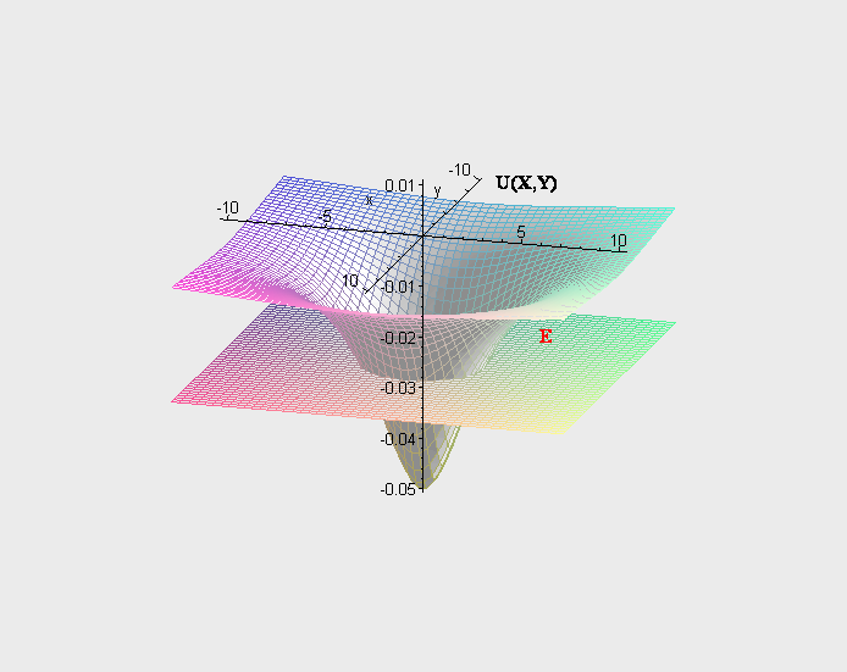
Финитное движение
Финитное движение
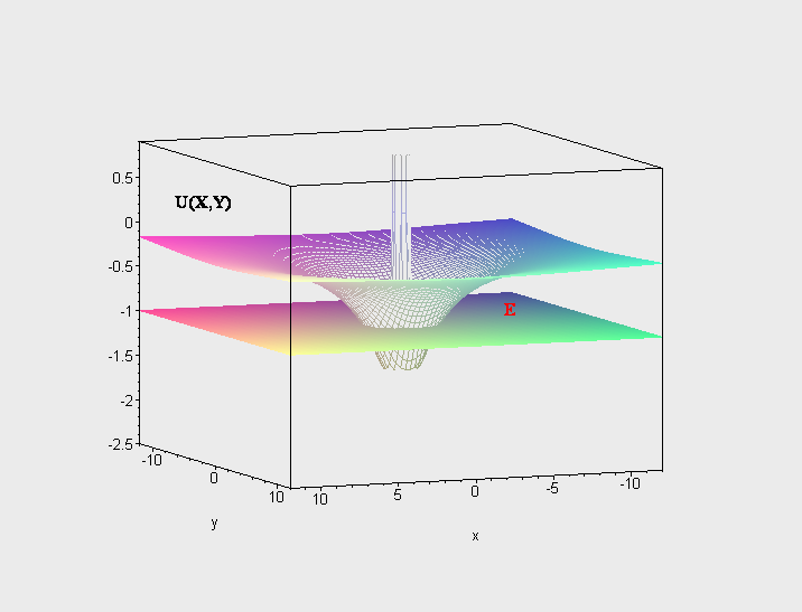
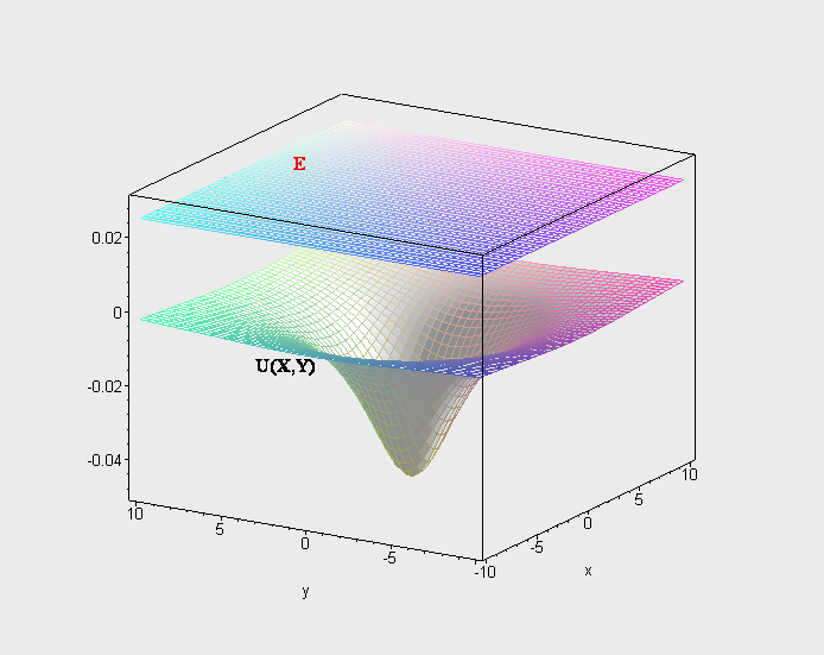
II. Уравнение Шредингера для трехмерного движения
Граничные условия!!!
Инфинитное движение
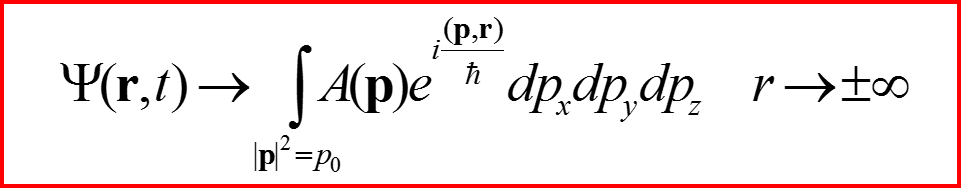
11
Центральное поле
![]()
Законы сохранения для центрального поля
II. Центральное поле
Силовое поле называется центральным, если потенциальная энергия U(r) является функцией только радиального расстояния от точки, называемой центром поля.
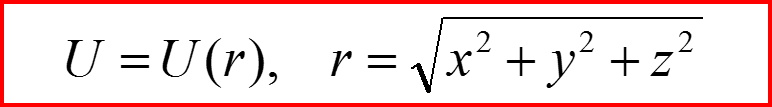
12
II. Операторы Гамильтона и момента импульса для центрального поля
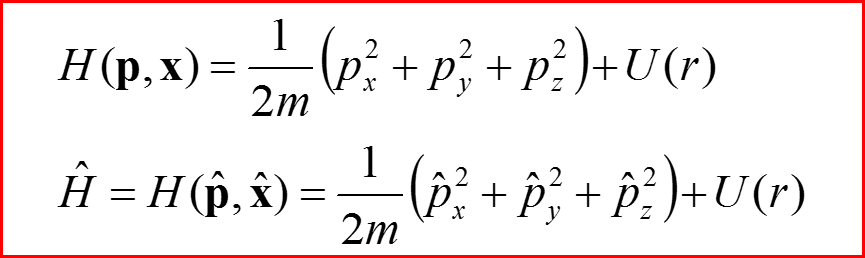
13
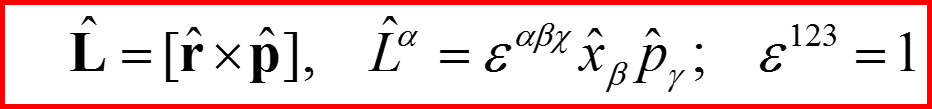
14
II. Уравнение Шредингера для центрального поля
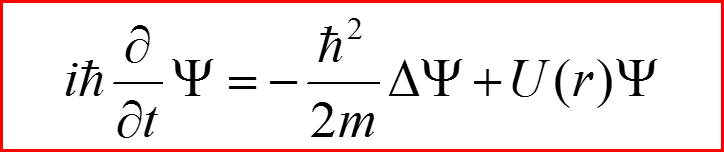
15
Стационарные состояния
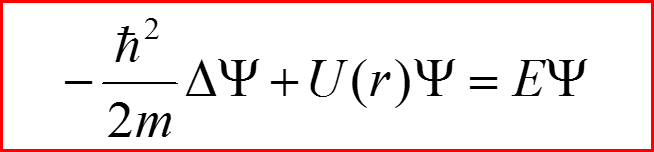
16
II. Закон сохранения момента импульса
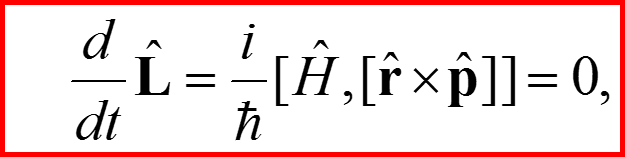
17
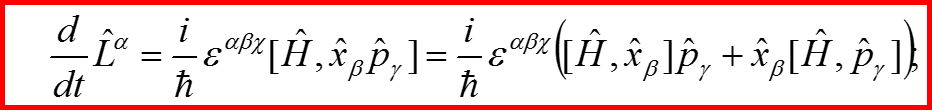
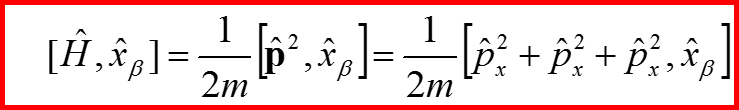
18
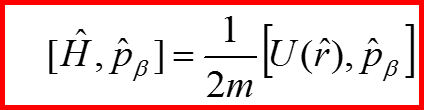
19
II. Закон сохранения момента импульса
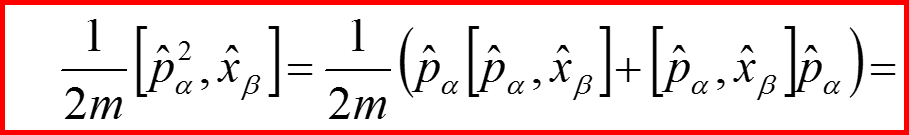
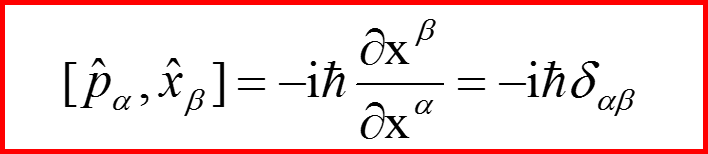
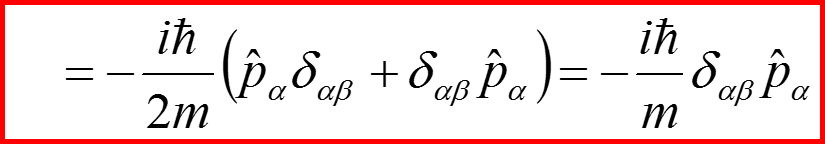
20
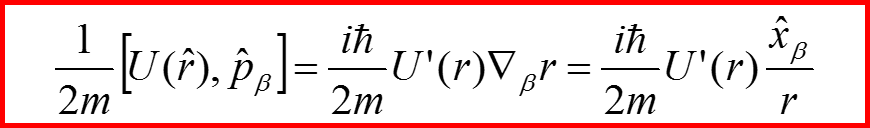
21
II. Закон сохранения момента импульса
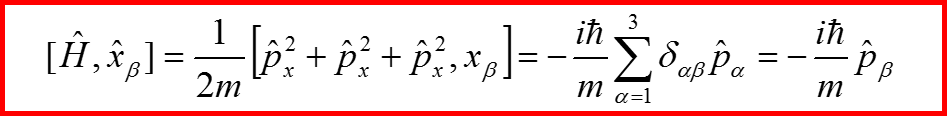
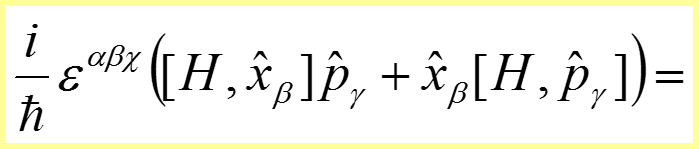
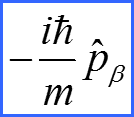
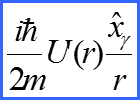
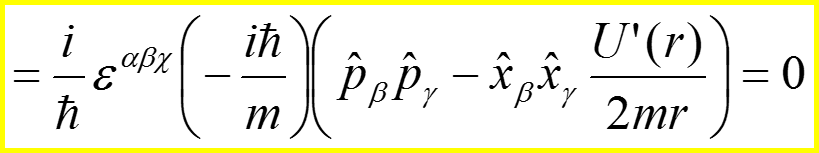
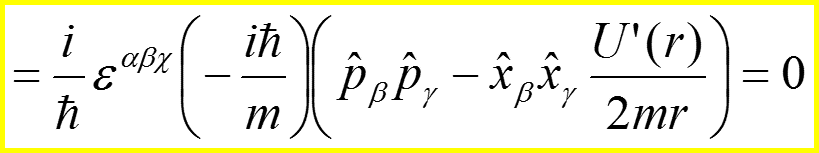
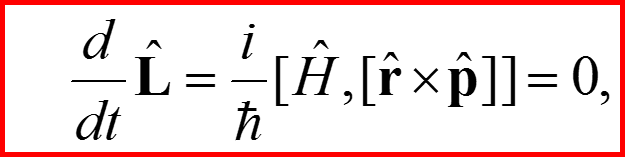
22
Уравнение Шредингера для радиального движения
Разделение переменных
![]()
III. Уравнение Шредингера в сферической системе координат
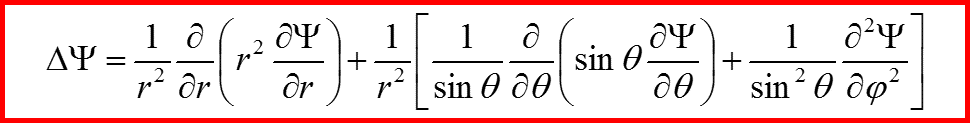
Стационарные состояния
![]()
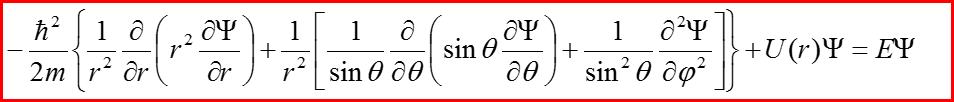
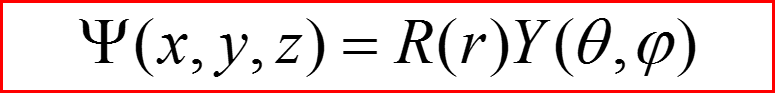
III. Разделение переменных в сферической системе координат
Разделение переменных в уравнении означает, что оператор Гамильтона обладает симметрией определенного типа – в данном случае - сферической
III. Разделение переменных в сферической системе координат
Радиальное движение
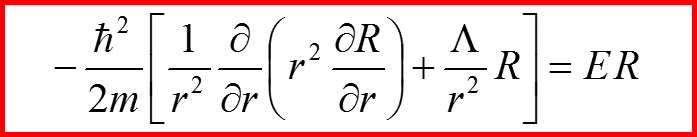
23
![]()
Угловое движение
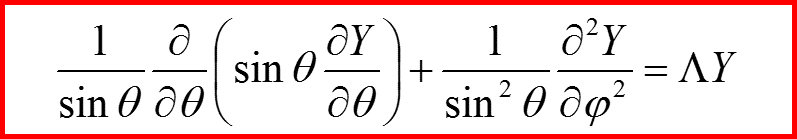
24
Угловое движение Оператор момента импульса
Как устроена волновая функция углового движения?
IV. Операторы проекции орбитального момента на оси координат
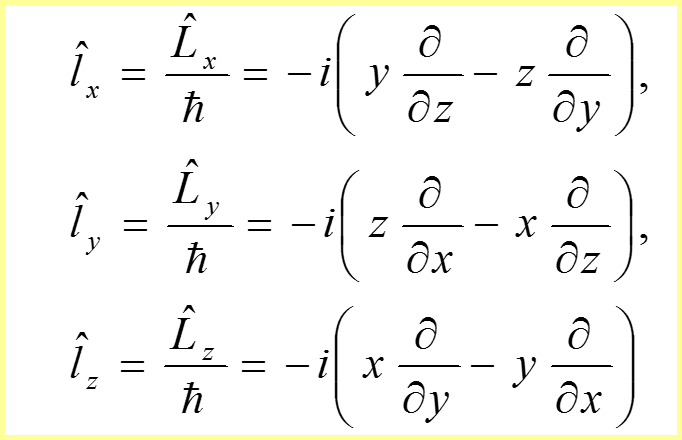
25
IV. Операторы проекции орбитального момента
Коммутационные соотношения:
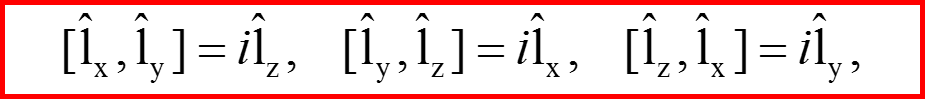
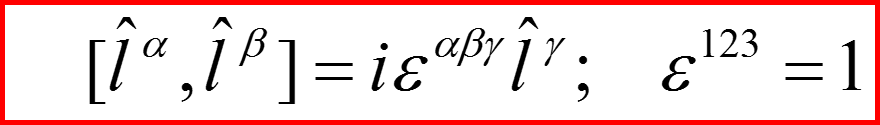
26
IV. Операторы проекции орбитального момента
Сферическая система координат:
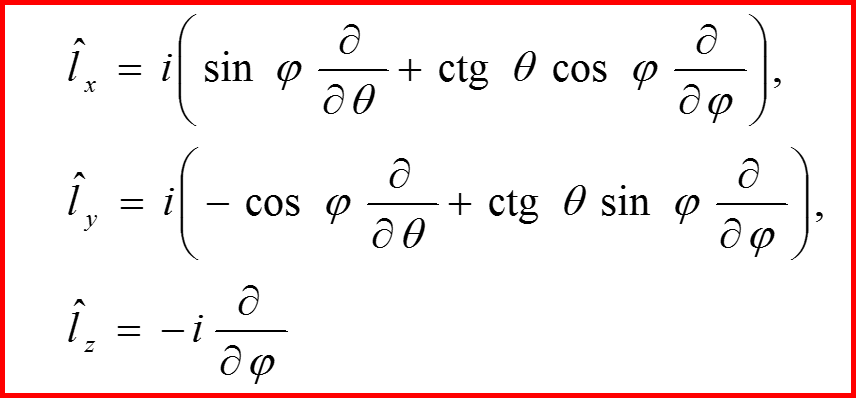
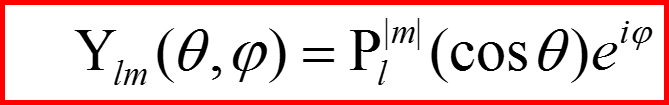
27
IV. Собственные функции оператора lz
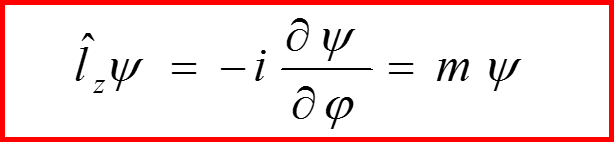
28
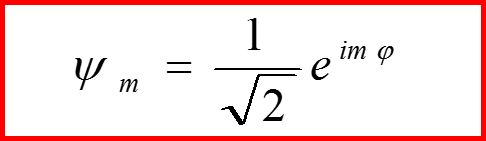
29

IV. Оператор квадрата орбитального момента
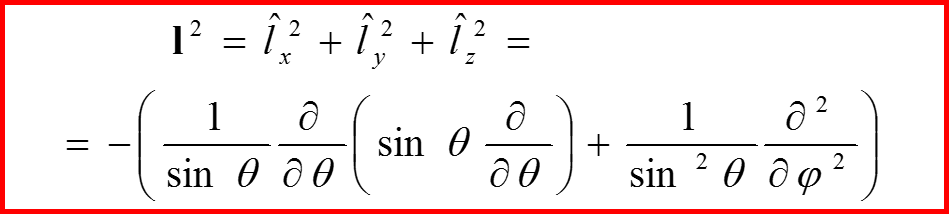
Коммутационные соотношения:
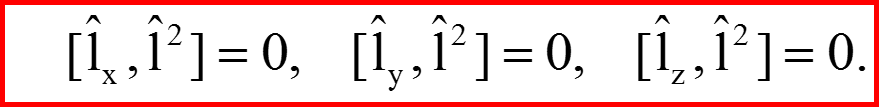
30
IV. Собственные функции квадрата орбитального момента
Что означает ситуация, когда оператор коммутирует со всеми операторами, которые между собой не коммутируют?
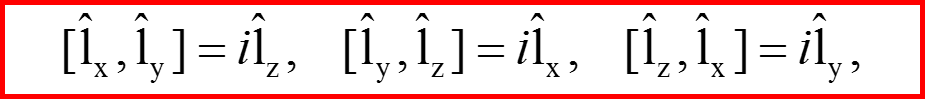
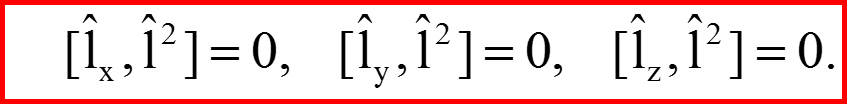
31
IV. Собственные функции квадрата орбитального момента
Пространство собственных функций квадрата орбитального момента представляет собой прямое произведение пространств собственных функций проекций орбитального момента на оси координат!!!
IV. Собственные функции квадрата орбитального момента
Собственными функциями квадрата орбитального момента являются cферические гармоники:
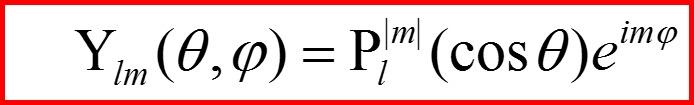
32
Присоединенные полиномы Лежандра

IV. Собственные функции квадрата орбитального момента
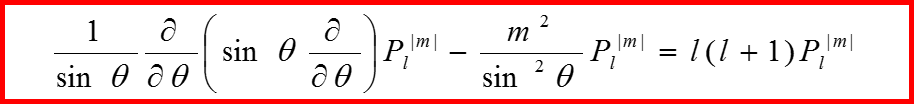
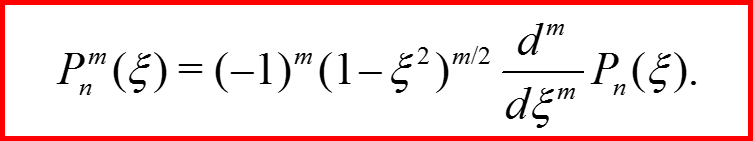
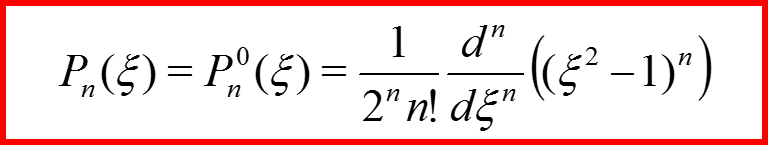
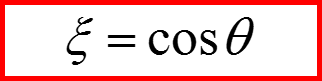
33
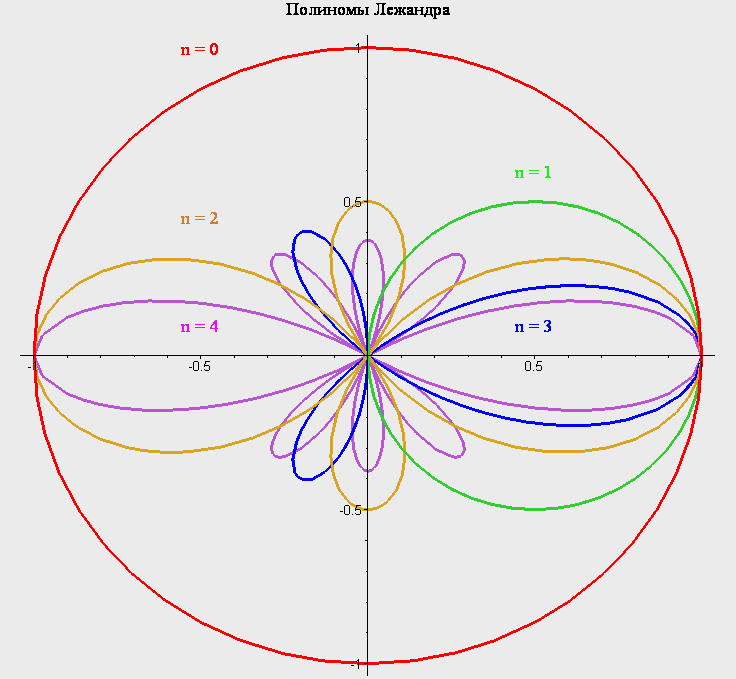
Полином Лежандра P0

Полином Лежандра P1
Полином Лежандра P2
Полином Лежандра P3
Полином Лежандра P4
IV. Операторы l+ и l-
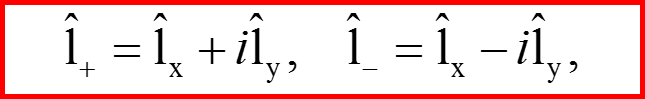
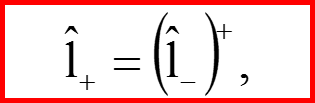
35
Коммутационные соотношения:
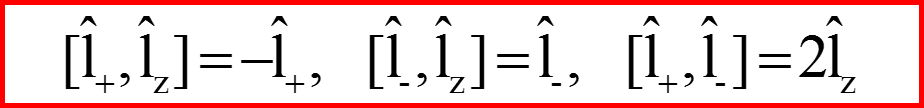
36
IV. Операторы l+ и l-
Представление оператора l 2
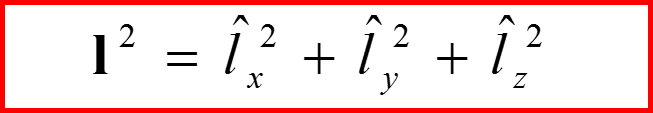
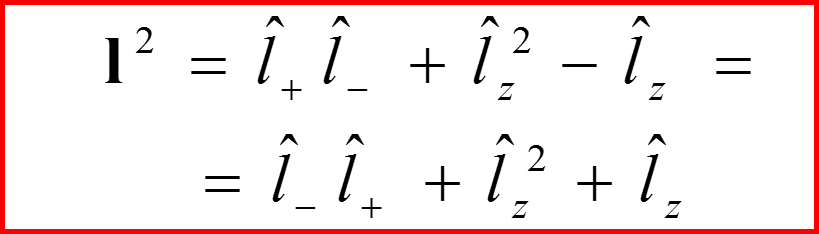
37
IV. Операторы l+ и l-
Лестничные операторы
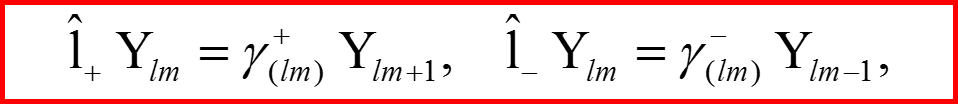
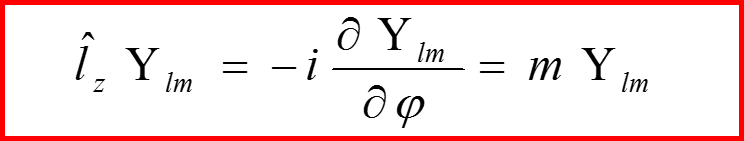
38
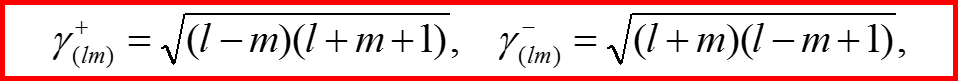
IV. Операторы l+ и l-
Вычисление коэффициентов сдвига
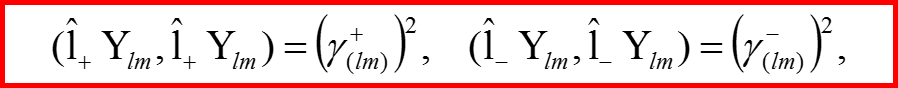
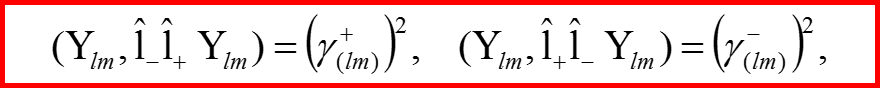
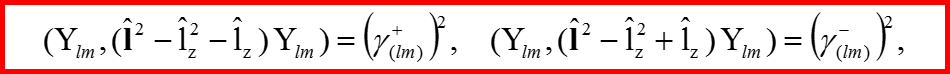
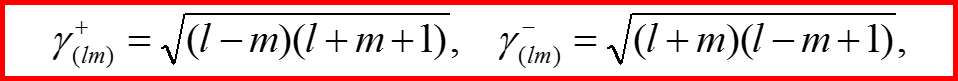
39
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.