




































Квантовая теория
![]()
Семестр I
Лекция X
Тема: Движение в центральном поле. Лестничные операторы в центральном поле
Чем отличаются состояния в трехмерных потенциальных ямах от состояний в одномерных?
Операторы l+ и l- - лестничные операторы по магнитному квантовому числу
![]()
Как найти собственные числа оператора l2?
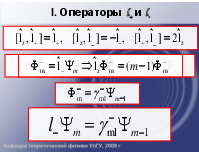
I. Операторы l+ и l-
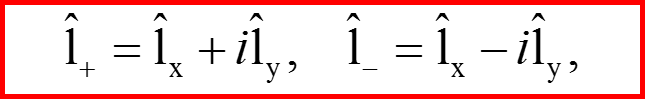
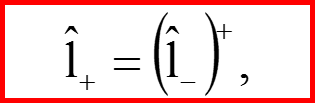
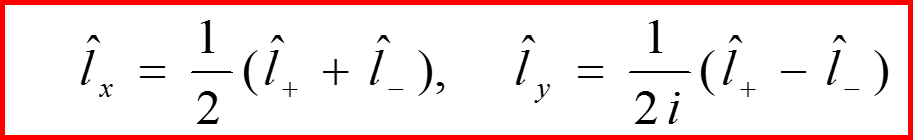
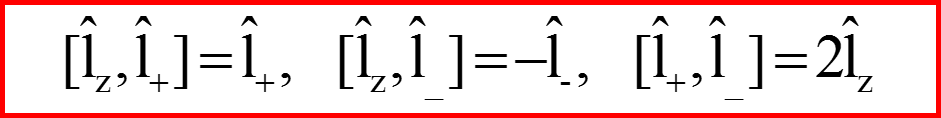
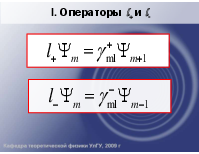
I. Операторы l+ и l-
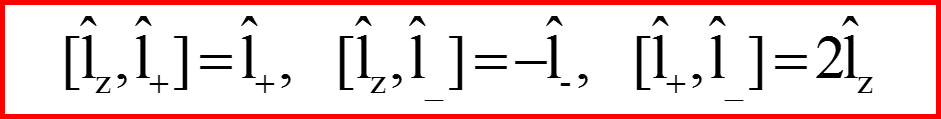
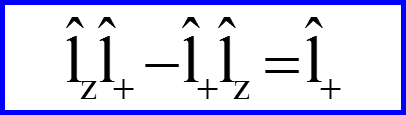

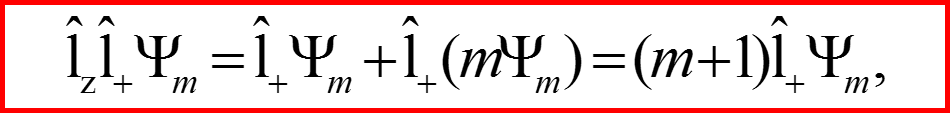
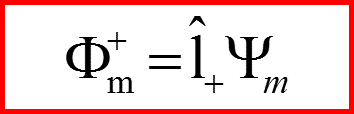
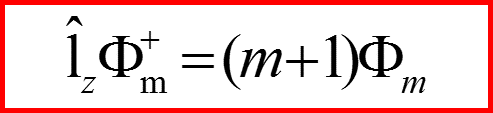
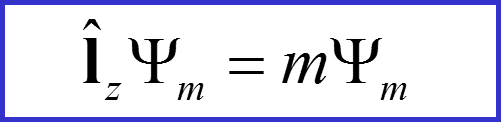
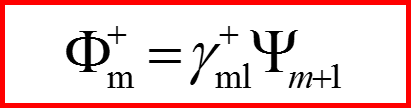
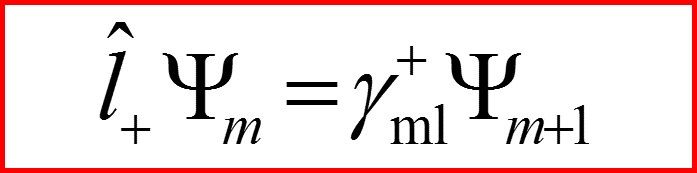
I. Операторы l+ и l-
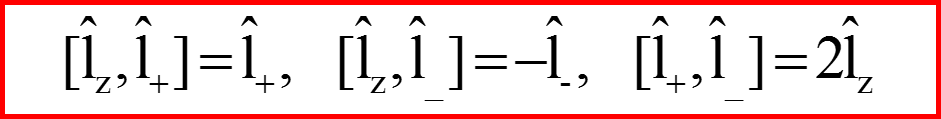

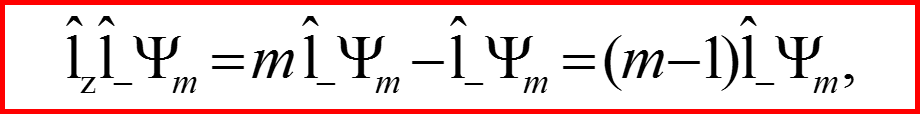
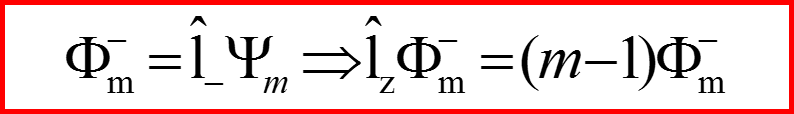
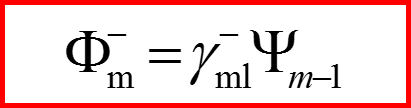
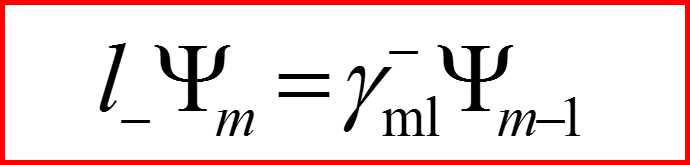
I. Операторы l+ и l-
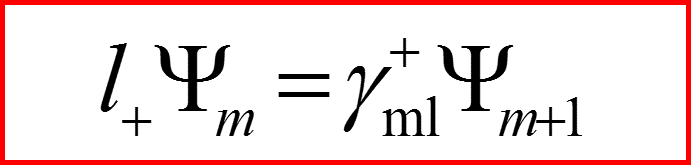
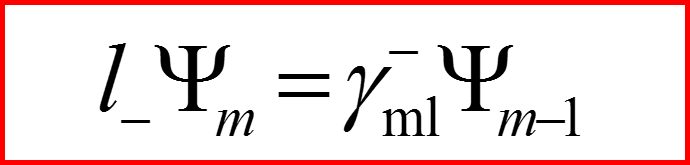
I. Операторы l+ и l-
Лестничные операторы
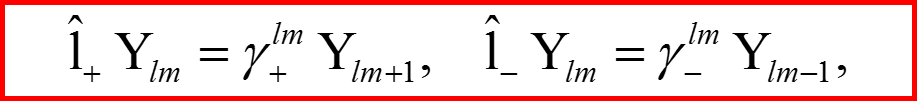
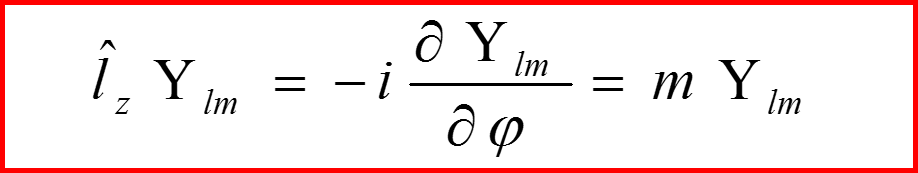
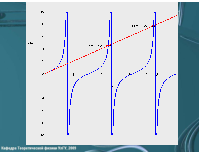
II. Оператор l 2
Представление оператора l 2
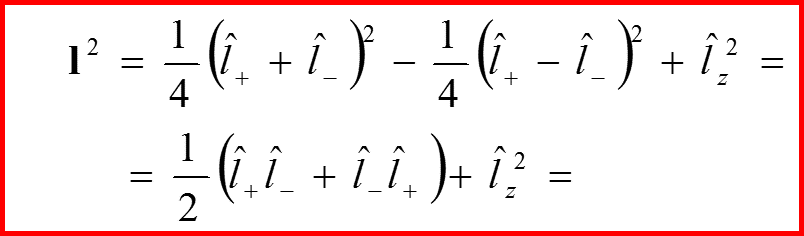

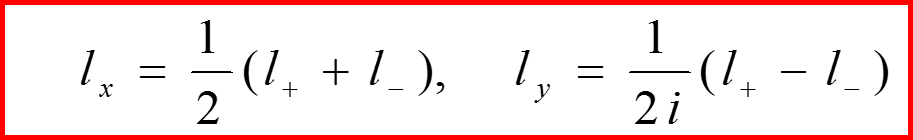
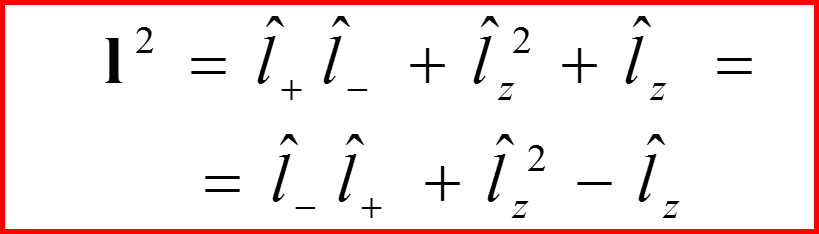
II. Оператор l 2
Собственные значения оператора l 2
Обозначим через Λ собственное число оператора l 2, соответствующее фиксированному значению квадрата орбитального момента. Соответствующее собственное значение (магнитное квантовое число) проекции орбитального момента lz обозначим через l =mmax. Тогда:
II. Собственные числа оператора l 2
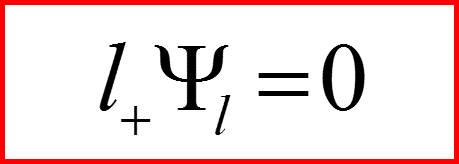
Число l называется орбитальным квантовым числом
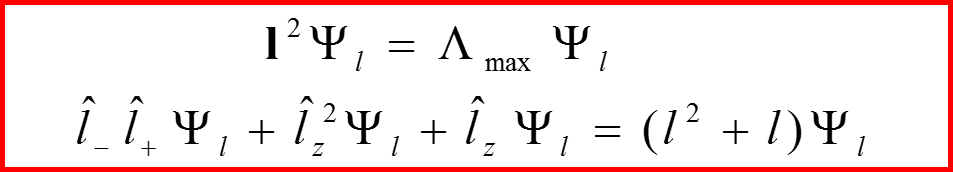
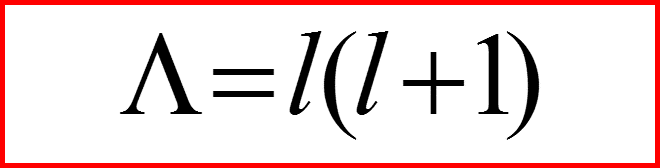
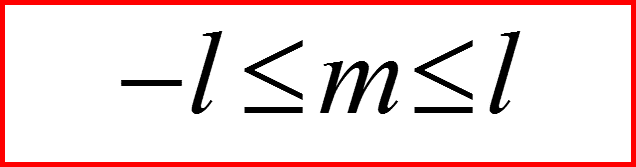
Движение в центральном поле
![]()
Как найти собственные числа оператора l2?
III. Уравнение Шредингера для радиального движения
Классические законы сохранения
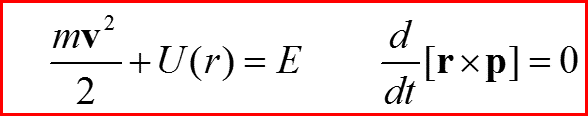
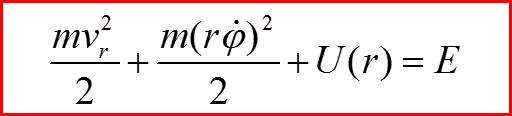
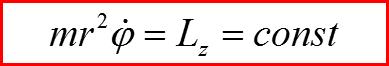
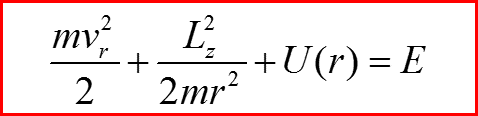
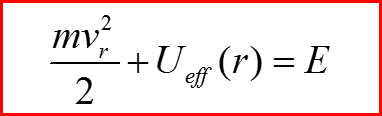
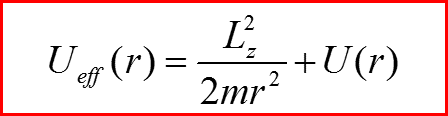
III. Уравнение Шредингера для радиального движения
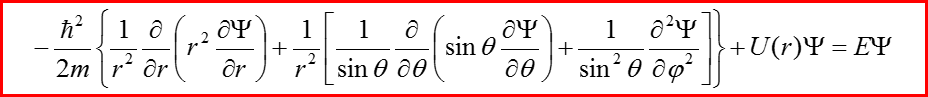
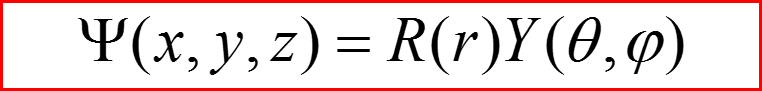
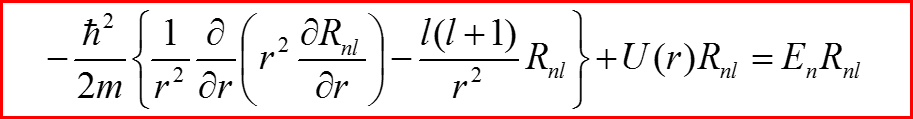
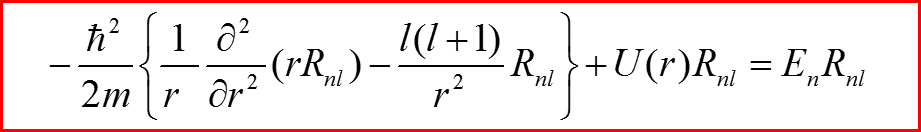
n –главное квантовое число
III. Уравнение Шредингера для радиального движения
Полная совокупность квантовых чисел для центрального поля (n,l,m): n – главное квантовое число l – орбитальное квантовое число m – магнитное квантовое число
III. Уравнение Шредингера для радиального движения
Введем обозначение:
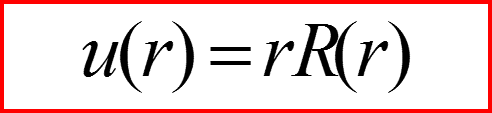
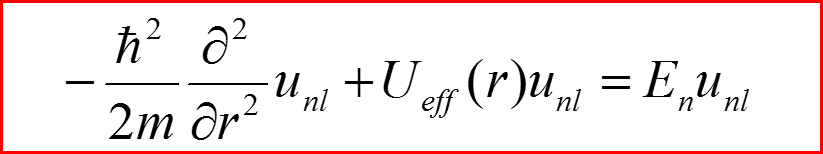

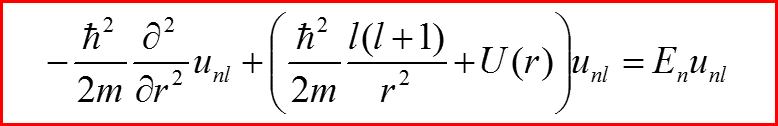
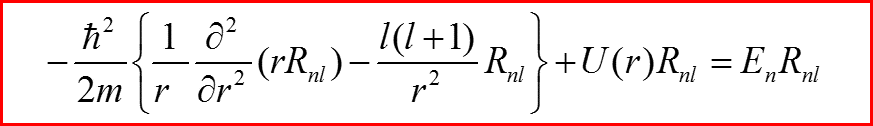
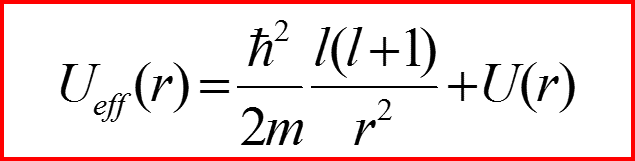
III. Уравнение Шредингера для радиального движения
Граничные условия финитного движения:
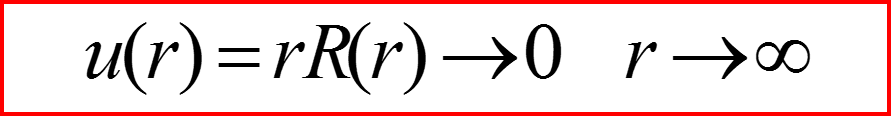
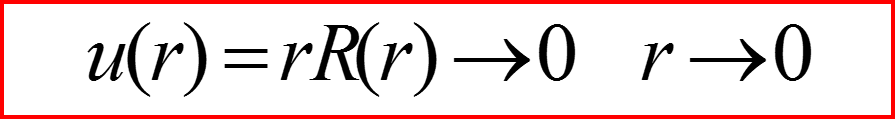
III. Уравнение Шредингера для радиального движения
Граничные условия инфинитного движения:

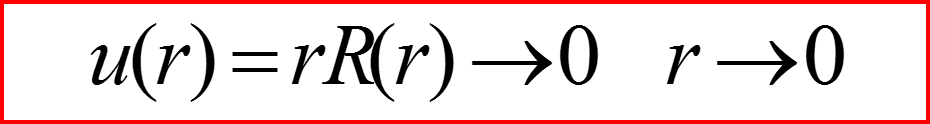
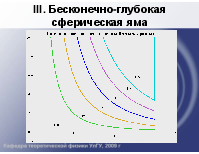
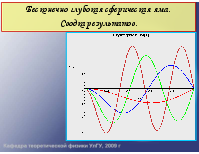
Бесконечно глубокая сферическая яма
Метод лестничных операторов
![]()
III. Бесконечно-глубокая сферическая яма
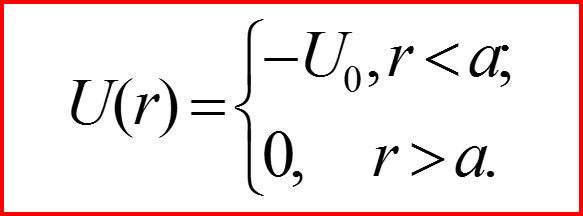
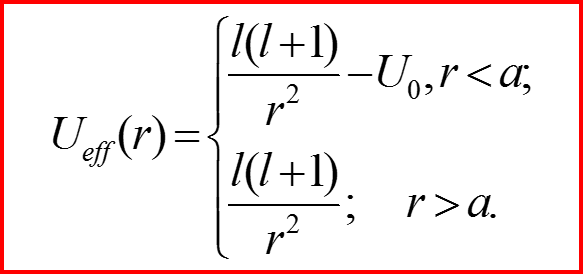
III. Бесконечно-глубокая сферическая яма
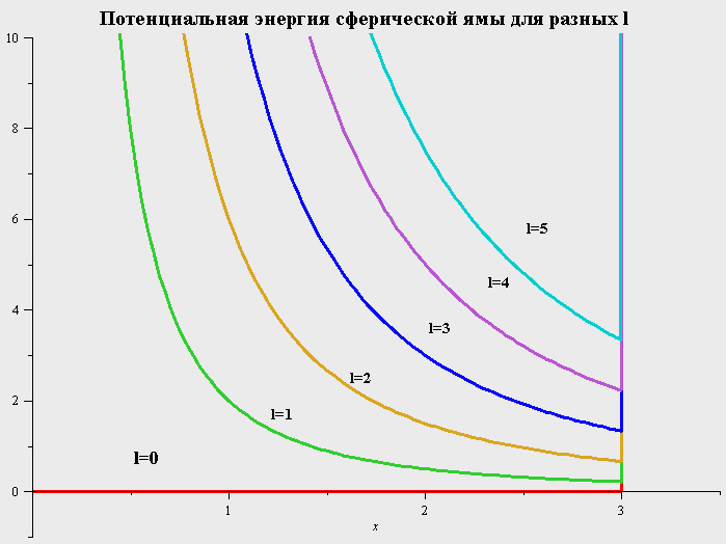
III. Бесконечно-глубокая сферическая яма
Оператор Гамильтона
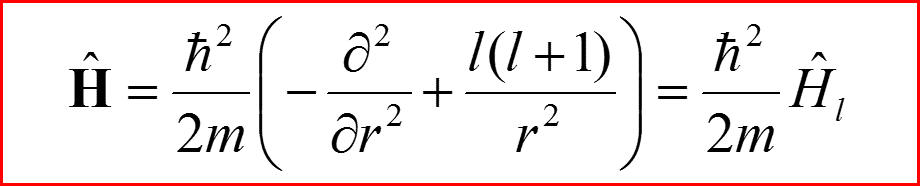
III. Бесконечно-глубокая сферическая яма
Уравнение Шредингера
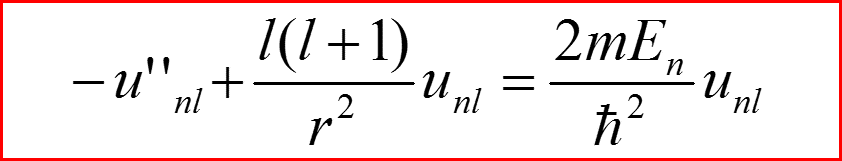
Граничные условия
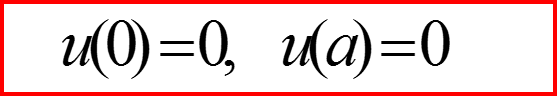
III. Бесконечно-глубокая сферическая яма
l=0
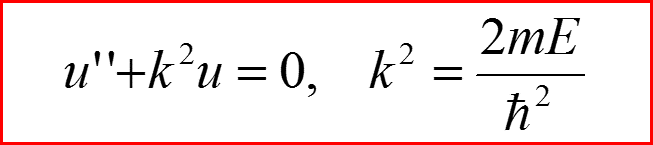
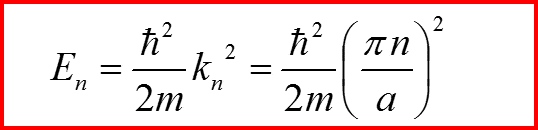
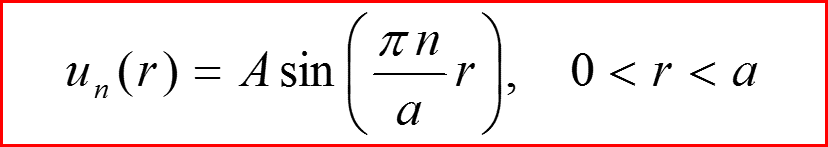
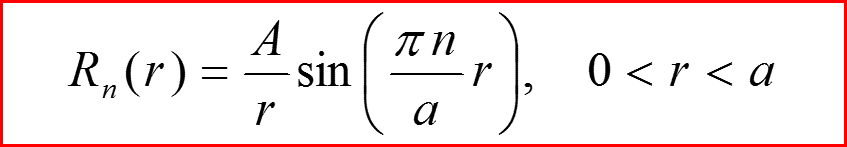
III. Бесконечно-глубокая сферическая яма
l=0 Нормировка
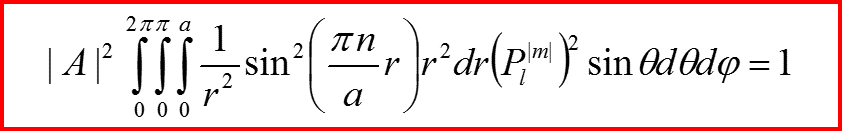
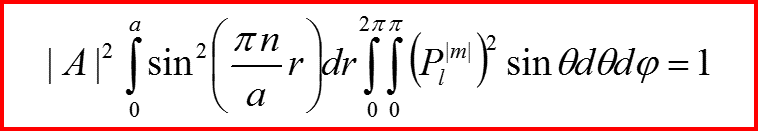
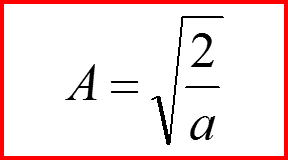
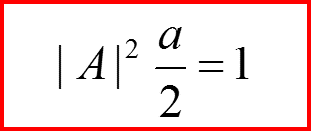
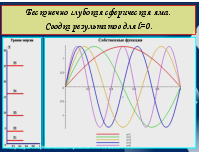
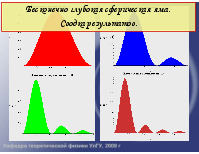
Бесконечно глубокая сферическая яма. Сводка результатов для l=0.
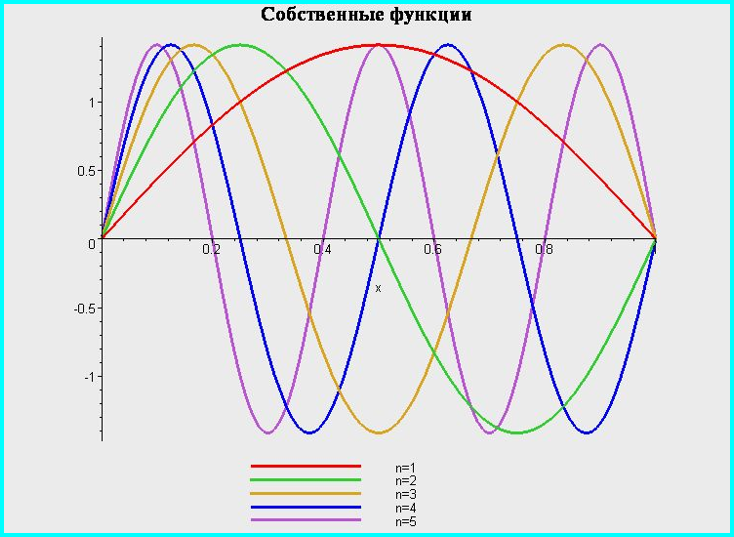
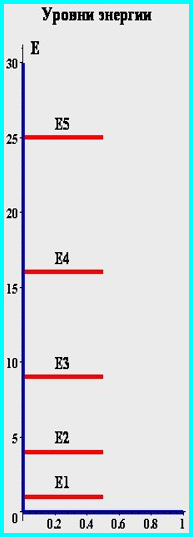
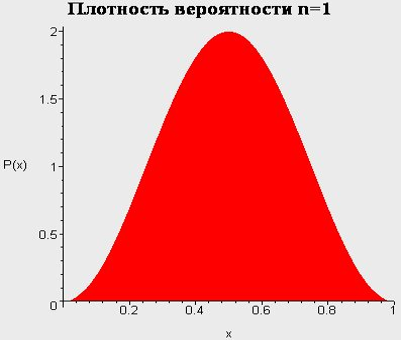
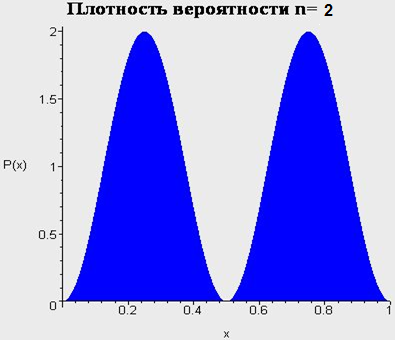
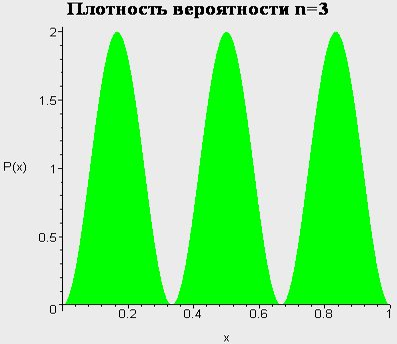
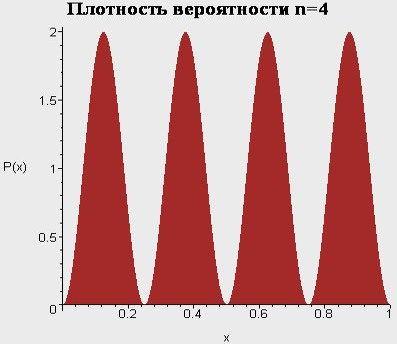
IV. Бесконечно-глубокая сферическая яма, l>0
l>0
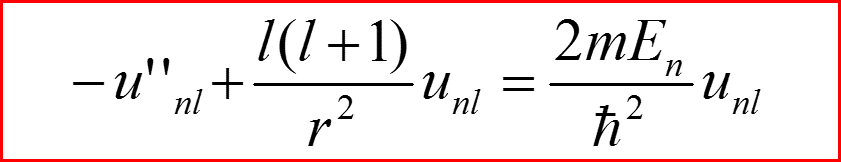
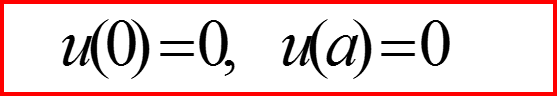
IV. Бесконечно-глубокая сферическая яма, l>0
Лестничные операторы
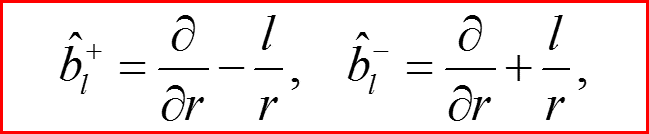
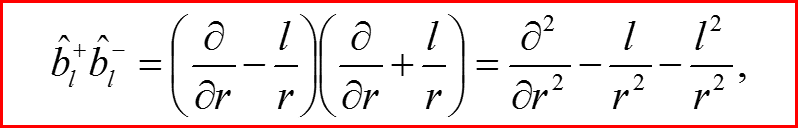
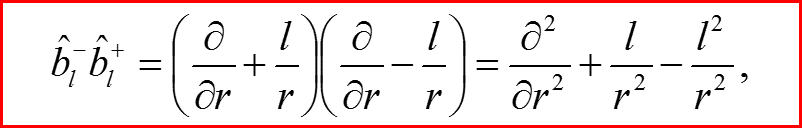
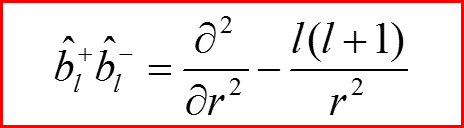
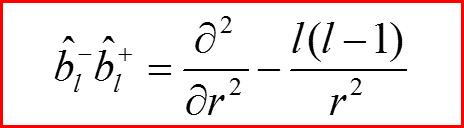
IV. Бесконечно-глубокая сферическая яма, l>0
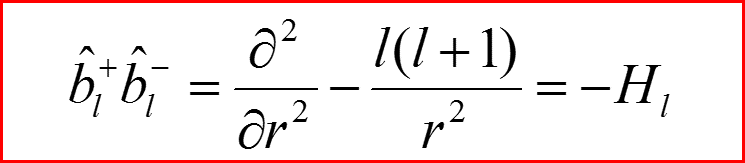
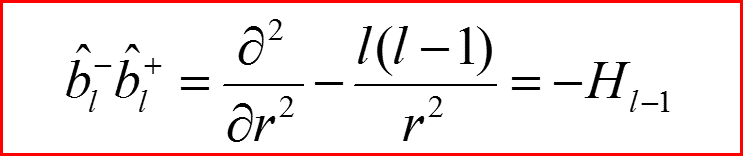
IV. Бесконечно-глубокая сферическая яма, l>0
Уравнения Шредингера
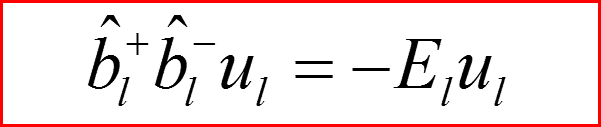
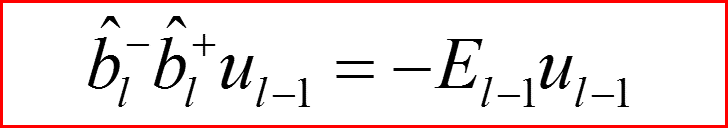
IV. Бесконечно-глубокая сферическая яма, l>0
Операции перехода по орбитальному числу.
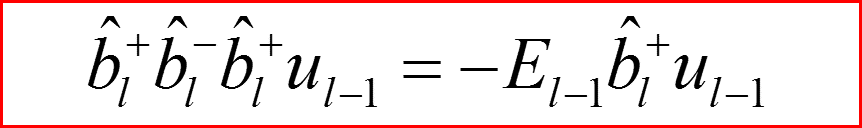
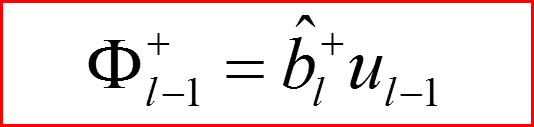
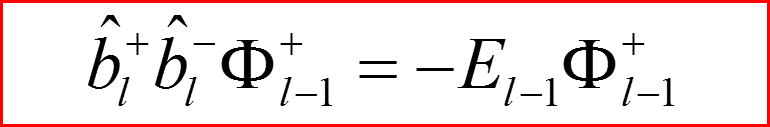
IV. Бесконечно-глубокая сферическая яма, l>0
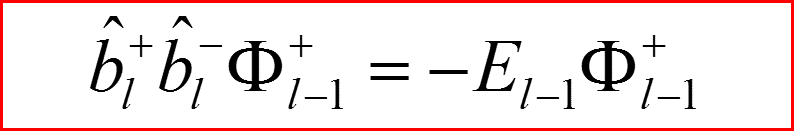

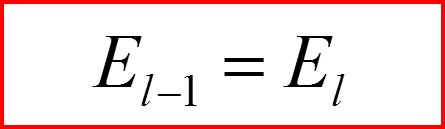
Повышающий оператор по l.
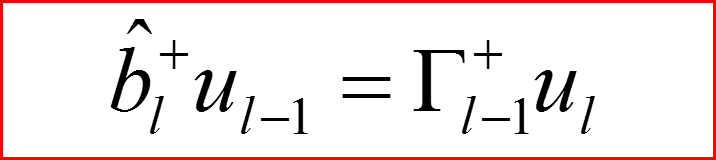
IV. Бесконечно-глубокая сферическая яма, l>0
Операции перехода по орбитальному числу.
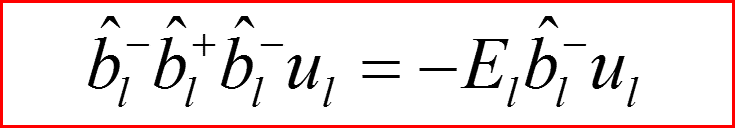
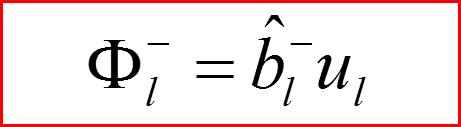
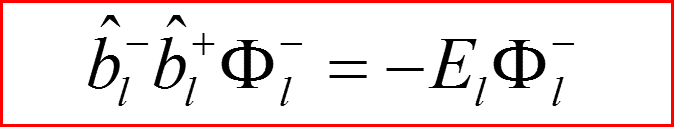
IV. Бесконечно-глубокая сферическая яма, l>0
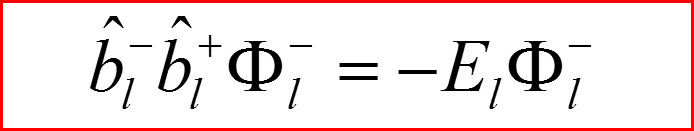
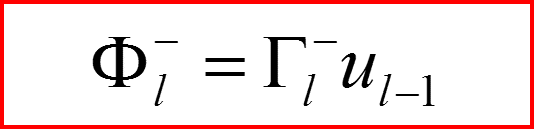
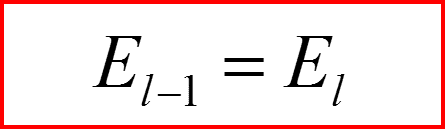
Понижающий оператор по l.
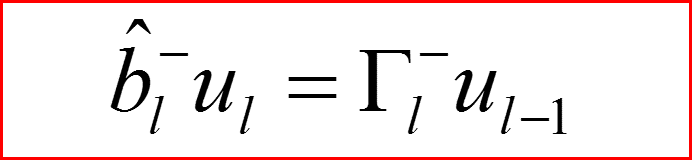
IV. Бесконечно-глубокая сферическая яма, l>0
l=1
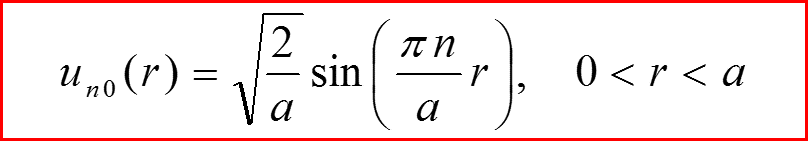
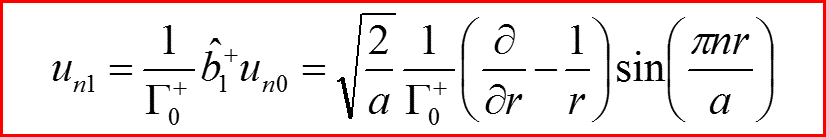
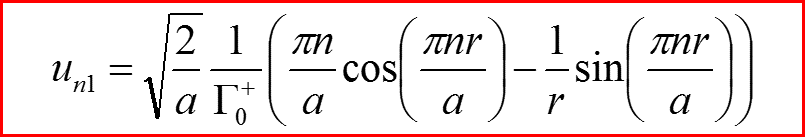
IV. Бесконечно-глубокая сферическая яма, l>0
l=1, Проверка граничных условий
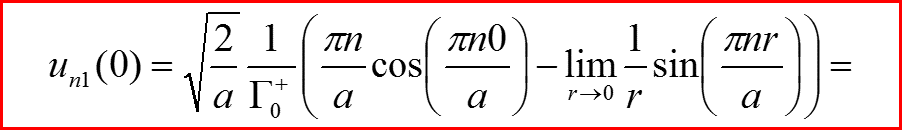
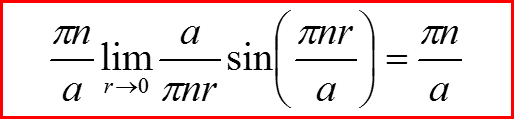
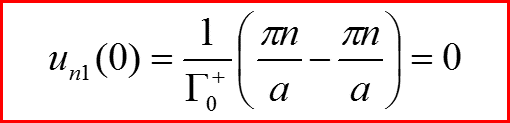
IV. Бесконечно-глубокая сферическая яма, l>0
l=1, Проверка граничных условий
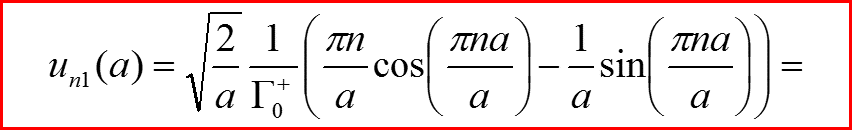
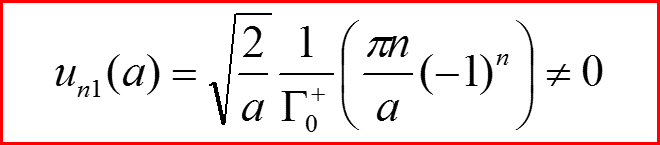
В чем причина!!???
IV. Бесконечно-глубокая сферическая яма, l>0
l=1. Исправление функций
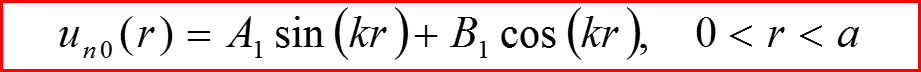
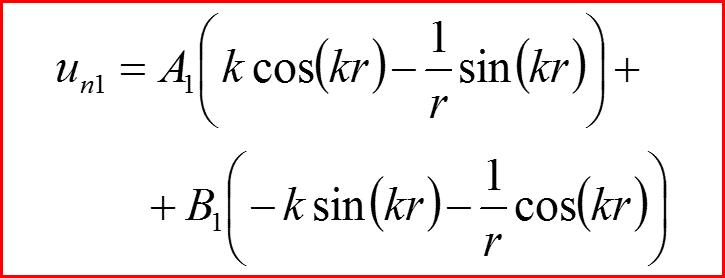
IV. Бесконечно-глубокая сферическая яма, l>0
l=1, Проверка граничных условий
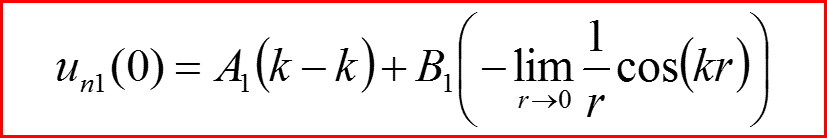
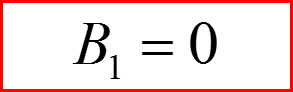
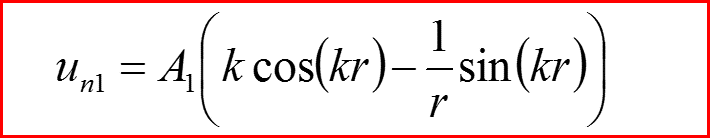
IV. Бесконечно-глубокая сферическая яма, l>0
l=1, Проверка граничных условий
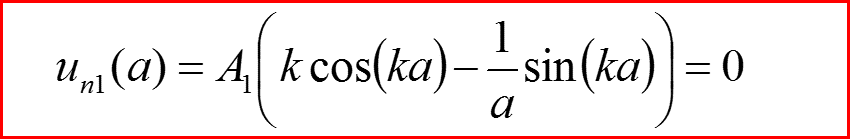
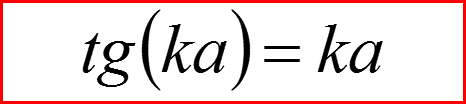
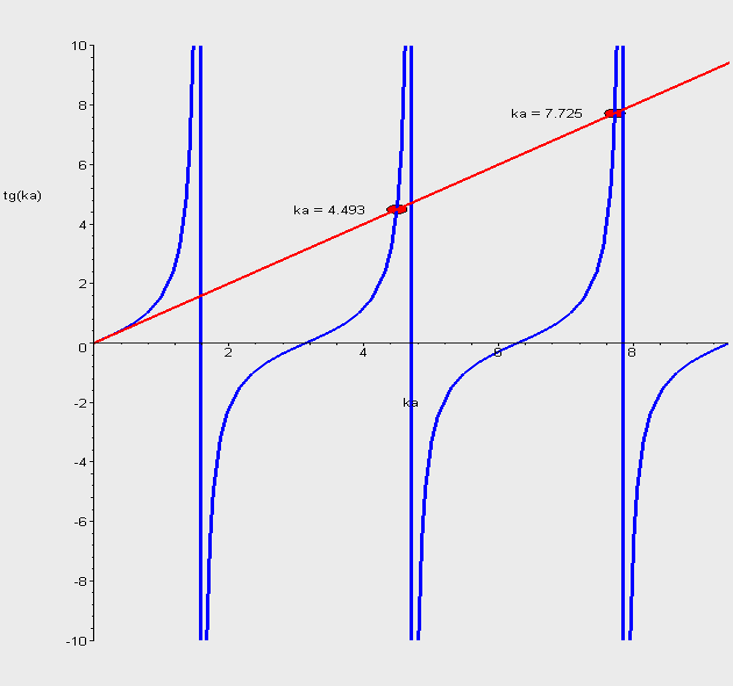
IV. Бесконечно-глубокая сферическая яма, l>0
l=1: Сводка результатов
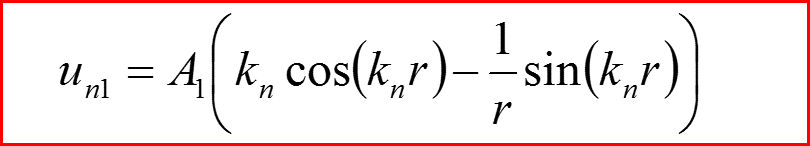
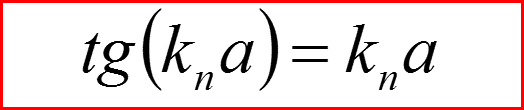
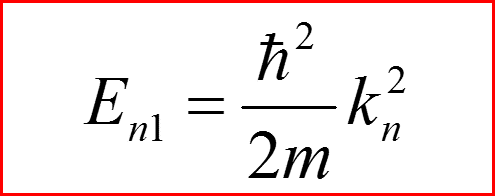
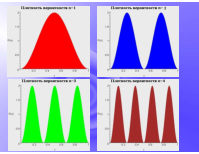
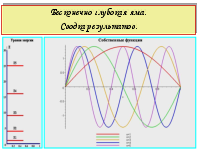
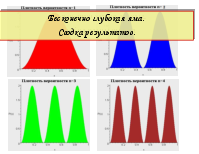
Бесконечно глубокая сферическая яма. Сводка результатов.
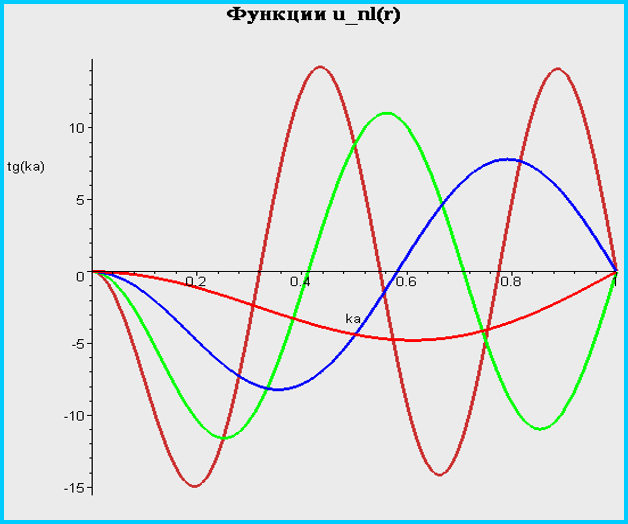
Бесконечно глубокая яма. Сводка результатов.
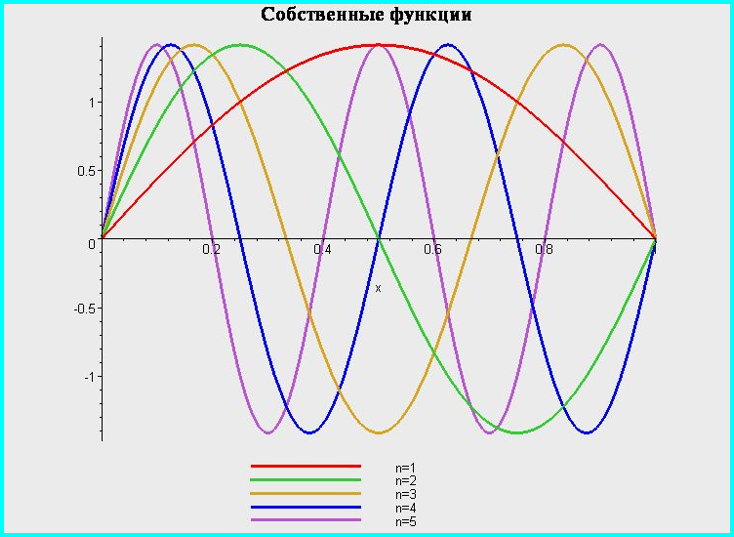
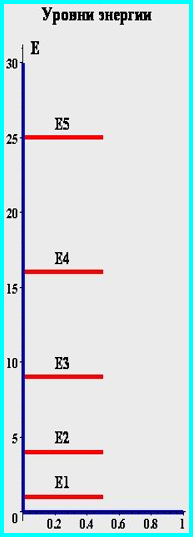
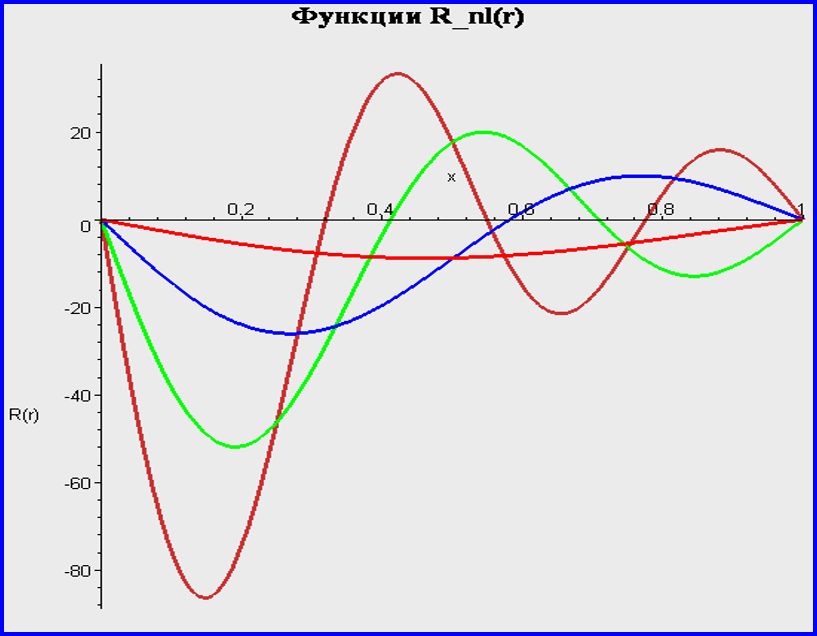
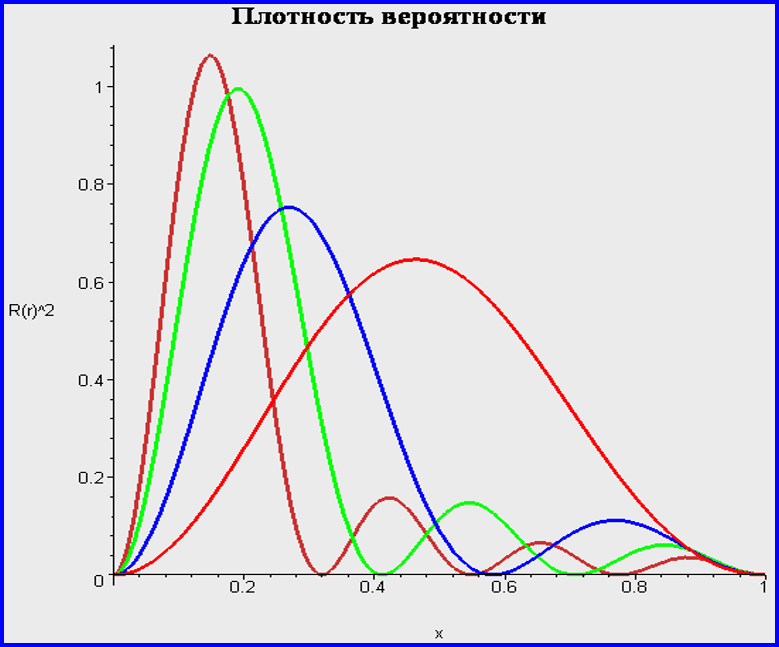
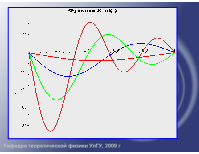
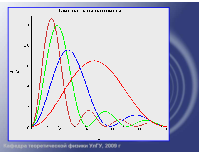
Бесконечно глубокая сферическая яма. Сводка результатов.
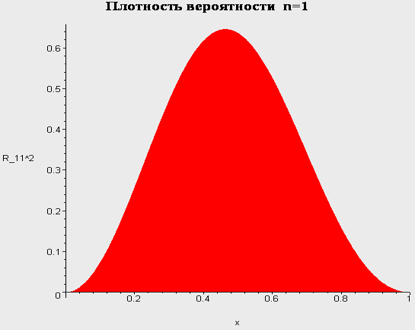
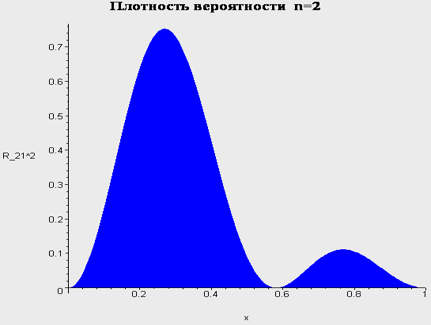
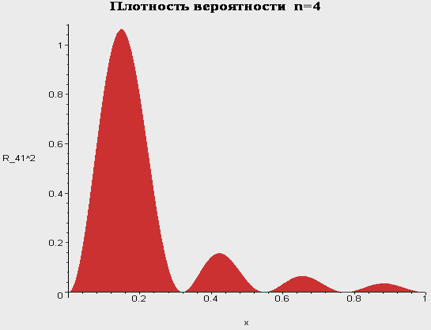
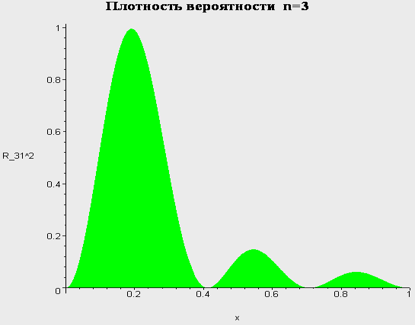
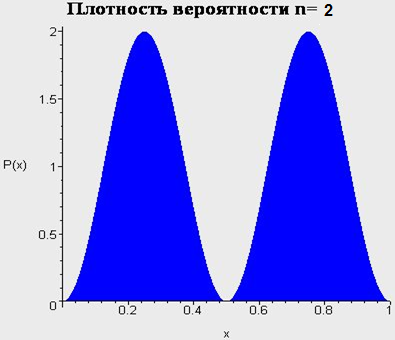
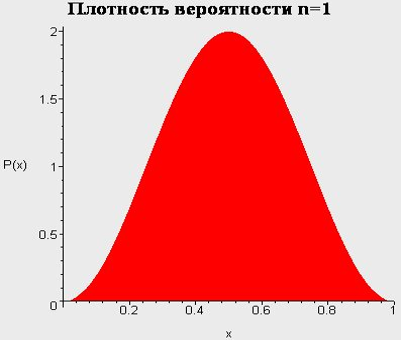
Бесконечно глубокая яма. Сводка результатов.
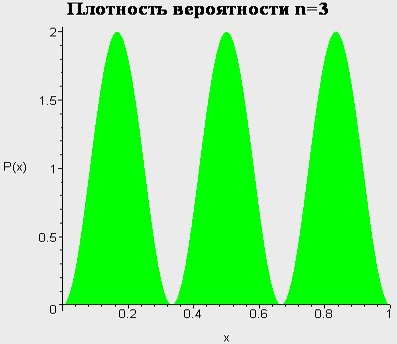
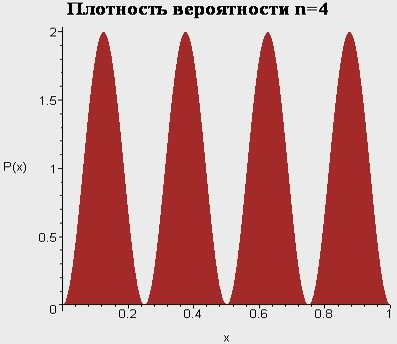
Атом водорода
Метод лестничных оператров
![]()
Следующая лекция
![]()
Атом водорода
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.