Квантовая теория
![]()
Семестр I
Лекция XI
Атом водорода
Метод лестничных операторов в теории атома водорода
Уравнение Шредингера для атома водорода
![]()
Почему задача движения в кулоновском поле полностью интегрируется?
I. Оператор Гамильтона для атома водорода и законы сохранения
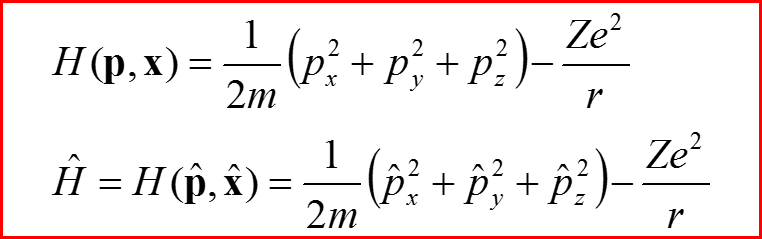
Энергия
Момент
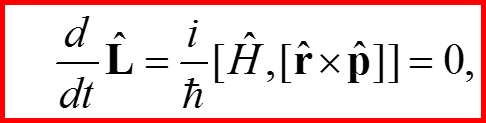
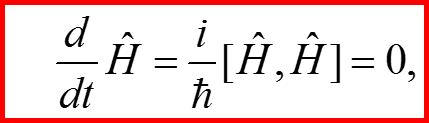
I. Определение полной интегрируемости
В классической механике система называется полностью интегрируемой, если закон движения можно представить в квадратурах!
Примеры: гармонический осциллятор, кулоновский потенциал
I. Условие полной интегрируемости
Теорема Лиувилля: Для полной интегрируемости система должна обладать набором законов сохранения, число которых должно быть равно числу степеней свободы системы!
I. Дополнительный закон сохранения (Лапласа) для атома водорода
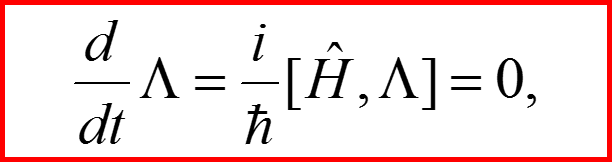
1
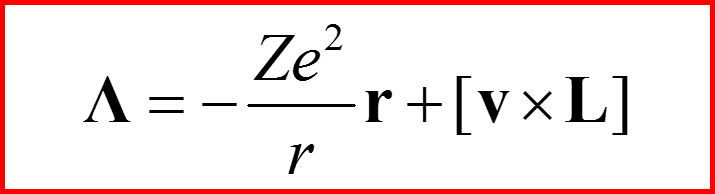
2
II. Уравнение Шредингера для радиального движения
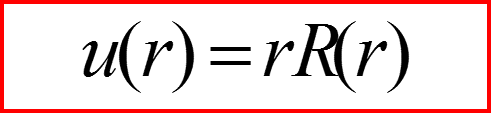
3
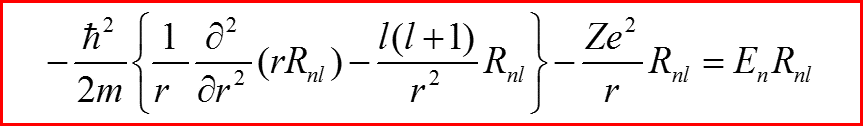
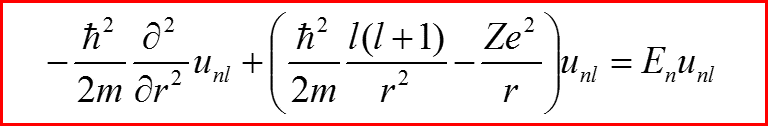
4
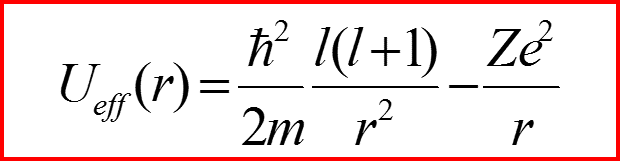
5
II. Уравнение Шредингера для радиального движения
Граничные условия финитного движения:
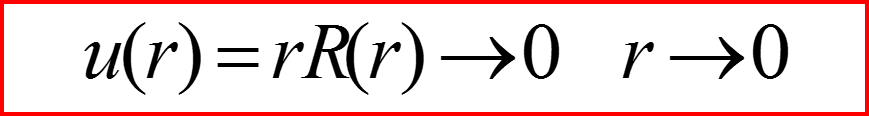
6
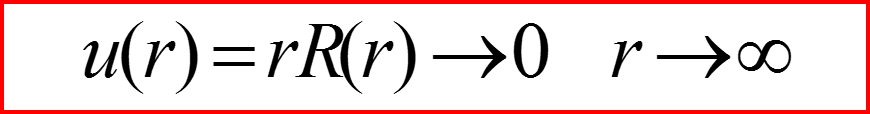
7
II. Приведенное уравнение Шредингера
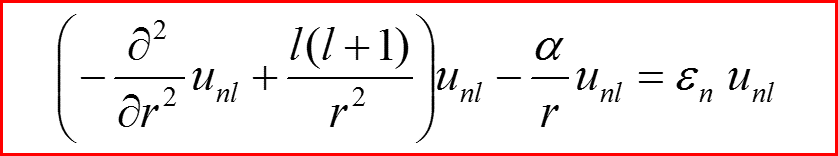
8
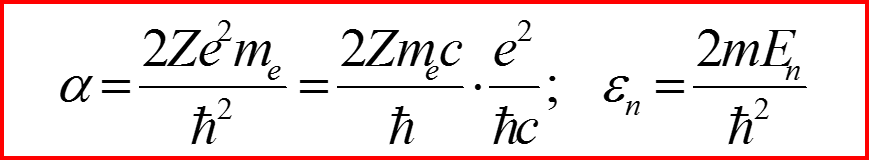
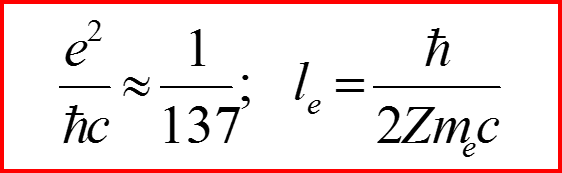
II. Эффективный потенциал
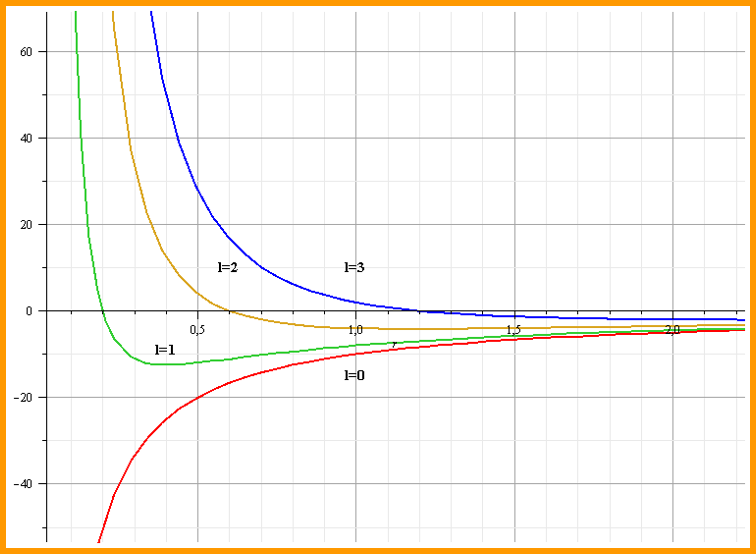
Радиальное уравнение для атома водорода
Метод лестничных операторов
![]()
III. Бесконечно-глубокая сферическая яма
Оператор Гамильтона
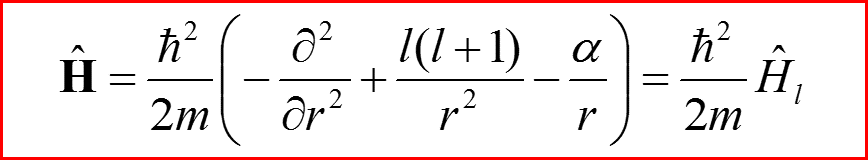
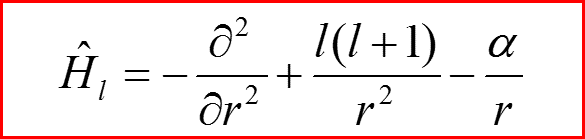
9
III. Атом водорода, l>0
Лестничные операторы с.б.г.я
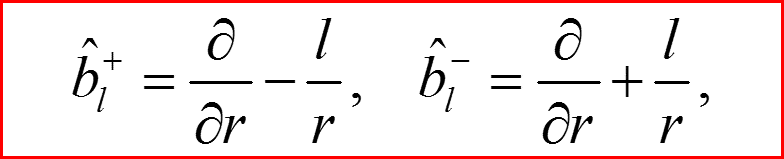
10
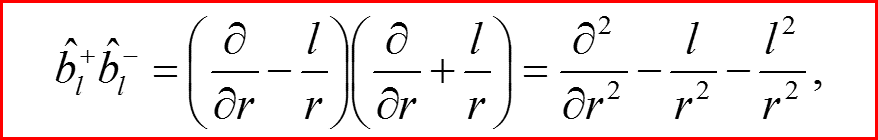
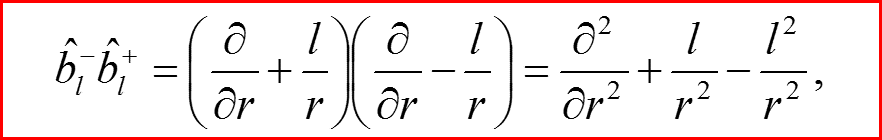
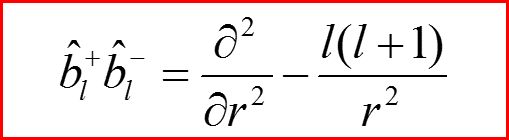
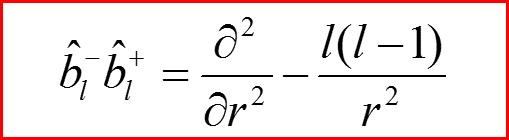
11
III. Атом водорода, l>0
Лестничные операторы атома водорода
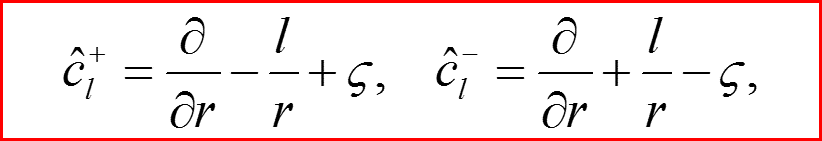
12
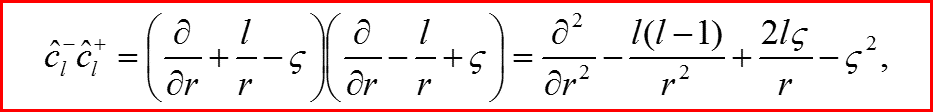
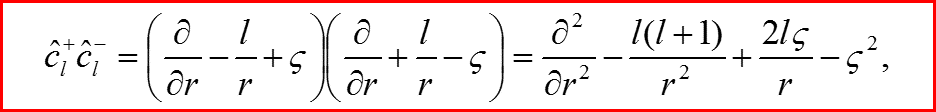
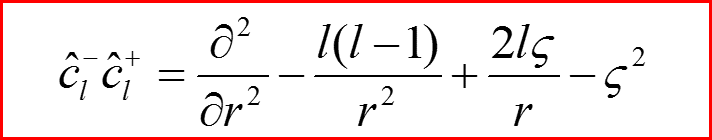
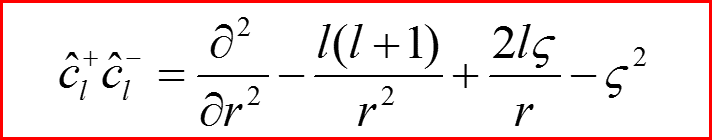
13
III. Атом водорода, l>0
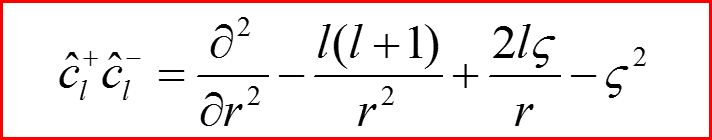
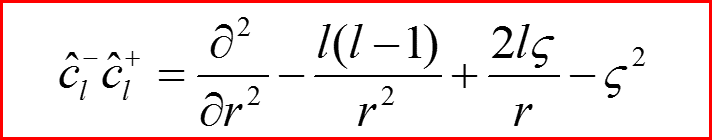
14
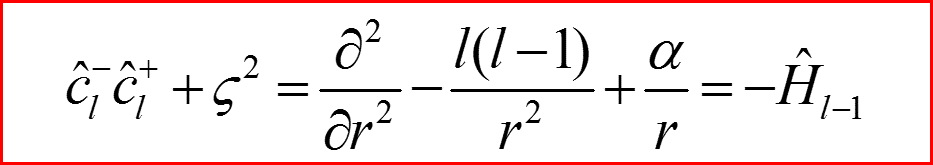
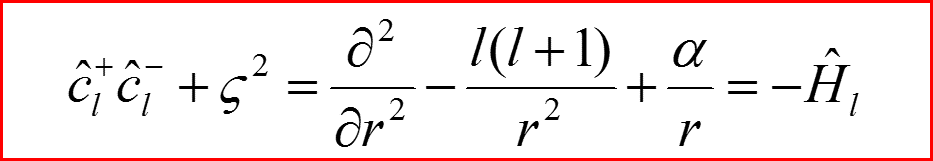
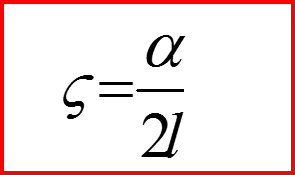
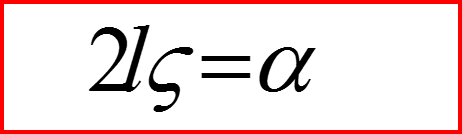
15
16
III. Атом водорода, l>0
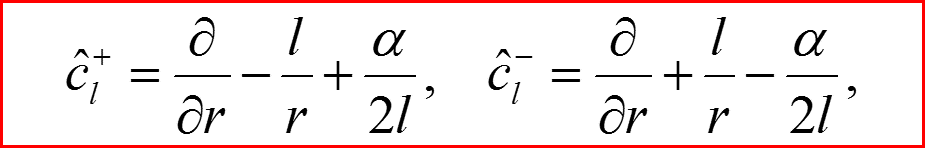
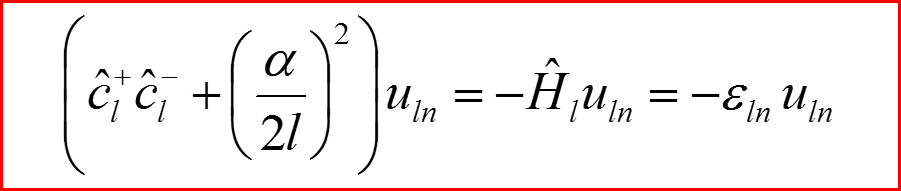
17
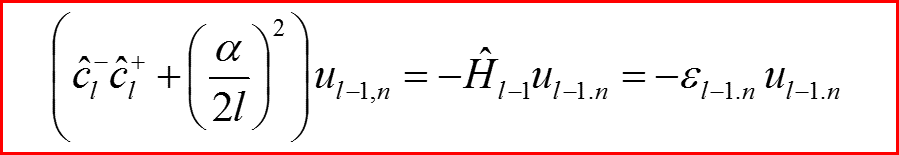
18
III. Атом водорода, l>0
Уравнение Шредингера
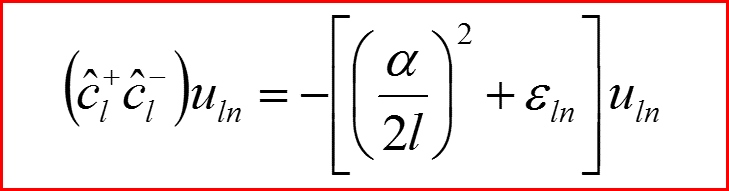
18
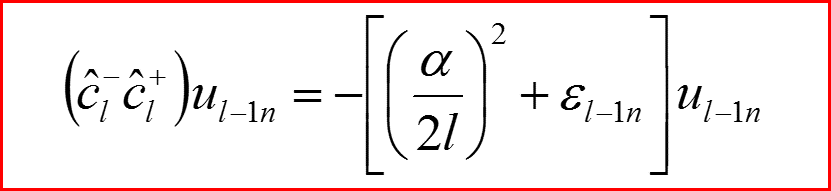
19
III. Атом водорода, l>0
Уравнения Шредингера
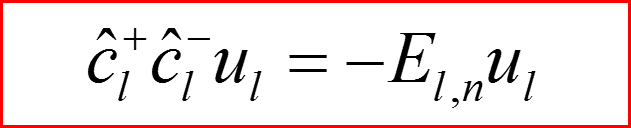
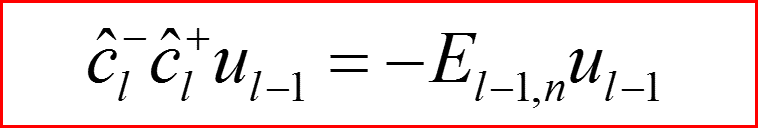
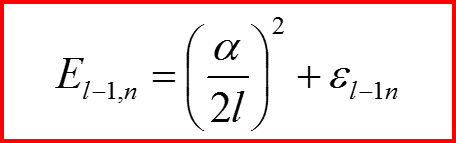
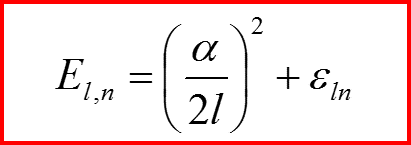
III. Атом водорода, l>0
Операции перехода по орбитальному числу.
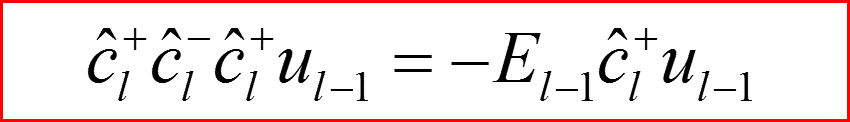
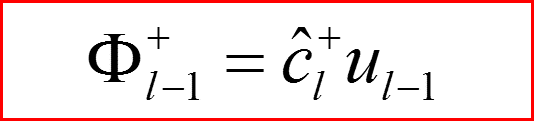
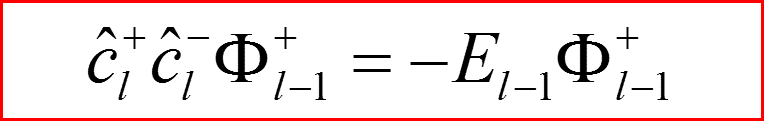
III. Атом водорода, l>0
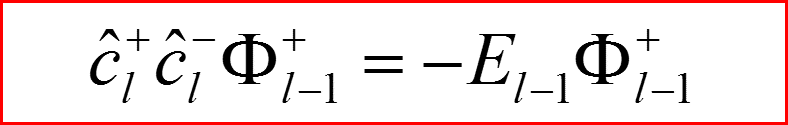
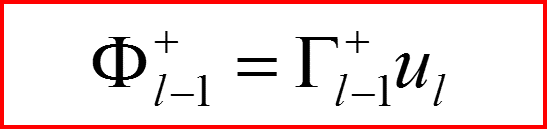
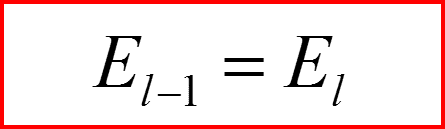
Повышающий оператор по l.
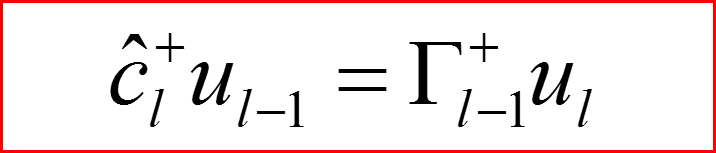
III. Атом водорода, l>0
Операции перехода по орбитальному числу.
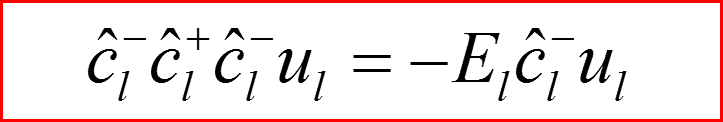
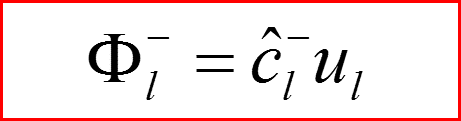
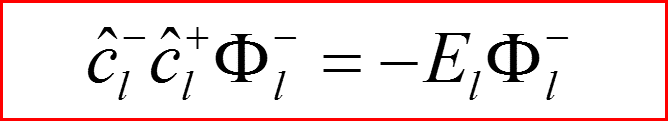
III. Атом водорода, l>0
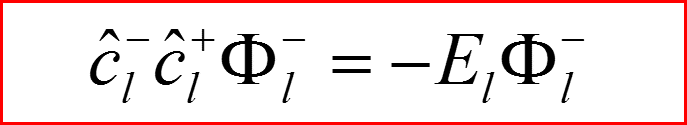
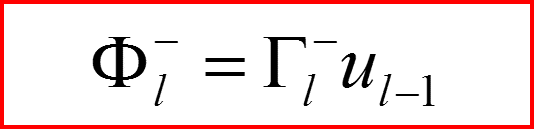
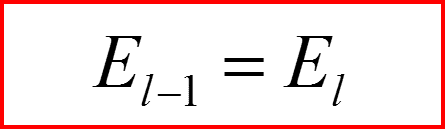
Понижающий оператор по l.
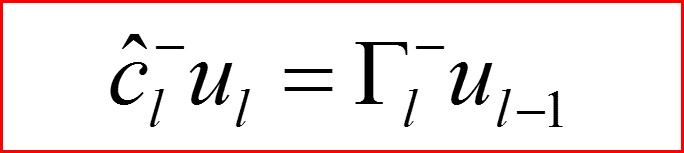
Собственные функции атома водорода
Метод лестничных операторов
![]()
IV. Собственные функции
Пусть E – некоторый уровень энергии. Обозначим через n максимальное орбитальное квантовое число, соответствующее этому фиксированному значению энергии E. Тогда:
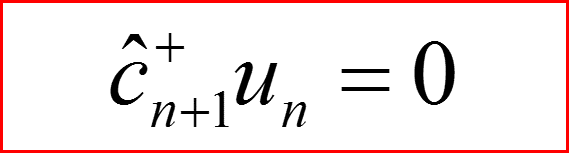
IV. Собственные функции
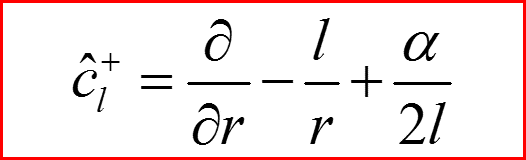
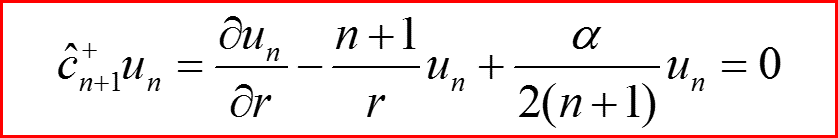
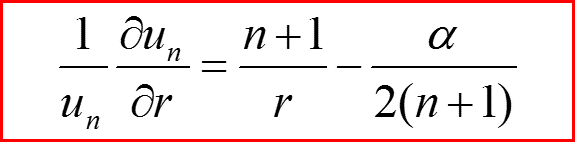
IV. Собственные функции l=n
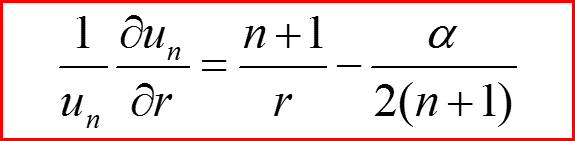
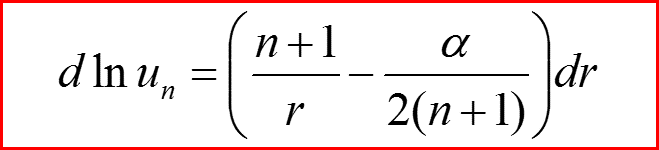
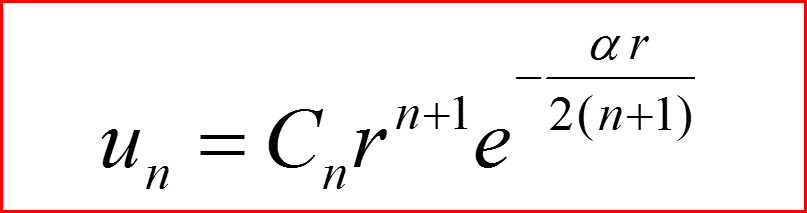
IV. Собственные функции l=n
Уровни энергии атома водорода удобно нумеровать с помощью числа n!
Поэтому волновые функции для уровня l=n ,будем обозначать через unn
При этом одному уровню энергии с заданным n будут соответствовать различные функции: unn,un-1,n,un-2,n,…,u0,n
IV. Собственные функции l=n-1
l=n-1
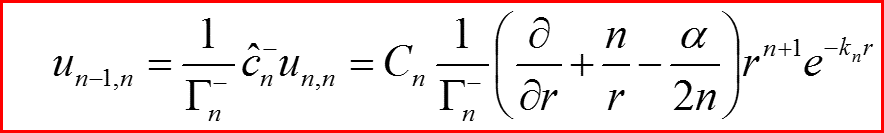
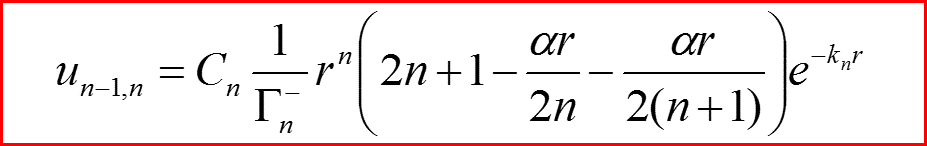
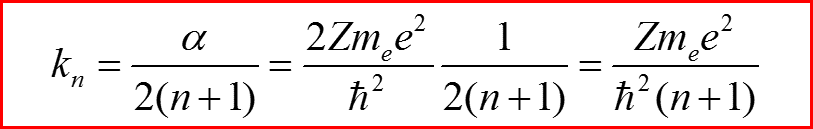
IV. Собственные функции l=n-2
l=n-2
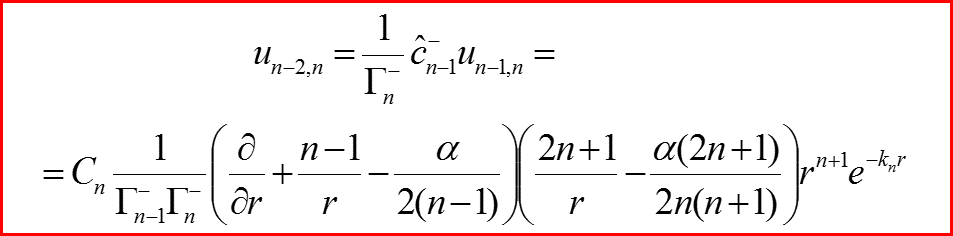
IV. Основное состояние n=0
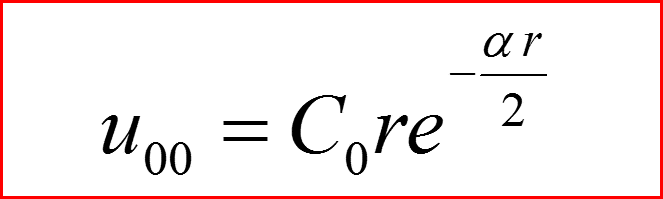
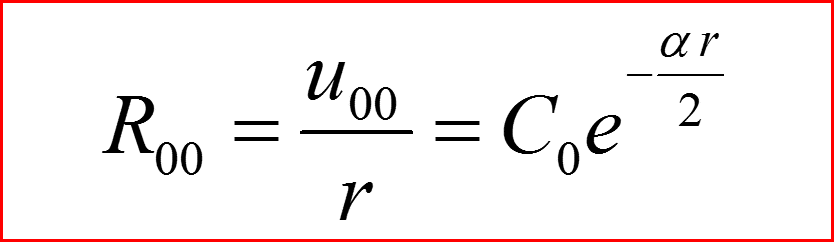
IV. Основное состояние n=0
n=0 Нормировка
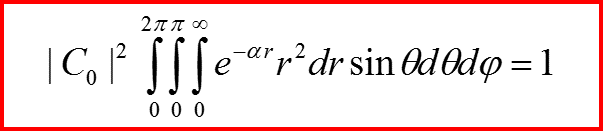
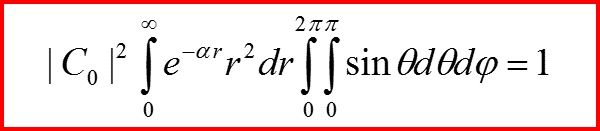
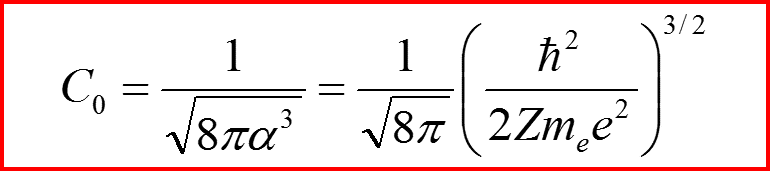
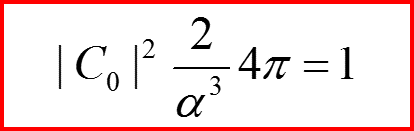
IV. Первое возбужденное состояние n=1
l=1
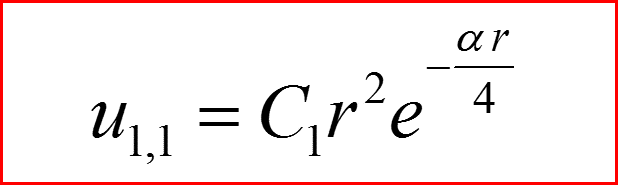
l=0
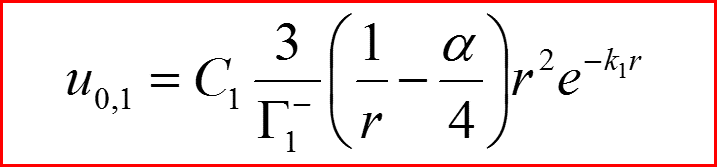
IV. Первое возбужденное состояние n=1
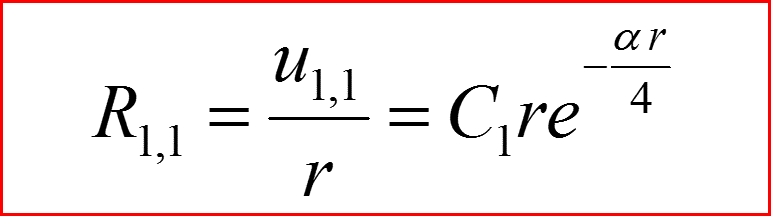
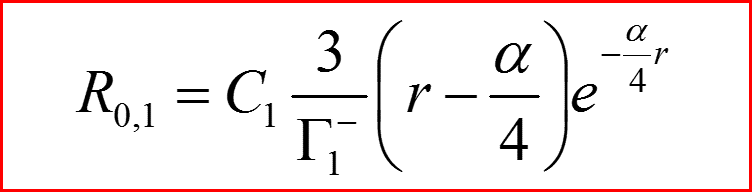
IV. Первое возбужденное состояние n=1. Полный набор
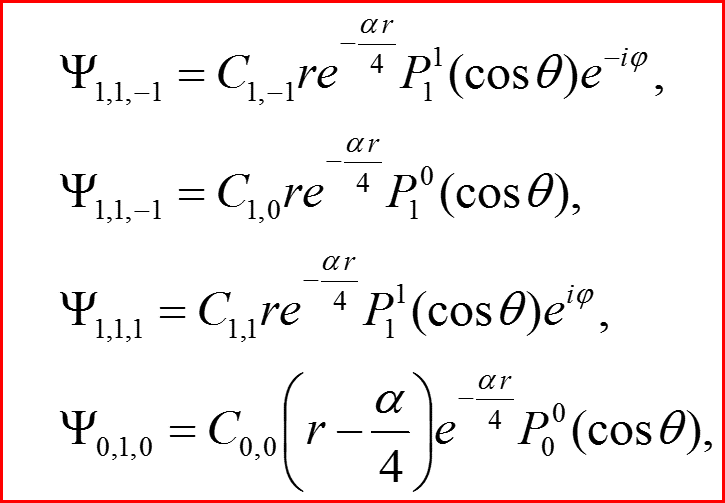
Спектр энергии атома водорода
Метод лестничных операторов
![]()
V. Спектр энергии
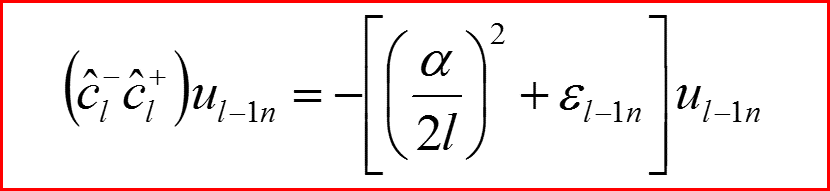
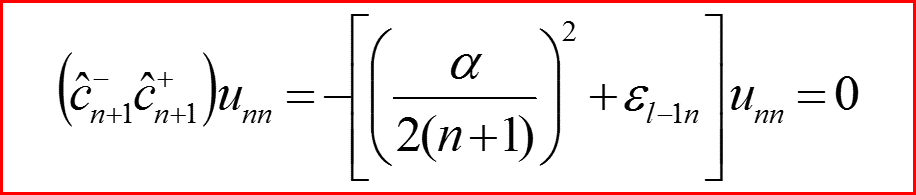
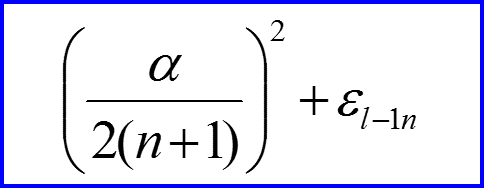
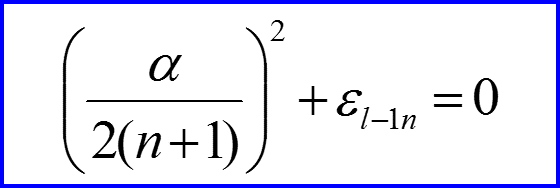
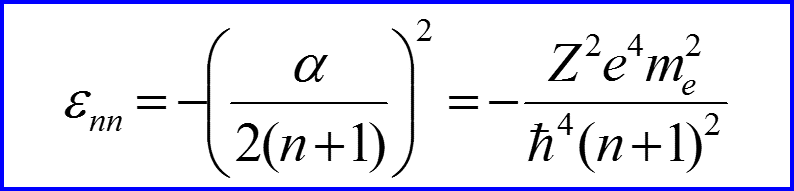
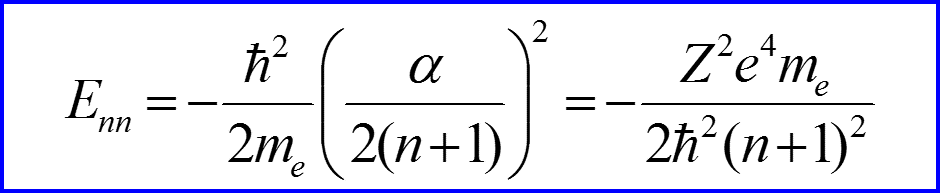
V. Спектр энергии
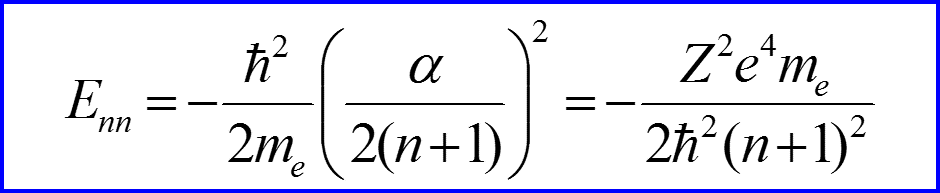
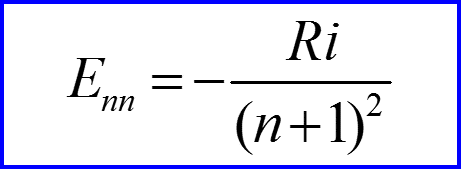
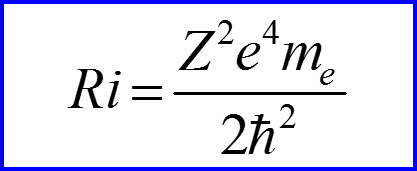
Ri – постоянная Ридберга!!!
Атом водорода. Спектр энергии
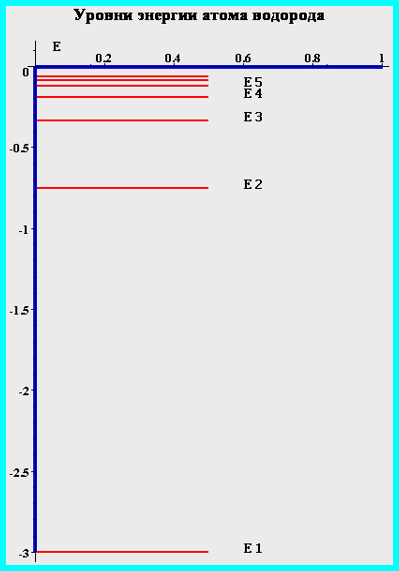
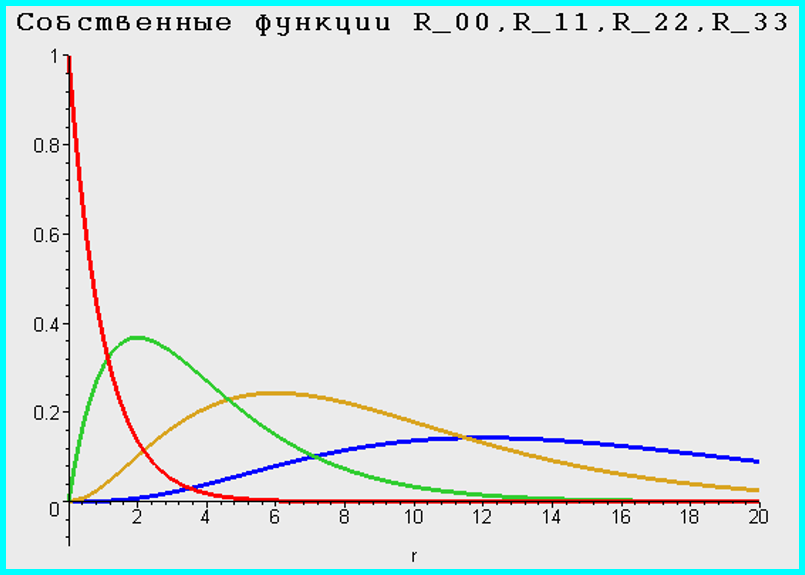
IV. Собственные функции Rnn
Следующая лекция
![]()
Движение в электромагнитном поле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.