Плоское деформированное состояние. (Примеры решения задач)

Глава 7

                ПЛОСКОЕ ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ

                         ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1. Проверить, что формула (7.5) действительно дает главные значения тензора напряжений

                          .

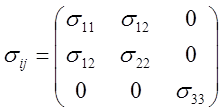если принято условие .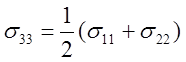

Решение. Главные значения тензора напряжений  определяем из харак­теристического уравнения (2.24), которое в рассматриваемом случае имеет вид:

                      .

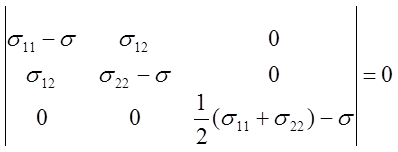Раскладывая определитель по элементам третьей строки, получим:

                

             .

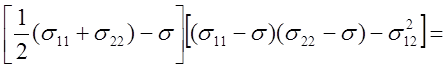
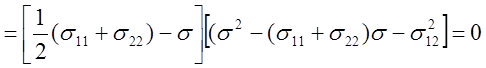Очевидно, что корни этого уравнения следующие:

                                      

             .

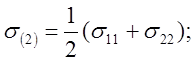
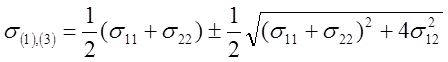2. В процессе штамповки с вытяжкой без трения через квадратную матрицу уменьшение площади сечения составляет 50%. Линии скольжения состоят из ради­альных  прямых — линий  и дуг окружностей — линий  (рис. 42). Сетка линий скольжения заполняет веерообразную область. Определить компоненты скорости вдоль линийи, выраженные через скорость подачи материала и полярные ко­ординаты и.

Решение. Из (7.24) можно получить соотношения:

    на -линии;

    на -линии.

Так как вдоль прямых -линий, то из второй формулы находим  или   . Поскольку нормальная компонента скорости вдоль ВС непрерывна, эта константа в данной задаче должна быть равна  т. е. . Вдоль круговых -линий  и тогда

                              

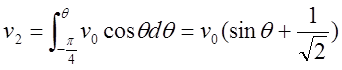
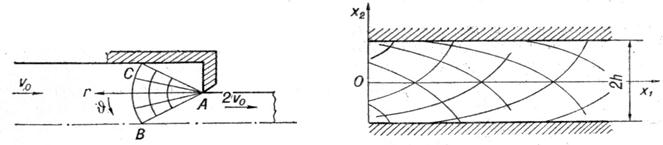
Рис. 42. процесс штамповки с        Рис. 43. Сжатие тонкого слоя меж-  вытяжкой  через квадратную        ду шероховатыми плитами                                            матрицу                                                   

3. Определить поле напряжений и поле скоростей при сжатии пластического слоя между параллельными жесткими и шероховатыми плитами (рис. 43) при толщи­не слоя значительно меньше его протяженности.

Решение. Задача решена Прандтлем и рассмотрена в [12]. Пластический слой выдавливается в стороны и течет от середины к краям. Для развитых пластиче­ских деформаций можно считать, что касательные напряжения на поверхностях кон­такта достигают максимального значения .

Ввиду большой протяженности слоя уравновешивающиеся нагрузки в концевых сечениях слоя не могут существенно влиять на состояние слоя в некотором отдалении от концов. Кроме того, интересны также решения, которые не удовлетворяют точно граничным условиям на торцах слоя.                                     

Напряжения

                            

                                     

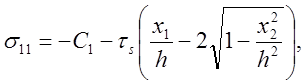
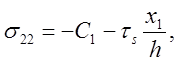
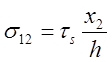
удовлетворяют дифференциальным уравнениям равновесия (7.11) и условию пластич­ности (7.10) при любом значении произвольной постоянной.

Краевое условие на левом торце можно удовлетворить интегрально в смысле принципа Сен-Венана исходя из условия отсутствия нормальной силы на левом торце слоя: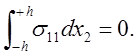

Подставляя в последнее выражение значение  при , находим 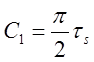и,следовательно,    

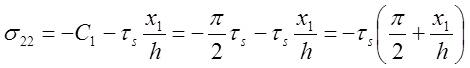                                                                          изменяется по линейному закону на контактной поверхности.

Сила, действующая на слой,

               .

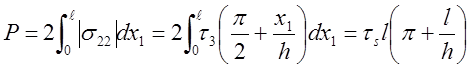Можно показать, что в рассматриваемой задаче линии скольжения представляют' собой семейство циклоид с радиусом производящего круга h ,а прямые являются огибающими этих семейств циклоид.

Компоненты вектора скорости   

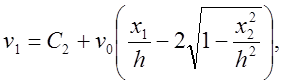
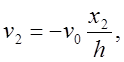                                                 где   — скорость движения плит, удовлетворяют в свою очередь условию несжимае­мости (7.14) и уравнению (7.13) при любых значениях постоянной    .

Постоянная  может быть най­дена из условия равенства потока материала через сечение  ко­личеству, выдавливаемому на длине  при сближении плит: Подставляя в это соотношение при , получим:

Рис. 44. Внедрение плоского штампа в пластическое полупространство

        4. В жесткопластическое тело, ограниченное плоскостью, вдавли­вается со скоростью  абсолютно жесткий штамп с плоским основани­ем (рис. 44). Построить поля напря­жений и установить распределение скоростей.

Решение. Рассматриваемое решение относится  к одним  из самых ранних работ по плоской задаче и было выполнено Прандтлем [12].

Очевидно, что пластические области начинают образовываться в точках А и В сразу же после приложения нагрузки к штампу. В то же время жесткость тела между двумя местными пластическими областями в окрестностях точек А и В вначале ис­ключает вдавливание штампа. Когда нагрузка на штамп достигнет значения, необхо­димого для создания развитой пластической области вдоль всего основания штампа, начнется вдавливание штампа.

Ограничимся рассмотрением начального пластического течения. Построение поля напряжений начнем со свободной поверхности слева от штампа. Участок АЕ должен быть пластическим, чтобы возникла возможность образования выступа над поверхно­стью. Поскольку поверхность свободна от нагрузок. и из (7.10) для точек этой поверхности получим где знак минус взят потому, что в направ­лении АЕ возникает сжатие.

Касательные напряжения на свободной поверхности равны нулю, поэтому ли­нии скольжения пересекают эту поверхность под углами и . Поскольку , следовательно, и  а также  постоянны  вдоль линии АЕ, то из (7.20) следует, что вдоль этой линии параметры  и) не изменяются. Поэтому под линией АЕ поле на­пряжений равномерное.

В соответствии с (7.20), (7.4) и учитывая, что  вдоль линий скольже­ния  (рис. 44) параметр

.

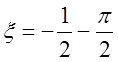Если бы концевая точка Е пластического участка свободной поверхности была из­вестна, то тогда было бы определено равномерное поле напряжений под линией АЕ. Это поле представляло бы собой равнобедренный треугольник ADE.

Поскольку линия скольжения AD представляет собой прямую, то, следовательно, семейство линий скольжения  справа от AD также прямые. Вследствие симметрии задачи заключаем, что под штампом поле напряжений АВС равномерное и, следо­вательно, давление под штампом постоянно.

Таким образом, два равномерных поля напряжений соединены между собой цент­рированным полем ADC. Следовательно, линия скольжения  в поле АЕD является прямой, далее в поле ADC переходит в дугу окружности, которая, в свою очередь, в поле  АВС — опять в прямую. Отсюда следует, что длина пластического участка свободной поверхности равна ширине штампа, т. е. АЕ == АВ = b.

Вдоль линий скольжения  параметр  постоянен. В области АВС линии сколь­жения  наклонены к оси  под углом . Поэтому из формул (7.20) с учетом определенного  ранее параметра 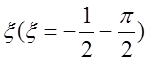  заключаем:

,

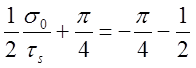откуда                                   .

Подставляя   и   в  (7.17) , имеем:

                       .

Поскольку напряжения вдоль линии  АВ не изменяются, сила, вдавливающая штамп

                           .

Установим далее распределение скоростей. Очевидно, что треугольник АВС движется вниз как жесткое целое со скоростью штампа  . Вдоль линии АС касательная составляющая скорости имеет разрыв, а нормальная равна . Вдоль линии СD касательная составляющая скорости также разрывна, а нормальная равна нулю. В центральном поле скорость в направлении линии скольжения будет равна  , а вдоль линии  равна нулю. Область ADE таким образом скользит как твердое тело в направлении DE со скоростью .