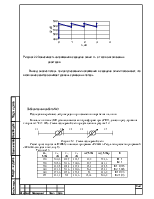
Исходные данные: U=500 кВ, провод 3х(АС-500/64), одноцепные опоры с горизонтальным расположением проводов, расстояние между которыми D=13 м, активное сопротивление R0=0,02 Ом/км, активная проводимость g0 равна нулю.
Решение:
При горизонтальном расположении проводов среднее геометрическое расстояние между проводами:
Dср=1,26·D,
Dср=1,26·13=16,38 м.
,
мм.
При трех проводах в фазе сопротивления и проводимости будут:
,
Ом/км.
,
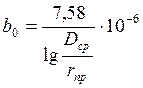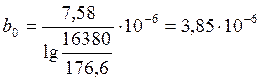1/Ом·км.
Z0=0,02+j0,288=0,288еj86º Ом/км.
Y0=3,85·10-6еj90º 1/Ом·км.
Искомые параметры линии при этом составляют:
1/Ом·км.
α0=1,05·10-3·cos88=3,67·10-5 1/км.
β0=1,05·10-3·sin88·180/π=0,06 град/км.
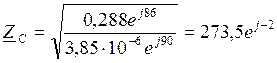Ом.
МВт.
Исходные данные: U=500 кВ, длина линии 900 км выполнена проводами марки 3х(АС-500/64), одноцепные, r0=0,02 Ом/км, g0≈0, х0=0,453 Ом/км, b0=2,497·10-6 1/Ом·км.
Решение:
1) Волновые параметры линии:
,
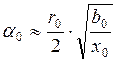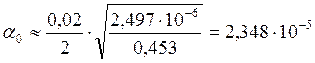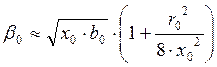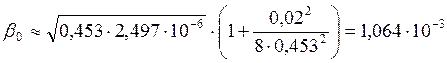1/км.
,
1/км.
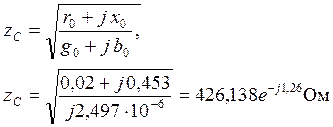
Определим ch g0l и sh g0l по найденным величинам:
a0l=2,348×10 –5×900=0,021,
b0l=1,064×10 –3×900×(180/p)=54,86 0.
chg0l=cha0l×cosb0l+j sha0l×sinb0l ,
chg0l=cos54,86º+j0,021×sin54,86º=0,576+j0,017=0,576×e j1,7º.
shg0=sha0l×cosb0l+jcha0l×sinb0l ,
shg0l=0,021×cos54,86º+j×sin54,86º=0,012+j0,818=0,818×e j89,2º.
Вычисляем обобщённые постоянные:
А=D=chg0l,
А=D=0,576+j0,017=0,576×e j1,7º.
В=zC×shg0l,
В=426,138×е –j1,26º×0,818×e j89,2º=348,57e j87,9=(12,871+j348,339) Ом.
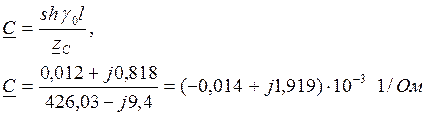
Проверим результаты по условию:
А×D - B×C = 1
(0,576+j0,017)2 –(12,871+j348,339)·(-0,014+j1,919)·10-3 =0,944–j0,031≈1
2) без учёта потерь
Пренебрегая активным сопротивлением линии (r0=0), получим a0=0.
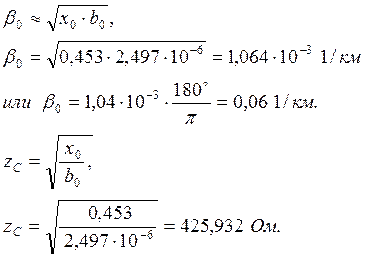
Гиперболические функции для линии без потерь:
chg0l=cosb0l,
chg0l=cos0,06×900=cos54º=0,587.
shg0l=jsinb0l,
shg0l=j×sin54º=j0,809.
Обобщённые постоянные будут иметь вид значения:
А=D=chb0l,
А=D=cos54º=0,576.
В=jzC×shb0l,
В=j425,932·0,809=j344,58 Ом.
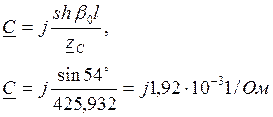
Проверим результаты по условию:
А×D-B×C=1
А×D-B×C =0,5762 – j344,58×j1,92×10 -3 = 0,629+0,604≈1
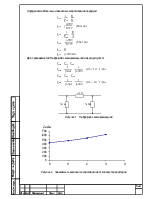
Сравнение результатов расчётов А, В, С, D, и z с учётом и без учёта потерь показывает, что модули волнового сопротивления и обобщённых постоянных в обоих случаях оказывают достаточно близкими по величине. Существенное искажение А, В, С и D от потерь имеет место при больших длинах линий (l > 2000 км). Поэтому для исследования вопросов пропускной способности, перенапряжения, токов коротких замыканий возможно рассматривать вместо реальной линии – идеальную, без потерь.
Требуется определить параметры схемы замещения линии и выбрать мощность реактора по условию выравнивания напряжения в режиме холостого хода.
Решение:
Представим участки линии в виде П-образных схем замещения и найдем поправочные коэффициенты для пересчёта постоянных каждого участка:
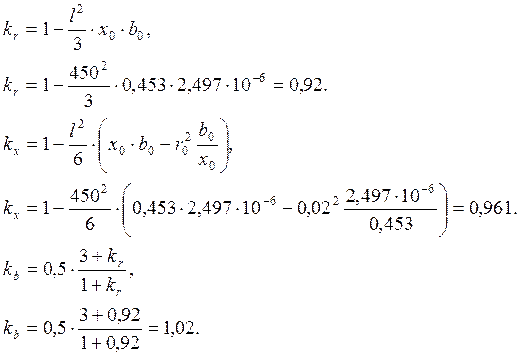
Параметры П-образной схемы замещения участков:
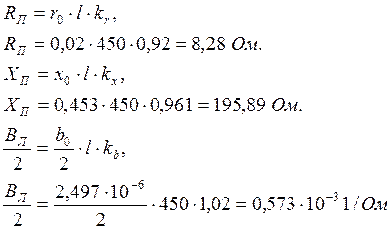
Для выравнивания напряжения в режиме холостого хода суммарная проводимость компенсирующих реакторов должна быть равна проводимости П-образных схем замещения участков в точке их соединения, т.е. в средней точке линии:
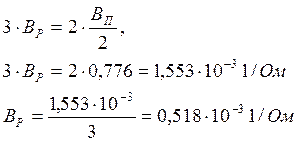
Номинальная мощность одного реактора (3-х фаз)
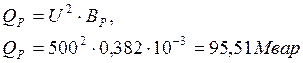
После отключения реакторов представим линию П-образной схемой замещения. Поправочные коэффициенты для пересчёта постоянных линии в этом случае будут:
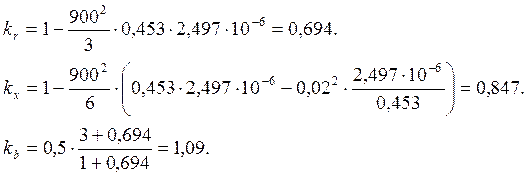
Параметры П-образной схемы замещения всей линии:
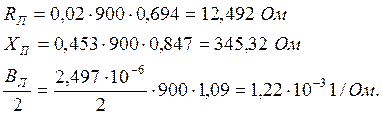
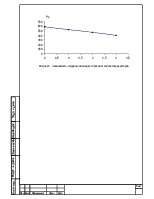
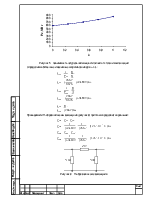
Требуется определить вторичные волновые параметры zв и обобщённые постоянные электропередачи для случаев трех, двух и одного включенных реакторов, а так же собственные и взаимные проводимости и параметры П-образной схемы замещения. Построить графическую зависимость zв=f(n), Рс=f(n), где n-число включенных реакторов.
Решение:
Представим каждую из половин линии в виде четырехполюсника:
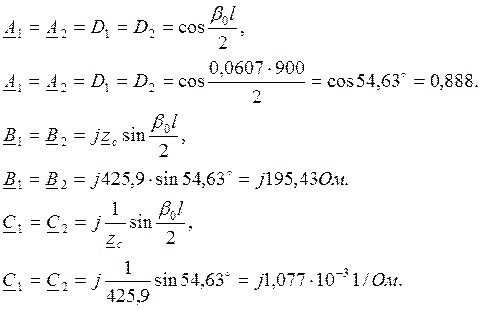
Найдем обобщенные постоянные установки шунтирующих реакторов без учета потерь:
Ар=1; Вр=0; Ср=-jn×Bp; Dр=1;
где n – число включенных реакторов.
Рассматривая последовательное соединение всех трёх звеньев линии, определим матрицу искомых величин:
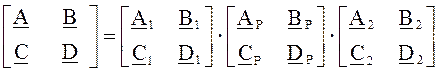
После умножения матрицы получим:
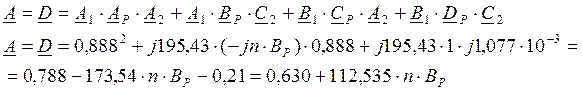
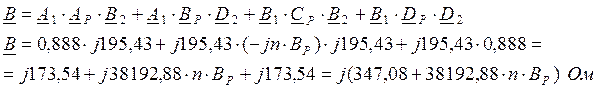
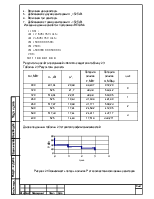
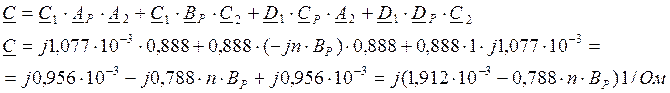Результаты расчётов А,
В, С, D по приведённым формулам показаны в таблице 1.
Таблица 1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.