Расчет параметров линий сверхвысокого напряжения, страница 3

Рисунок 6 – П-образная схема замещения

6.   Линия электропередачи длиной l=900 км.

Требуется определить напряжение в середине линии при передаче мощности Р₂=0,6×Р_с и Р₂=1,5×Р_с МВт и определить фазу напряжения и тока в начале линии. Принять напряжение по концам линии U₁=U₂=500 кВ; r₀=0; z_c=425,932 Ом; P_c= 586,94 9МВт.

Решение

Определим обобщенные постоянные линии:

А=cosb₀l,

А=cos0,06×900=cos54º=0,579.

В=jz_C×sinb₀l,

В=j425,932×sin54º=347,32×е ^{j 90} Ом.

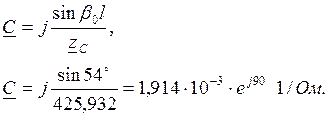
D= А =0,579

1)  Р₂=0,6×Р_с=0,6×586,949=352,17 МВт

Передаваемая мощность в относительных единицах:

Реактивная мощность в конце линии:

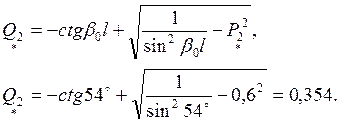
или в именованных единицах,

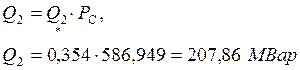
Так как линия работает без перепада напряжения, то реактивная мощность в начале линии равна реактивной мощности в конце и противоположна по знаку. Следовательно

Q₁=-Q₂= -207,86 МВар

Таким образом, поскольку по линии передаётся мощность меньше натуральной (), то она генерирует избыточную реактивную мощность, которую необходимо компенсировать на приёмном и передающем концах (рисунок 7).

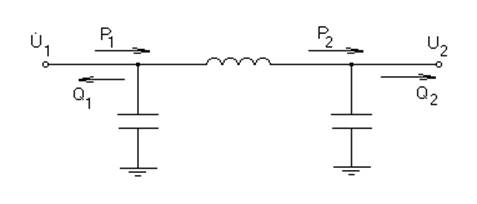
Рисунок 7 – Схема замещения

Угол j₂ между током  и напряжением определяется как:

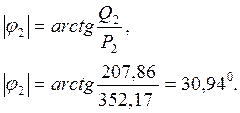
Ток в конце линии:

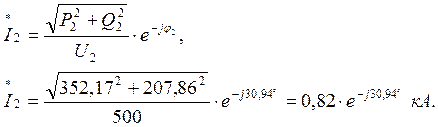
Вектор напряжения  считаем направленным по положительной вещественной оси, т.е. =.

Напряжение в начале линии:

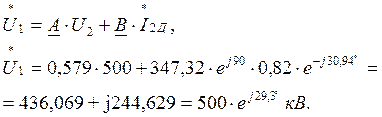
Ток в начале линии:

Следовательно, модуль тока в начале линии равен модулю тока в её конце, а аргумент изменяет знак на противоположный, c изменением своего абсолютного значения.

Определим для половины длины линии обобщенные постоянные:

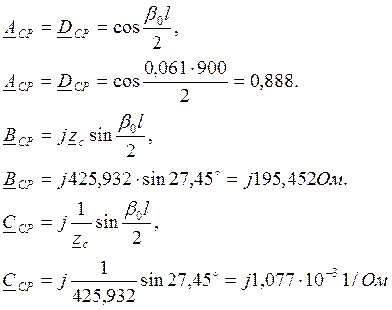
Напряжение в середине линии:

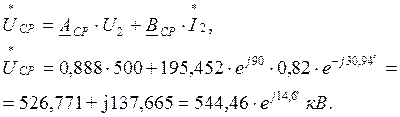
2)  Р₂=1,22×Р_с=1,22×586,949=716,08 МВт

Передаваемая мощность в относительных единицах:

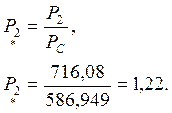
Реактивная мощность в конце линии:

При передаче по линии  мощности, больше натуральной (), в линию необходимо выдавать реактивную мощность с обоих концов.  (рисунок 8).

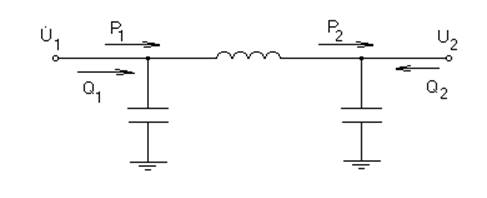
Рисунок 8 – Схема замещения

В именованных единицах реактивная мощность в конце  линии:

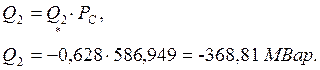
Q₁= - Q₂=368,81 МВАр.

Угол j₂ между током  и напряжением :

.

Ток в конце линии:

Напряжение в середине линии:

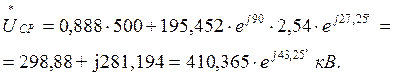
7. Линия длиной l=900 км разомкнута на конце, в начале линии подведено напряжение 500 кВ.

Требуется произвести расчёт распределения напряжения вдоль линии. Построить графическую зависимость напряжения в функции расстояния от начала ЛЭП.

Решение:

В линии разомкнутой с приёмного конца (при I₂=0), напряжение в промежуточных точках определяется из уравнения:

или при А=0,579.                

Откуда

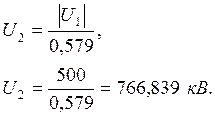
Для середины линии:

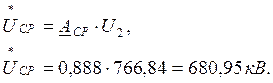
Напряжение для любой промежуточной точки рассматриваемой линии:

где А_х=cos b₀(900-l_x)

l_x –расстояние, отсчитанное от начала линии.

При l_x=150 км:

А_х=cos 0,061×(900-50)=0,617,

Остальные расчёты проводятся аналогично и сводятся в таблицу 5.

Таблица 5

Lx, км	0	50	100	150	200	250	300	350	400	450
Ux, кВ	440,9	473,7	505,1	535,1	563,6	590,4	615,6	639,1	660,7	680,5
Lx, км	500	550	600	650	700	750	800	850	900
Ux, кВ	698,3	714,2	728,1	739,8	749,5	757,1	762,8	765,8	766,8

По данным таблицы 5 строится зависимость U_x=f(l_x) (рисунок 9).

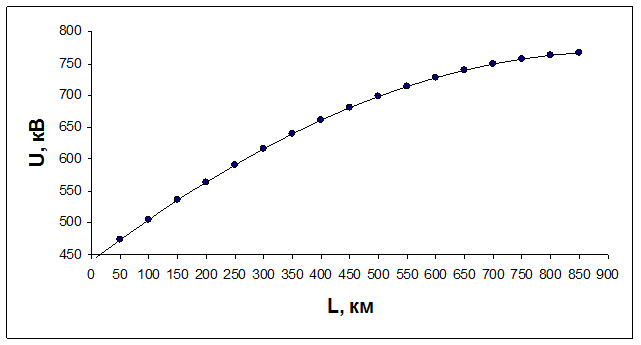
Рисунок 9 – Распределение напряжения вдоль линии, разомкнутой с приёмного конца

8. Участок линии передачи длиной 450 км и напряжением 500 кВ, выполненный проводами марки 3х(АС-500/48), работает с равными напряжениями по концам U₁=U₂=500 кВ.

Требуется построить графические зависимости реактивных мощностей начала и конца участка Q₁, Q₂ от передаваемой активной мощности.

Принимаем обобщенные постоянные участка линии:

А=D=0,576+j0,017=0,576·е^j1,7º,

В=12,871+ j348,3= 348,5×е ^j87,9º Ом.

С= 0,00192·е^-j89.6º.

Решение:

Вычислим комбинации обобщенных постоянных:

Задаваясь мощностью Р₁ от 0 до 700, получим

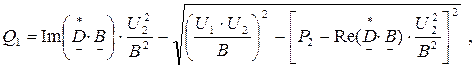
Таблица 6