|
n |
А |
В |
С, 1·10-3/Ом |
D |
|
0 |
0,578 |
J347,1 |
J1,913 |
0,578 |
|
1 |
0,644 |
J361,7 |
J1,612 |
0,644 |
|
2 |
0,711 |
J376,3 |
J1,31 |
0,711 |
|
3 |
0,777 |
J390,9 |
J1,009 |
0,777 |
Для рассматриваемой линии: ![]()
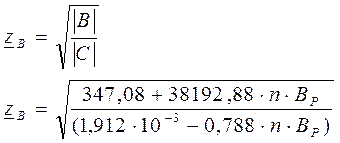
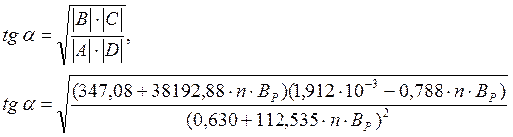
Результаты расчётов zв, a и Рс по приведённым формулам показаны в таблице 2.
Таблица 2
|
n |
0 |
1 |
2 |
3 |
|
Zв,Ом |
425,9 |
473,7 |
535,9 |
622,4 |
|
a |
54,7 |
49,8 |
44,65 |
38,9 |
|
|
586,8 |
527,7 |
466,5 |
401,7 |
Присоединение к линии реакторов приводит к уменьшению электрической длины линии и увеличению электрического сопротивления, что снижает предел передаваемой мощности по линии. Таким образом, присоединение реакторов к промежуточным точкам линии оправдывается лишь при малых нагрузках для выравнивания напряжениях и уменьшения потерь.
Определим собственные и взаимные сопротивления передачи:
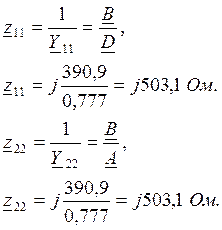
![]()
Для проводимостей П-образной схемы замещения имеем (рисунок 3).
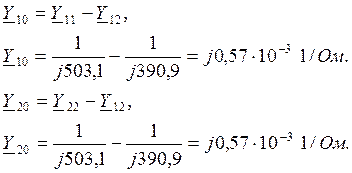
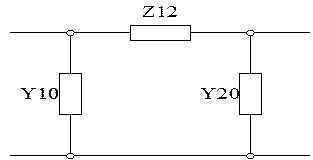
Рисунок 1 – П-образная схема замещения
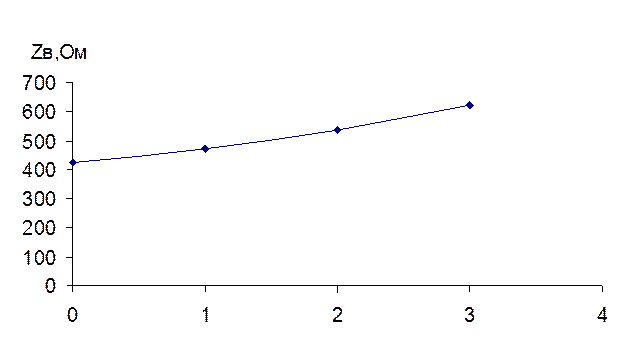
Рисунок 2 – Зависимость волнового сопротивления от количества реакторов

Рисунок 3 – Зависимость натуральной мощности линии от количества реакторов
Требуется определить обобщённые постоянные электропередачи и её вторичные волновые параметры, а так же собственные и взаимные проводимости и параметры П-образной схемы замещения для различных степеней продольной компенсации. Активным сопротивлением линии можно пренебречь. Построить графическую зависимость zв=f(К), Рс=f(К), где К- степень компенсации.
Решение:
Степень продольной компенсации определяется по формуле:
![]()
где Хс – сопротивление установки конденсаторов.
УПК можно представить в виде четырёхполюсника с обобщенными постоянными:
АК=1; ВК=-jк×x0×l; СК=0; DК=1;
Рассматривая последовательное соединение всех трёх звеньев, найдём матрицу обобщенных постоянных:

После умножения матрицы получим:

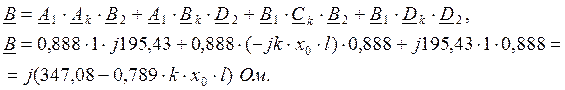
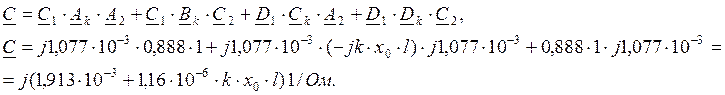 где
l – длина
всей линии, равная 850 км.
где
l – длина
всей линии, равная 850 км.
Результаты расчётов по приведённым формулам показаны в таблице 3.
Таблица 3
|
k |
А |
В |
С×10-3 |
D |
|
0 |
0,578 |
J347,1 |
J1,91 |
0,578 |
|
0,25 |
0,627 |
J306,9 |
J1,97 |
0,647 |
|
0,5 |
0,676 |
J266,7 |
J2,03 |
0,676 |
|
0,75 |
0,724 |
J226,5 |
J2,09 |
0,724 |
|
1 |
0,773 |
J186,3 |
j2,15 |
0,773 |
Из таблицы 3 видно, что увеличение степени продольной компенсации приводит к увеличению постоянной А, и уменьшению постоянной В, что является положительным фактором.
Вторичные волновые параметры линии с УПК найдём по формулам:

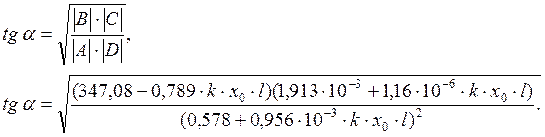
Результаты расчётов zв, a и Рс по приведённым формулам показаны в таблице 4.
Таблица 4
|
k |
0 |
0,25 |
0,5 |
0,75 |
1 |
|
Zв,Ом |
425,9 |
394,5 |
362,38 |
329,212 |
294,45 |
|
a |
54,6 |
51 |
47,5 |
43,5 |
39,3 |
|
|
586,8 |
633,7 |
689,9 |
759,4 |
849 |
По рисункам 4 и 5 видно, что с увеличением степени компенсации существенно улучшаются волновые параметры линии электропередачи.
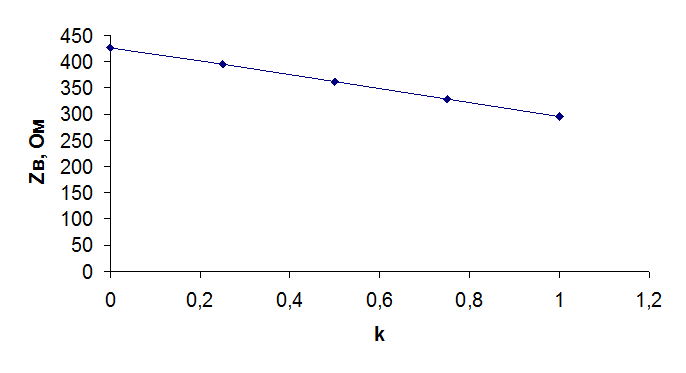
Рисунок 4 – Зависимость волнового сопротивления от степени компенсации

Рисунок 5 – Зависимость натуральной мощности линии от степени компенсации
Определим собственные и взаимные сопротивления для k=0,5:

![]()
Проводимости П-образной схемы замещения (рисунок 6) при этом определяются равными:
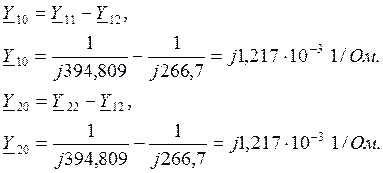
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.