Основные законы электростатики и постоянного тока: Методические указания и контрольные задания к контрольной работе № 3 по физике. Часть 2, страница 4

, где q - заряд обкладки. Знак “минус” в формуле поставлен в соответствии с принятым в физике соглашением о том, что положительным считается поток вектора, “вытекающего” из замкнутой поверхности наружу. Таким образом, при изображенном на рис. 7 направлении векторов D, E₁ и E₂, заряд обкладки, окруженной поверхностью 1-2-3-4-1, отрицателен. Емкость же, по определению (13), не зависит от знака этого заряда, так как знак заряда, относительно которого отсчитывается разность потенциалов U, всегда совпадает со знаком U. Далее последовательно подставляем в (13) найденные ранее значения q, D и E

.

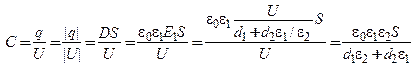Окончательно заключаем, что при заполнении конденсатора диэлектриком его емкость(14) увеличится в

 раза.

Посмотрим еще раз на полученный нами результат, для наглядности переписав его в виде

  .

Сравнивая это выражение с (14), видим, что заполнение пространства между обкладками конденсатора двумя слоями диэлектрика толщиной d₁  и d₂  с диэлектрическими проницаемостями e₁  и e₂  эквивалентно наличию двух конденсаторов с емкостями c_i=e₀e_iS/d_i  (i=1,2) , которые подсоединены последовательно (41). Исследование емкости при объемном заполнении конденсатора двумя диэлектриками предстоит тем, кто будет решать задачу 330.

И, наконец, определим поверхностную плотность зарядов на границе раздела диэлектриков. Поскольку, в отличие от обкладок конденсатора, свободные заряды на этой поверхности отсутствуют, то применим теорему Гаусса в форме (23). Для этой цели выделим на границе раздела диэлектриков участок площадью s , окружим его замкнутой поверхностью 5-6-7-8-5 (рис. 7) и рассчитаем поток вектора напряженности поля E через эту поверхность. Поток через боковую поверхность 5-6 и 7-8 равен нулю, поскольку вектор E направлен по касательной к ней. Потоки через торцевые поверхности 6-7 и 8-5 определяются через напряженности полей E₁ и E₂ в первом и втором слое диэлектрика соответственно, поэтому из (23)

, где s^связи есть искомая плотность зарядов. Обратите внимание, что в обозначениях  рис. 7 вектор  E₁ “вытекает” из поверхности 5-6-7-8-5 , а вектор E₂ - “втекает” в нее. Таким образом, если верхняя по рис. 7 обкладка заряжена отрицательно, то поверхностная плотность зарядов на границе раздела диэлектриков

s^связ  = e₀ (E₁ - E₂) = 8.85 *10^-12 *(4 *10⁴ - 8 *10⁴) = - 354 нКл/м²  тоже отрицательна.

Пример 5. Расположенный вертикально плоский конденсатор, имеющий прямоугольные обкладки с расстоянием между ними d =2 мм, нижней частью погружен в трансформаторное масло плотностью  r = 900 кг/м³ и диэлектрической проницаемостью  e = 2.2 (рис. 8). Конденсатор подключен к источнику постоянного напряжения U=5000 В. На какую высоту h  поднимется масло в конденсаторе?

Решение. Причиной втягивания диэлектрика внутрь конденсатора является появление поляризационных зарядов на поверхности этого диэлектрика. Знаки заряда какой-либо обкладки и поляризационного на ближайшей к этой обкладке поверхности диэлектрика противоположны друг другу и, следовательно, притягиваются. Хотя на первый взгляд кажется, что силовые линии вектора напряженности электрического поля E приводят только к деформации (растягиванию) диэлектрика,  однако это справедливо лишь внутри конденсатора, в области высокой однородности поля (рис. 9). На краях конденсатора электрическое поле неоднородно и