Основные законы электростатики и постоянного тока: Методические указания и контрольные задания к контрольной работе № 3 по физике. Часть 2

26. Сопротивление R системы проводников, состоящей из N звеньев с сопротивлениями R_k :

а) при последовательном соединении

  ;                                         (39)

б) при параллельном соединении

  .                                        (40)

27. Наличие конденсатора в цепях постоянного тока эквивалентно разрыву данного участка цепи. При этом напряжение U на обкладках конденсатора совпадает с разностью потенциалов между узлами данного участка цепи, а заряд q на обкладках определяется формулой (13). Емкость С батареи конденсаторов, состоящей из N конденсаторов с емкостями С_k :

а) при последовательном соединении

  ;                                       (41)

б) при параллельном соединении

  .                                         (42)

Примеры решениЯ задаЧ

Пример 1. На покоящуюся частицу массы m=1г с зарядом q=20 мкКл налетает точно такая же, имевшая на бесконечности скорость v₀=150 м/с. Движение происходит вдоль прямой, проходящей через частицы. Определить минимальное расстояние r_min, на которое сблизятся частицы.

Решение. Поскольку расстояние минимального сближения частиц не зависит от системы отсчета, перейдем в так называемую систему центра инерции, в которой суммарный импульс частиц равен нулю. Эта система отсчета движется в том же направлении, что и налетающая частица, со скоростью v₀/2. Задача становится симметричной относительно обеих частиц (рис. 2).

m      v                 v     m q                                               q r      Рис. 2. Сближение частиц в системе центра инерции

В произвольный момент времени частицы находятся на расстоянии r друг от друга и каждая из них обладает скоростью v, направления которых противоположны. Энергия W системы двух частиц состоит из кинетической и потенциальной:

  .

При записи потенциальной энергии мы воспользовались формулами (3) и (5) для потенциала точечного заряда. Поскольку трения в задаче нет, энергия системы частиц не меняется в течение всего процесса. Запишем выражения для энергии в начальный момент времени, когда потенциальной энергией можно пренебречь, и в момент минимального расстояния между ними, когда их скорости (а значит, и кинетические энергии) обращаются в нуль; и приравняем эти энергии друг к другу:

  .

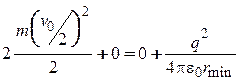Окончательно получаем

  .

Пример 2. Четыре заряда связаны пятью нитями длиной L=0.1 м каждая так, как показано на рис.3. Заряды, находящиеся в противоположных вершинах ромба, попарно равны друг другу:  q₁=q₃=2 мкКл и q₂=q₄=1.5 мкКл. Определить силу натяжения нити, связывающей заряды q₂ и q₄ .

Решение. Из симметрии задачи ясно, что достаточно рассмотреть равновесие только двух любых смежных зарядов. Выберем для этой цели q₁ и q₂ . Аккуратно рисуем все действующие на эти заряды векторы сил (рис. 4). Углы обозначаем по ходу решения по мере необходимости.

Условия равновесия выбранных зарядов формулируются в виде равенства нулю векторной суммы сил, действующих на каждый из зарядов:

  ;

  , где  (i,k=1,2,3,4) - силы Кулона, действующие на i-й заряд со стороны k-го,  (i,k=1,2,3,4) - силы натяжения нитей, действующие на i-й заряд вдоль нити, соединяющей его с k-м.

Из симметрии задачи заключаем, что равны друг другу модули сил натяжения нитей:

 T₂₃ = T₂₁ ;

T₁₂ = T₁₄

и модули сил Кулона

F₂₃ = F₂₁ ;

F₁₂ = F₁₄ .

Перейти к следующим умозаключениям о равенстве модулей сил позволяет нам третий закон Ньютона:

T₁₂ = T₂₁ ;

F₁₂ = F₂₁ .

Далее вводим оси координат (рис. 4) и переписываем два векторных условия равновесия в четыре скалярных для проекций векторов на оси x и y :

 - проекции на ось x сил, приложенных к точке 2 ;

 - проекции на ось x сил, приложенных к точке 1 ;

 - проекции на ось y сил, приложенных к точке 2 ;

 - проекции на ось y сил, приложенных к точке 1 .

Обратите внимание, что перед проекцией каждого вектора стоит знак “+”, если она совпадает по направлению с направлением выбранных нами осей координат, и “-” - в противоположном случае. Первое и последнее из этих четырех уравнений не несут ничего нового, ибо являются тривиальными следствиями установленных ранее из симметрии и третьего закона Ньютона равенств. Второе и третье же, с учетом этих равенств и школьной формулы cos(p/2-a)=sina , переписываются в виде:

2 F₁₂ sin a + F₁₃ - 2 T₁₂ sin a= 0;

2 F₁₂ cos a+ F₂₄ - 2 T₁₂ cos a - T₂₄ = 0.