Указание. Координаты произвольной точки полости охарактеризуйте радиус-вектором, соединяющим центр шара с этой точкой. Далее воспользуйтесь формулами (7).
Пример 4. Площадь обкладок плоского конденсатора S=20 см2, расстояние между обкладками d=7.5 мм. Во сколько раз изменится емкость конденсатора, если пространство между обкладками заполнить двумя слоями диэлектрика толщиной d1=5 мм и d2=2.5 мм с диэлектрическими проницаемостями e1=6 и e2=3 соответственно? Определить напряженность и смещение электрического поля в каждом из слоев диэлектрика, а также поверхностную плотность зарядов на границе раздела диэлектриков, если конденсатор заряжен до напряжения U=400 В.
|
E1 D1 e1 d1 d
Рис. 6. К решению примера 4 |
||||||||||||||||||||||||||||||||
Решение (рис. 6). Хоть это и не понадобится в дальнейшем, из любопытства подсчитаем начальную емкость незаполненного диэлектриком конденсатора(14):
C0=e0S/d=8.85*10-12*0.002/
/0.0075=2.36 пФ .
Электрическая индукция (смещение) D не зависит от количества связанных зарядов в диэлектрике и, следовательно, одинакова для обоих слоев диэлектрика (20):
D1 = e0 e1 E1 = e0 e2 E2 = D2 . (a)
Кроме того, сумма падений напряжения на обоих слоях диэлектрика U1 и U2 должна совпадать с напряжением между обкладками U. Для тех, кому не очевидно это утверждение, поясним, что электрические силы потенциальны; другими словами, работа этих сил по замкнутому контуру равна нулю. Если же выбрать контур так, чтобы внутри конденсатора он был перпендикулярен обкладкам и далее замыкался за пределами конденсатора, то работа по перемещению единичного заряда по этому контуру равна U1 + U2 - U = 0, что и доказывает сказанное. Итак (9),
U = E1 d1 + E2 d2 . (б)
Формулы (а),(б) представляют систему уравнений для определения напряженностей полей в диэлектриках. Откуда
|
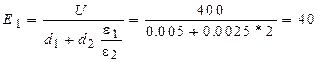
|
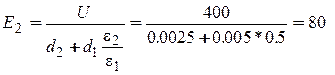
Индукция электрического поля
D = e0 e1 E1 = e0 e2 E2 = 2.12 мкКл/м2 .
|
1 E1 D e1 4 d1 d 6 7 E2 D 5 8 e2 d2 Рис. 7. Выбор замкнутых поверхностей для применения теоремы Гаусса |
Для вычисления емкости конденсатора по формуле (13) необходимо знать величину свободных зарядов на его обкладках. Применим теорему Гаусса в форме (22): окружим одну из обкладок замкнутой поверхностью 1-2-3-4-1 (рис. 7) и рассчитаем поток вектора смещения D через эту поверхность. Поток через боковую поверхность 1-2 и 3-4 равен нулю, поскольку вектор D направлен по касательной к ней; через торец 2-3 потока также нет, поскольку величина вектора D за пределами конденсатора пренебрежимо мала, по сравнению с таковой внутри конденсатора. Отличный от нуля поток индукции электрического поля есть только через торцовую поверхность 4-1 , поэтому из (22)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.