Основные законы электростатики и постоянного тока: Методические указания и контрольные задания к контрольной работе № 3 по физике. Часть 2, страница 2

Неизвестными величинами в этих уравнениях являются T₂₄ и T₁₂ , причем T₂₄ - это та самая величина, которую требуется определить по условию задачи. Угол известен: a = 60°. А силы Кулона легко определяются из исходных данных по формуле (1). Чтобы избавиться от T₁₂ в системе уравнений, можно, например, домножить первое из них на cos a , второе - на sin a и вычесть их друг из друга

F₁₃ cos a - F₂₄ sin a + T₂₄ sin a = 0.

Отсюда

T₂₄ = F₂₄  - F₁₃ ctg a.

Отметим, что решение в таком виде остается справедливым при любой длине нити L₂₄  между зарядами q₂ и q₄, лишь бы выполнялись условия неотрицательности правой части последней формулы и L₂₄ < 2L . Осталось подставить заданные по условию величины:

;      ;

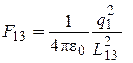, где  - расстояние между зарядами q₁ и q₃.

Ответ имеет вид:

 .

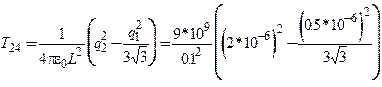Пример 3. Тело имеет форму шара радиуса R = 0.2 м. В нем вырезали сферическую полость радиуса r = 0.04 м, центр которой находится на расстоянии a = 0.08 м от центра сферы, однородно заряженной с объемной плотностью r= 2 мкКл/м³. Найти напряженность E электростатического поля вдоль луча, проходящего из центра шара через центр полости. Вычислить напряженность поля в точке этого луча, лежащей на границе шара.

Решение. Вдоль радиуса шара, проходящего через центр полости, проведем координатную ось Ox, где O - центр шара, x>0  - координата произвольной точки (рис.5).

Для решения воспользуемся принципом суперпозиции (10), а именно: представим, что есть два заряженных тела- сплошной шар радиуса R, однородно заряженный с объемной плотностью r и маленький шарик радиуса r, также однородно заряженный, но противоположного знака, т.е. с объемной плотностью -r. При этом мы будем считать, что шарик находится внутри большого шара так, что расстояние между их центрами равно a, т. е. в пределах объема маленького шарика их заряды взаимно компенсируются. Нетрудно видеть, что такая модель эквивалентна исходной задаче.

Воспользовавшись определением объемной плотности заряда для большого шара

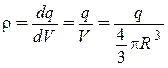, перепишем формулу для напряженности электростатического поля (7) сплошного шара вдоль оси Ox в виде

при   0 £ x < R  ,

при    x ³ R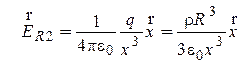  , где  - вектор, проведенный из точки O в точку x.

Введем также вектор  - длиной a и направленный из центра большого шара (точки O ) в центр маленького. Тогда формулы для напряженности маленького шарика отличаются от приведенных знаком объемной плотности и сдвигом (на ) центра:

   при a - r £ x £  a + r                       ,

при 0 £ x £  a-r и при a+r £ x£ R.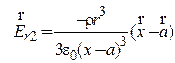

Принцип суперпозиции (10) гласит, что напряженность электрического поля системы зарядов равна векторной сумме напряженностей полей от каждого из них. Откуда следует, что E(x) - непрерывная кусочно-гладкая функция, имеющая на различных интервалах области определения следующий аналитический вид:

при   0 < x < a - r 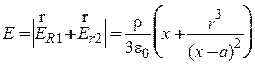       , поскольку в этом интервале  ;

при a - r < x < a + r  ;

при a + r < x < R        , поскольку в этом интервале    ;

при R < x               .

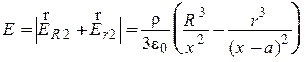При   x = R       .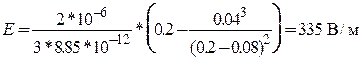

В качестве упражнения попробуйте доказать, что поле внутри полости однородно.