










имеет составляющую, втягивающую диэлектрик в конденсатор с некоторой силой F (рис. 9).
|
Ee F ----------------++++++++++++ Рис. 9. Чертеж силовых линий напряженности E электричес-кого поля |
Введем y и z - размеры обкладок конденсатора, в соответствии с выбранными на рис. 8 осями координат, тогда S=yz - площадь обкладки конденсатора, а Sd=yzd - объем конденсатора. Напряженность электрического поля в конденсаторе E=U/d (4) при постоянной разности потенциалов U между обкладками не зависит от наличия или отсутствия в нем диэлектрика. До контакта с диэлектриком электрическое поле пустого конденсатора обладало запасом потенциальной энергии (24)
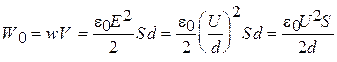 .
.
Если бы конденсатор был отключен от источника напряжения, то эта энергия не изменилась бы и после втягивания диэлектрика внутрь конденсатора, величина свободных зарядов на обкладках также была бы постоянной. Анализ такой ситуации предстоит тем, кто будет решать задачу 343. В условии же нашего примера источник напряжения совершает работу A =UDq, где Dq - величина изменения заряда на обкладках, равная в соответствии с (13) и (14)
![]() .
.
Обратите внимание, что работа A источника всегда положительна.
Запишем закон сохранения энергии в виде
W0 +A =W +Wж , где W - энергия электростатического поля конденсатора после наполнения его диэлектриком; Wж - механическая потенциальная энергия жидкого диэлектрика. Потенциальная энергияW поля частично заполненного конденсатора находится по формуле (24):
![]() .
.
Таким образом, закон сохранения энергии позволяет вывести формулу для механической энергии столба жидкости в диэлектрике:
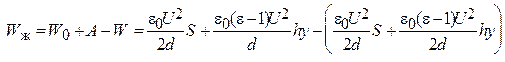 , или, приводя подобные члены,
, или, приводя подобные члены,
![]() .
.
Эта энергия должна равняться по модулю работе сил F (рис. 8), втягивающих диэлектрик в конденсатор:
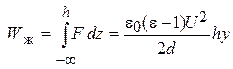 .
.
Дифференцируя последнее равенство по h, получим:
![]() .
.
Ясно, что в условиях равновесия эта сила совпадает с силой гидростатического давления жидкости на глубине h :
F = mg = rgdhy, где m = rV = rdhy - масса втянутого диэлектрика. Приравнивая друг другу полученные выражения для силы, окончательно получим:
![]() .
.
Пример 6. Площадь обкладок плоского конденсатора S=20 см2, расстояние между обкладками d=7.5 мм. Пространство между обкладками заполнено двумя слоями слабопроводящего диэлектрика толщиной d1=5 мм и d2=2.5 мм с диэлектрическими проницаемостями e1=6 и e2=3 и удельными проводимостями б1 = 60 пСм/м и б2 = 40 пСм/м соответственно? Определить напряженность, смещение электрического поля, плотность тока и плотность тепловой мощности тока в каждом из слоев диэлектрика, а также поверхностную плотность зарядов на границе раздела диэлектриков, силу тока через конденсатор, мощность этого тока и сопротивление конденсатора, если он подключен к источнику постоянного напряжения U=400 В.
|
E1 j1 D1 б1 e1 d1 d
Рис. 10. К решению примера 6 |
|||||||||||||||||||||||||||||||||||||||||||||||
Решение (рис. 10). В условиях стационарного протекания электрического тока плотность тока одинакова для обоих слоев слабопроводящего диэлектрика. Это утверждение является прямым следствием закона сохранения заряда (а в стационарных условиях заряд нигде накапливаться не может) и носит название условия неразрывности линий тока. Следовательно, из закона Ома (28)
j1 = б1 E1 = б2 E2 = j2
(в скобках заметим, что столь простой вид уравнения получился и благодаря постоянству сечения проводника S; если бы площади слоев отличались друг от друга S1 ¹S2 , то следовало бы писать более общее условие постоянства полного тока (33): j1 S1 = б1 E1 S1 = =б2 E2 S2 = j2 S2 ). Кроме того, сумма падений напряжения на обоих слоях диэлектрика U1 и U2 должна совпадать с напряжением между обкладками U (ср. с примером 4). Откуда, воспользо-вавшись (9), получим
U = E1 d1 + E2 d2 .
Неизвестных величин в записанных уравнениях - две: E1 и E2 , уравнений - тоже два. Находим:
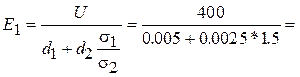 45.7 кВ/ м;
45.7 кВ/ м;
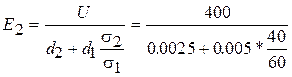 = 68.6 кВ/ м.
= 68.6 кВ/ м.
Вновь обращаясь к закону Ома в дифференциальной форме (28), определяем плотность тока j1 =j2 в конденсаторе:
j1 =j2 = б1 E1 = б2 E2 =2.74 мкА/м2 .
Индукция (смещение) электрического поля определяется для каждого из слоев диэлектрика по формуле (20):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.