Некоторые дифференциальные модели турбулентности, страница 4

Такой подход практически неприменим к течениям с сильным изменением свойств среды поперёк слоя, течениям около пористой поверхности, при наличии сильных градиентов давления и ряде других осложняющих факторов. Поэтому в последние годы большое значение уделяется так называемым моделям для течений с низкими турбулентными числами  . В них «константы» модели (например С₁, С₂ и С_m) являются функциями числа , учитывающими влияние молекулярной диффузии, что позволяет проводить расчет вплоть до стенки. При этом граничные условия задаются непосредственно на основе физического смысла. Так например, , так как турбулентные пульсации затухают на стенке.

Особое внимание в настоящее время уделяется моделям напряжений Рейнольдса. Эти модели лишены недостатков всех упомянутых выше моделей, поскольку не используют гипотезу Буссинеска. В то же время использование таких моделей требует решения, по меньшей мере, пяти  дополнительных дифференциальных уравнений, что делает их мало применимыми для инженерных приложений. Более того, для ряда членов, входящих в уравнения для напряжений Рейнольдса, необходимо введение в модель дополнительных гипотез, справедливость которых остается в настоящий момент недоказанной.

С более подробным сравнением различных моделей турбулентности можно познакомиться в многочисленных обзорах, например [6, 7, 17…20].

Надо отметить, что уравнения переноса, в частности, уравнения для к и , а также для любого из напряжений Рейнольдса имеют одинаковую структуру. Это объясняется тем, что переменные (составляющие скорости, кинетическая энергия турбулентности, скорость диссипации, температура или энтальпия, массовые концентрации химической составляющей и др.) выводятся или из одного закона сохранения, или из подобных ему законов. Отсюда следует важное свойство, позволяющее существенно упростить процедуру расчета уравнений переноса. Обозначив любую из перечисленных выше зависимых переменных буквой , можно получить так называемое «транспортное» уравнение [21]. В наиболее общей векторной форме оно выглядит так:

    ,              (7.8)

где  – коэффициент переноса;  – источниковый член.

Конкретный вид  и  зависит от смысла переменной . В таблице приведены конкретные значения  и  для двумерного плоского течения несжимаемой жидкости при использовании модификации [19] модели .

Уравнение			S
– неразрывности	1	0	0
– U – компоненты           скорости	U
– V – компоненты          скорости	V
– энергии, записанное    через энтальпию	H		0
– кинетической энер-    гии турбулентности	к
– диссипации кинети-    ческой энергии тур-    булентности	e

В приведенных в таблице соотношениях использованы следующие значения констант и функций:

,  ,   ,  ,  ,

,.

При этом турбулентная вязкость вычисляется по формуле

,

где 

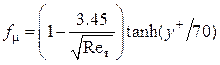
Тензорная запись обобщенного уравнения в декартовой системе координат имеет вид:

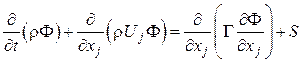,              (7.9)

где индекс  в соответствии с тремя пространственными координатами принимает значения 1, 2, 3.

Процедура записи дифференциального уравнения в обобщенном виде заключается в его преобразовании до тех пор, пока нестационарный, диффузионный и источниковый члены уравнения для данной зависимой переменной не примут стандартный (канонический) вид. Тогда за выражение для  принимают коэффициент перед  в диффузионном члене, а оставшиеся члены в правой части обозначают буквой  (источниковый член).