Некоторые дифференциальные модели турбулентности, страница 3

Модели с одним дополнительным уравнением применимы лишь к течениям или областям течений, которым соответствуют достаточно большие значения локального турбулентного числа Рейнольдса . Следовательно, они неприменимы вблизи стенки и вязкий подслой необходимо рассматривать с помощью пристеночных функций.

Наибольшее развитие получили дифференциальные модели с двумя дополнительными уравнениями. Чаще всего в них решается уравнение для кинетической энергии турбулентности к и еще для одного параметра (например, масштаба длины , скорости диссипации , временного масштаба  и др.)

Широкоизвестной моделью турбулентности второго приближения является ()-модель турбулентности, предложенная Колмогоровым и Прандтлем. В ней помимо осредненных уравнений Рейнольдса использованы два дополнительных дифференциальных уравнения для турбулентной энергии к и масштаба турбулентности .

Для турбулентной вязкости использовалось соотношение (7.3).

Для получения замкнутой системы уравнений необходимо иметь уравнение для определения масштаба . В задаче свободной турбулентности используют гипотезу Прандтля , где  – полуширина зоны смешения на основном участке струи. В более сложных течениях для определения  выводят дополнительное дифференциальное уравнение.

Модель Колмогорова – Прандтля использовалась для расчета пограничного слоя и свободных струйных течений.

Одной из наиболее популярных является ()-модель турбулентности, предложенная Харлоу (1968). Эта модель по существу – вариант модели Колмогорова-Прандтля. В ней вместо неизвестного масштаба  использованы дифференциальное уравнение переноса диссипации турбулентной кинетической энергии  и связь (7.2).

Соотношение (7.2) исключает из рассмотрения . Турбулентная вязкость при этом

                                ,                                          (7.4)

а турбулентное трение

                                       .                                        (7.5)

При использовании этой модели дополнительно к уравнениям для осредненного течения привлекают уравнения переноса кинетической энергии турбулентности  к  и скорости ее диссипации , которые для плоских течений имеют вид:

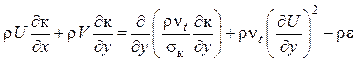.          (7.6)

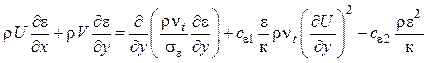.   (7.7)

Эти уравнения содержат пять постоянных, для которых в результате проведенного комплекса контрольных расчетов выбраны следующие значения:

;   ;    ;    ;   .

Указанные константы обеспечили удовлетворительные результаты расчетов для плоских течений. Для осесимметричных, затопленных и спутных струй приведенные значения констант давали плохое согласование расчета с экспериментом, что привело к необходимости введения соответствующих поправок.

Следует отметить, что приведенные выше уравнения для к и  справедливы только в области, достаточно удаленной от стенки, где числа  велики и влияние молекулярной вязкости пренебрежимо мало по сравнению с турбулентной вязкостью. Для типичных пограничных слоев это означает, что . Для задания граничных условий часто используют пристеночные функции (Launder, 1974), которые позволяют определить значения всех параметров на некотором расстоянии от стенки, которое больше, чем толщина вязкого подслоя. В соответствии с этим методом предполагаем, что распределение скорости подчиняется логарифмическому закону и турбулентность находится в локальном равновесии, т. е. генерация турбулентности равна ее диссипации. С помощью этих предположений устанавливаем связь между скоростью, кинетической энергией турбулентности, скоростью диссипации и другими параметрами течения.