Завесы на адиабатической и неадиабатической поверхностях. Теплообмен в зоне завесы

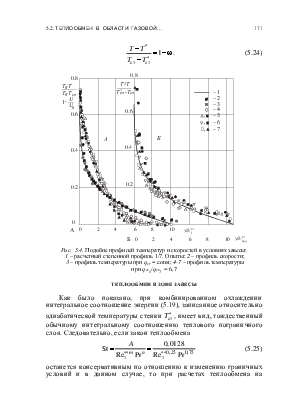
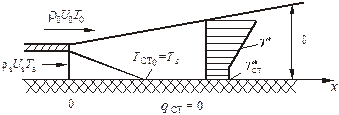
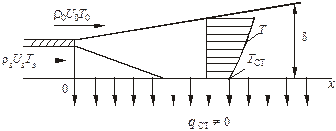
Рис. 5.3. Схемы завес на адиабатической и неадиабатической

поверхностях

Если определять  по разности , то возникает вопрос о влиянии на теплоотдачу различных параметров газовой завесы: величины вдува, высоты щели, коэффициента восстановления и др. Это потребовало бы проведения достаточно широких исследований.

Эккерт и Жестков предложили определять коэффициент теплоотдачи в области газовой завесы формулой, аналогичной выражению для нахождения коэффициента теплоотдачи при течении газа с большими скоростями:

    .                                 (5.14)

Здесь – температура адиабатической стенки. Эта гипотеза предполагает, что общее решение дифференциального уравнения энергии получается наложением двух решений, одно из которых учитывает заградительное охлаждение стенки, другое – регенеративное охлаждение.

Рассмотрим пристенный пограничный слой. Тепловой пограничный слой на участке  формируется одним из способов организации газовой завесы. Для области  коэффициент теплоотдачи будем определять по формуле (5.14). Получим интегральное уравнение энергии в области действия газовой завесы ().

Уравнение теплопроводности в рассматриваемых условиях  запишем обычным способом:

.                            (5.15)

В случае газовой завесы на адиабатической поверхности ()

                   .                          (5.16)

Вычитая из (5.15) уравнение (5.16) с учетом уравнения неразрывности, получаем

          .         (5.17)

Интегрируя это уравнение по толщине пограничного слоя с учетом граничных условий:

при    ,  ,  ,  ,

при     ,     ,  

имеем

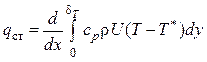                    .                      (5.18)

Это уравнение подобно обычному уравнению энергии теплового пограничного слоя и переходит в него при отсутствии тепловой завесы (). После несложных преобразований (5.18) получается интегральное уравнение энергии пограничного слоя газовой завесы на неадиабатической поверхности

                  .                     (5.19)

Как видно, по форме оно совпадает с обычным уравнением теплового пограничного слоя, но в этом случае

                                    ,                                     (5.20)

а толщина потери энергии

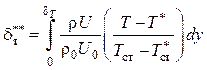                         ,                         (5.21)

где  и – температуры в рассматриваемой точке пограничного слоя с газовой завесой соответственно при отсутствии и наличии теплообмена на стенке.

Для обычного пограничного слоя  толщина потери энергии

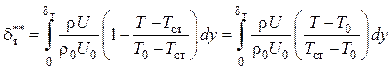 .        (5.22)

Было экспериментально определено подобие профилей температур и скоростей на примере ступенчатого подвода тепла к стенке. Вторую ступень можно рассматривать как находящуюся в области завесы со стороны первой ступени. Профили температуры при наличии теплообмена в области газовой завесы были измерены и обработаны двумя способами. При первом способе они представлены в виде безразмерной избыточной температуры относительно температуры невозмущенного потока

,

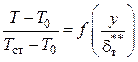при этом толщина потери энергии рассчитывалась по выражению (5.22). В такой обработке данные показаны на рис. 5.4, поз. а. Они сопоставлены с профилем дефекта скорости и расчетом по степенной зависимости :

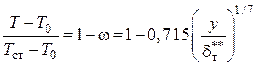                .                   (5.23)

Как видно, в такой обработке наблюдается существенное неподобие профилей скоростей и температур.

На рис. 5.4, поз. б те же самые экспериментальные данные обработаны вторым способом: относительно адиабатической температуры в рассматриваемой точке пограничного слоя , которая представляет собой профиль температуры в условиях газовой завесы на адиабатической стенке. В этом случае толщина потери энергии  определялась выражением (5.21). При такой обработке сохраняется подобие полей скоростей и температур при наличии теплообмена в зоне завесы

                              .                                      (5.24)

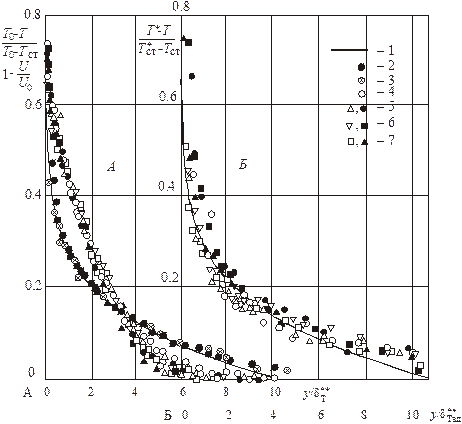
Рис.  5.4. Подобие профилей температур и скоростей в условиях завесы:

 1 – расчетный степенной профиль 1/7. Опыты: 2 – профиль скорости;

 3 – профиль температуры при q_ст = const; 4-7 – профиль температуры

при q_ст1/q_ст2  = 6,7

Теплообмен в зоне завесы

Как было показано, при комбинированном охлаждении интегральное соотношение энергии (5.19), записанное относительно адиабатической температуры стенки , имеет вид, тождественный обычному интегральному соотношению теплового пограничного слоя. Следовательно, если закон теплообмена

                                                 (5.25)

останется консервативным по отношению к изменению граничных условий и в данном случае, то при расчетах теплообмена на поверхности в области завесы коэффициент теплоотдачи в форме (5.14) можно определять обычным способом.

Консервативность (5.25) подтверждена в опытах при ступенчатом подводе теплоты к стенке. Опыты проводили в два этапа. Сначала теплоту подводили только к первой ступени . При этом на поверхность вниз по потоку (вторая ступень) воздействовала тепловая завеса со стороны первой ступени. Измеряли температуру газа в пограничном слое  и температуру адиабатической стенки . Затем подводили тепло на второй ступени .

Опытные данные о теплообмене на второй ступени обрабатывали двумя способами. В первом  случае числа Стентона и Рейнольдса определяли по разности температур стенки и невозмущенного потока

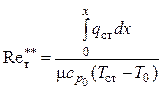,    .                 (5.26)

Экспериментальные данные в такой обработке сопоставлены с законом теплообмена (5.25) (рис. 5.5), откуда видно, что в удовлетворительном соответствии с расчетом находятся только те опыты, в которых отношение тепловых потоков . В этих опытах вследствие слабого теплообмена на первой ступени адиабатическая температура стенки  близка к температуре невозмущенного потока . При  наблюдается существенное отклонение опытов от расчета. Таким образом, этот способ обработки не позволяет обобщить экспериментальные данные в области тепловой завесы.

При обработке вторым способом коэффициент теплоотдачи и толщину потери энергии находили по разности  и :

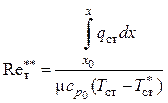,   .          (5.27)

Поскольку процесс теплообмена на второй ступени происходит в уже развившемся пограничном слое, при определении числа Стентона учитывали влияние начального динамического слоя по формуле

.

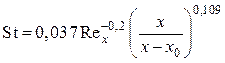В такой обработке опытные данные удовлетворительно согласуются с законом теплообмена (5.25) (рис. 5.5).