Завеса в градиентных потоках и соплах

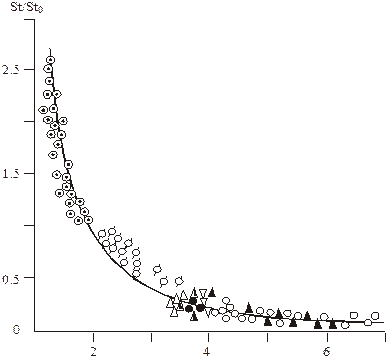
Рис. 5.10 . Влияние  неизотермичности  на  тепломассообмен

в условиях завесы. Сопоставление расчета с экспериментом

Видно, что теоретическая формула (5.70) удовлетворительно согласуется с экспериментом во всем исследованном диапазоне изменения фактора неизотермичности ,  ,  и неоднородности вдува газа .

5.5.   Завеса в градиентных потоках и соплах

Тепловой пограничный слой по сравнению с динамическим консервативен по отношению к продольному градиенту давления. С увеличением положительного градиента давления (диффузорные течения) профили скорости сильно деформируются, снижаются коэффициенты трения. Профили же температур почти не изменяются, и коэффициенты теплообмена не зависят от величины градиента давления вплоть до зоны отрыва, если опыты обрабатывают по локальным параметрам потока.

Отрицательный градиент давления также практически не влияет на закон теплообмена до значения параметра ускорения потока , характеризующего возможное начало его ламинаризации.

Рассмотрим газовую завесу на плоской теплоизолированной стенке, когда скорость в ядре потока  является функцией продольной координаты (рис. 5.11).

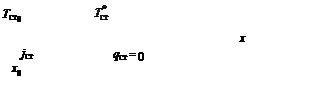
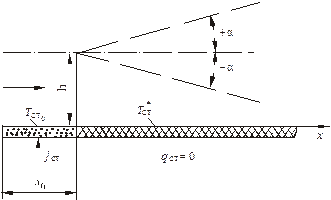
Рис. 5.11. Схема завесы в градиентном потоке

Из уравнения энергии на теплоизолированной части стенки

                                                            (5.77)

получаем следующее соотношение для эффективности тепловой завесы:

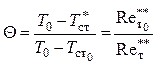.                               (5.78)

В случае  безградиентного течения для определения коэффициента , учитывающего деформацию профиля температур на адиабатической стенке, использовалась толщина потери импульса. При градиентном течении она зависит от величины градиента давления и поэтому коэффициент  удобнее выразить через толщину потери энергии :

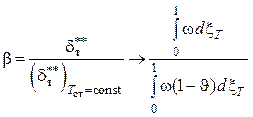                  ,                     (5.79)

где ,   .

При степенных профилях скорости  и температуры  и при условии  из (5.79) получаем

                               .                                (5.80)

Для безградиентного и конфузорного течения (при ) , а для предотрывного диффузорного (, )   .

Из интегрального соотношения энергии пограничного слоя при

                                            (5.81)

получаем следующее выражение:

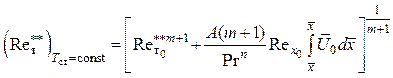     ,        (5.82)

где ,    .

Тогда для течения с переменной скоростью на внешней границе пограничного слоя из (5.77), (5.79) и (5.82) можно получить интерполяционную формулу для эффективности завесы

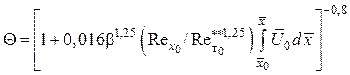            .           (5.83)

Здесь  – число Рейнольдса, построенное по параметрам в конце участка охлаждения, и зависит от способа организации завесы.

При течении в каналах, образованных плоскими стенками, скорость на внешней границе пограничного слоя изменяется по закону

                                 ,                               (5.84)

где  – начальная высота канала;  – угол наклона стенки. Тогда формула (5.83) для эффективности завесы в таких каналах  для конфузорного течения (при ) имеет вид

                                 ,                               (5.85)

где

.              (5.86)

Изменение эффективности газовой завесы за участком пористого вдува по длине канала для разных углов наклона стенки показано на рис. 5.12 (в первичной обработке).

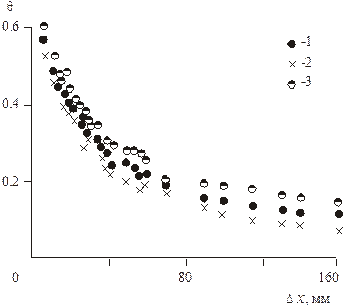
Рис. 5.12. Влияние угла наклона стенки на эффективность

завесы:  1 – a = 0^о,  2 – a = – 15^о,  3 – a = +15^о

Видно, что в одинаковых условиях на входе положительный градиент давления увеличивает эффективность газовой завесы, а отрицательный – уменьшает.

Опыты при конфузорном течении в плоском канале с наклонной стенкой  хорошо обобщаются с учетом изменения скорости по длине и согласуются с расчетом (5.85) (рис. 5.13).

В области умеренных положительных градиентов давления будет справедлива формула (5.85), учитывающая изменение скорости вдоль поверхности. В этом случае для диффузорного предотрывного течения  и получаем следующее выражение для эффективности завесы:

                                 .                               (5.87)

А₁

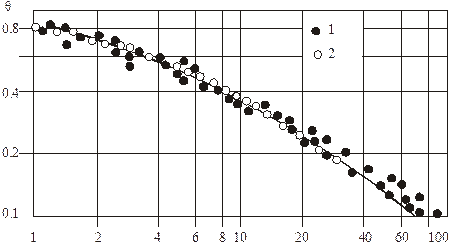
Рис. 5.13. Обобщение опытов при конфузорном течении

При безотрывном течении в пограничном слое опыты удовлетворительно  согласуются с (5.85) и (5.87). С увеличением угла раскрытия диффузора и интенсивном вдуве через пористый участок эффективность завесы может резко ухудшиться (см. рис. 5.14), что объясняется ростом размеров отрывной зоны вниз по потоку за задней кромкой проницаемого участка. Это подтверждают измерения профилей скоростей.

Положение точки отрыва наступает раньше при больших пористых вдувах. Увеличение же скорости тангенциального вдува повышает устойчивость течения.

А₁

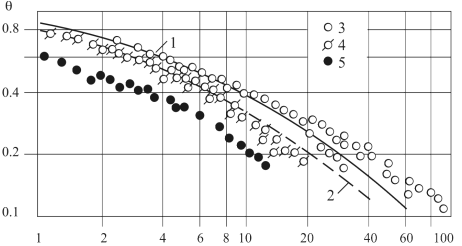
Рис. 5.14. Эффективность завесы при диффузорном течении

1, 2 – расчеты по (5.85) и (5.87); 3…5 – опыты

Эффективность завесы при течении в соплах