Теплообмен в пристенной струе. Газовая завеса с переменными физическими свойствами

Важным предельным случаем щелевого заградительного охлаждения является затопленная струя, взаимодействующая с поверхностью, когда скорость спутного потока равна нулю () или мала по сравнению со скоростью вдува . Схема рассматриваемого течения показана на рис. 5.6.

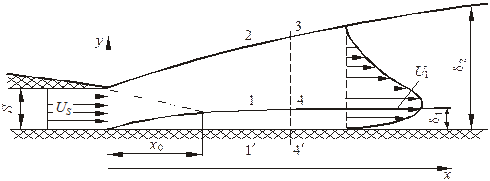
Рис. 5.6. Схема течения затопленной пристенной струи

Для элемента струи  толщиной  уравнение импульсов имеет вид

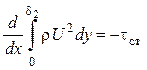                             .                                 (5.28)

Разбиваем пределы интегрирования

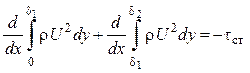                  .                      (5.29)

Силы трения на внешней границе пограничного слоя равны нулю (при ,    и  ), для контура 1–2–3–4 можно записать следующее уравнение импульсов:

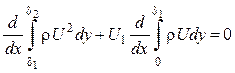                      ,                        (5.30)

где  – скорость на внешней границе пристенного пограничного слоя. Производная во втором члене (5.30) есть масса, проходящая  через сечение 1–4. Изменение массы от сечения  до сечения , т. е. на расстоянии , происходит только за счет добавки массы, которая проходит через сечение 1–4. Из уравнения (5.30) следует, что

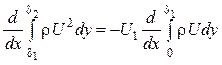.                       (5.31)

Это уравнение связывает изменение импульса во внешней части струи с импульсом, вносимым в пристенный пограничный слой присоединяемой к нему массой жидкости из области .

С учетом (5.31) уравнение (5.29) имеет вид

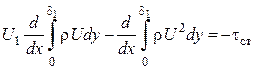                     .                    (5.32)

Введем величины, характерные для пристенного пограничного слоя  и :

,      .

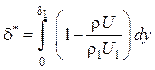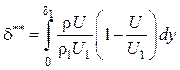Тогда уравнение (5.32) приводится к виду

 ,                   (5.33)

или

              .            (5.34)

Здесь ,  ,  ,

,   ,    .

Уравнение (5.34) отличается от обычного уравнения импульсов тем, что помимо формпараметра  содержит в себе еще отношение толщины пограничного слоя к толщине потери импульса . Кроме того, следует обратить внимание на то, что наличие этих формпараметров и величины  в данном случае не связано с градиентом давления, который в дозвуковой затопленной струе практически равен нулю.

При степенном распределении скоростей в пристенном пограничном слое по закону степени

.         (5.35)

Уравнение (5.34) можно получить также, интегрируя уравнение движения пограничного слоя по оси  от  до :

 ,                                    (5.36)

учитывая уравнение неразрывности

                                                                                (5.37)

и граничные условия

                ,

        .

Полагаем, что законы трения и теплообмена сохраняют консервативность и в рассматриваемом случае течения. Тогда для квазиизотермического течения несжимаемого газа уравнение (5.34) с учетом закона трения запишется в виде

                                     (5.38)

(для :,  , ).

Поскольку толщина пристенного пограничного слоя во много раз меньше толщины струи   (Г.Н. Абрамович), закон изменения максимальной скорости в пристенной струе можно принять таким же, как и в свободной струе с начальным сечением 2 (скорость на стенке при отсутствии трения):

                                   .                               (5.39)

Уравнение (5.39) хорошо подтверждено в опытах Майерса, Шауэра, Юстиса и Сигаллы.

Уравнение (5.38) – линейное дифференциальное уравнение типа Бернулли. Интегрируя его от  до  при условии , имеем

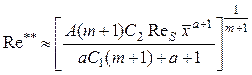                        .                     (5.40)

Подставляя (5.40) в степенной закон трения, имеем:

– по скорости   

,                (5.41)

                                ;                           (5.42)

– по скорости  

.                   (5.43)

На начальном участке:

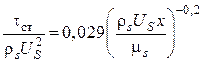                             .                        (5.44)

Полагая для турбулентного потока подобие

                                 ,                               (5.45)

находим коэффициенты теплообмена:

а) для затопленной струи, распространяющейся вдоль поверхности в пространстве, затопленном покоящейся жидкостью:

                  ,                   (5.46)

                  ;                 (5.47)

б) при наличии слабого спутного потока

              .          (5.48)

Сопоставление формул (5.46), (5.48), (5.43) с опытами показано на рис. 5.7 и 5.8.

Напомним, что при обтекании потоком пластины коэффициент теплообмена определяется по формуле

                        .                                (5.49)

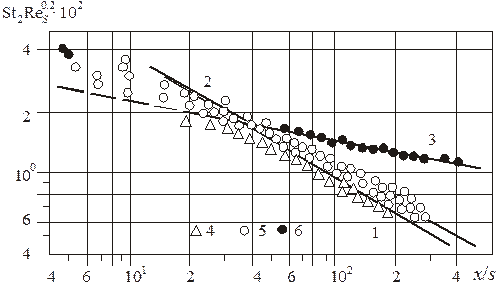
Рис. 5.7. Теплообмен в пристенной струе:

1 – расчет по (5.46), 2 – (5.48), 3 – (5.49), 4 – 6 – опыты

(5.43)

(5.44)

 

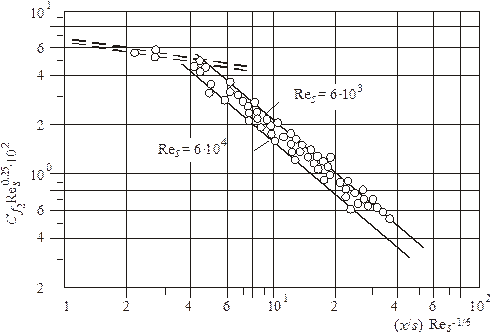
Рис. 5.8. Коэффициент трения в затопленной пристенной струе.

Сопоставление с опытами Майерса

5.4.  Газовая завеса с переменными

        физическими свойствами

Рассмотрим процессы турбулентного тепломассообмена в условиях газовой завесы при воздействии поперечного потока вещества на стенке, неизотермичности, неоднородности состава газа, сжимаемости. Теоретический анализ будет основан на использовании асимптотической теории турбулентного пограничного слоя С.С. Кутателадзе и А.И. Леонтьева.

Относительные законы теплообмена

В турбулентном ядре пограничного слоя плотность теплового потока в соответствии с формулой Прандтля можно выразить следующим образом:

                                        ,                                         (5.50)

где ,  – скорость и энтальпия в рассматриваемой точке пограничного слоя;  и – длина гидродинамического и теплового пути смешения. Считаем, что влияние пульсации плотности на перенос количества движения и теплоты отсутствует .

При течении газов, когда подобны граничные условия и , можно принять также подобие профилей скоростей и полных энтальпий. Как мы показали ранее, при наличии газовой завесы условие подобия выполняется, если профили относительных энтальпий (температур) строить с учетом их адиабатических значений (т. е. значений в рассматриваемой точке пограничного слоя в условиях завесы на адиабатической стенке):

                            .                         (5.51)

Здесь  и  – теплосодержание газа на стенке при наличии теплообмена  и без него ;  и  – теплосодержание газа в рассматриваемой точке пограничного слоя при наличии газовой завесы на неадиабатической и адиабатической стенках.

Условие (5.51) подтверждается опытными данными при . При заградительном охлаждении адиабатической стенки, когда  вследствие турбулентного перемешивания происходит выравнивание энтальпий внутри пограничного слоя. При этом наибольшая интенсивность турбулентного перемешивания наблюдается в пристенной области, где градиент скорости  имеет максимальное значение. Поэтому деформация профиля энтальпий происходит таким образом, что область с  интенсивно размывается от стенки в глубь пограничного слоя и увеличивается зона с . Этот процесс выравнивания энтальпии в окрестности адиабатической поверхности символически можно записать:

при           .                          (5.52)

Если воспользоваться этим допущением, подобие профилей скоростей