Завеса в градиентных потоках и соплах, страница 2

Рассмотрим заградительное охлаждение осесимметричных сопел Лаваля с адиабатическими стенками (рис. 5.15). В отличие от течения в плоском канале в сопле на эффективность завесы воздействуют сильный отрицательный градиент давления, сжимаемость потока (число Маха), скачки уплотнения на нерасчетных режимах течения.

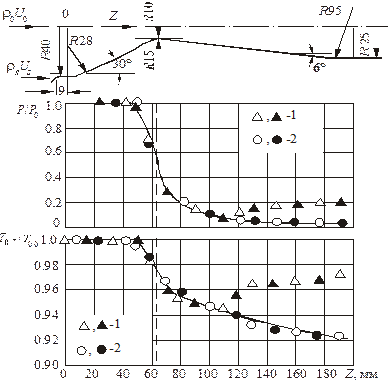
Рис. 5.15. Распределение статического давления и равновесной

температуры стенки по длине сверхзвукового сопла:

1 – течение со скачками уплотнения;  2 – без скачков

Показано, что щелевой вдув воздуха в дозвуковую часть сопла не влияет на коэффициент восстановления температуры на стенке и на распределение статического давления, которые хорошо описываются теорией для одномерного изоэнтропического течения.

Равновесная температура стенки  отличается от температуры торможения потока  вследствие диссипации энергии в пограничном слое, что учитывается коэффициентом восстановления температуры на стенке :

               .                 (5.88)

Статическое давление соответствует расчету

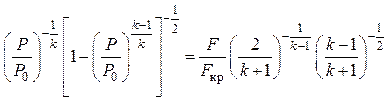      .         (5.89)

Эффективность газовой завесы в сверхзвуковом осесимметричном сопле определяется из интегрального соотношения энергии на теплоизолированной части стенки сопла ()

                                        (5.90)

и имеет вид

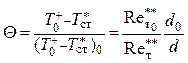                          ,                            (5.91)

где – равновесная температура стенки при течении без завесы.

Характерное изменение эффективности завесы по длине сопла показано на рис. 5.16. Отчетливо просматривается различный характер изменения  в до- и сверхзвуковой областях. Замедление падения эффективности в сверхзвуковой части объясняется влиянием сжимаемости потока, которое усиливается с ростом числа Маха по длине сопла ( на выходе ).

Опыты показали, что увеличение градиента скорости снижает эффективность завесы (рис. 5.17)

Получим соотношение для расчета эффективности газовой завесы  в сверхзвуковом осесимметричном сопле.

В адиабатических условиях () профиль температуры в пограничном слое отличается от профиля температуры в условиях теплообмена. Это приводит к изменению толщины потери энергии и соответственно числа  в (5.91). Число , построенное по толщине потери энергии на адиабатической стенке, можно получить с помощью соотношения

                            .                                (5.92)

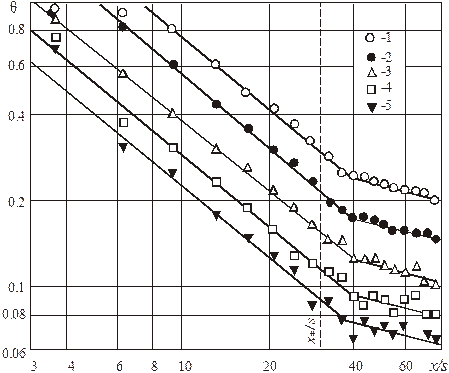
Рис. 5.16.  Изменение  эффективности  завесы  в  дозвуковой

и сверхзвуковой областях сопла при разных параметрах вдува m

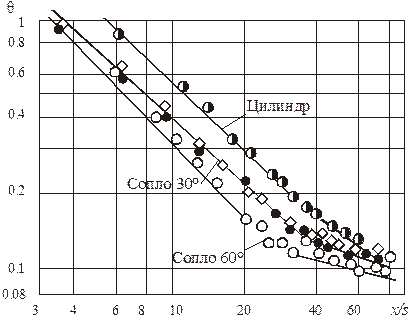
Рис. 5.17. Влияние градиента скорости на эффективность

завесы в соплах. Полууглы сужения равны 0°, 30°, 60°

Число  находим из решения уравнения энергии для случая, когда существует теплообмен на стенке при условии . При этом число Стентона  в уравнении энергии определяем с учетом влияния неизотермичности и сжимаемости газа

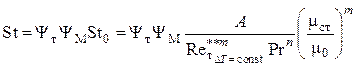         .           (5.93)

В результате получаем интерполяционную формулу для определения   числа  Рейнольдса  ,  рассчитанного  по толщине потери энергии на теплоизолированной стенке сопла при течении с завесой:

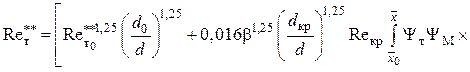
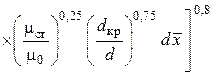.                      (5.94)

На рис. 5.18 показано изменение толщины потери энергии при наличии газовой завесы. Опыты сопоставляем с расчетом (5.94) при , что соответствует условиям завесы на адиабатической стенке. Здесь же приводим расчет при  для теплообмена при . Как видно, в адиабатических условиях толщина потери энергии нарастает значительно интенсивнее, чем в условиях теплообмена, расчет с учетом  удовлетворительно описывает эксперимент.

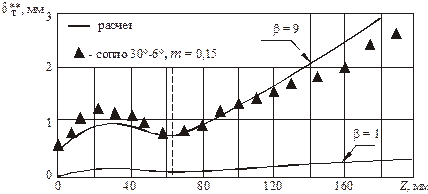
Рис. 5.18. Толщина потери энергии на адиабатической

стенке сопла с завесой

Окончательное выражение для эффективности завесы на теплоизолированной стенке при осесимметричном течении в сопле получаем из соотношений (5.91) и (5.94):

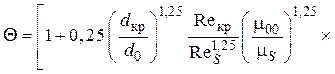
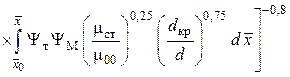.                     (5.95)

Опыты с разными углами сужения в осесимметричных и плоском соплах удовлетворительно согласуются с (5.95). Это показано на рис. 5.19.

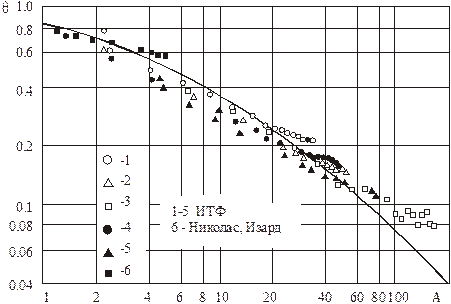
Рис. 5.19. Обобщение опытов в соплах Лаваля

Следует заметить, что использование для расчета эффективности газовой завесы в соплах Лаваля зависимости для пластины

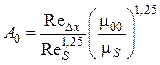,          ,           (5.96)

, в которой значение  определяется по локальным параметрам потока (скорости  и плотности  газа в рассматриваемом сечении сопла), не позволяет получить удовлетворительного обобщения опытных данных. Наблюдается сильное расхождение (до 400 %) опытных данных с расчетом (рис. 5.20)

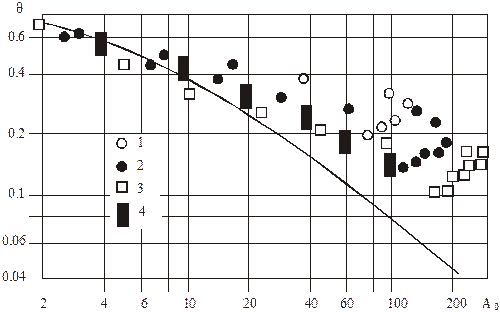
Рис. 5.20. Обработка опытов с использованием локальных значений

плотности и скорости

Таким образом, в градиентных потоках эффективность завесы определяется не только начальными или текущими значениями параметров потока, но и всей предысторией. Эту предысторию можно учесть, если использовать интегральные соотношения пограничного слоя. Формула (5.95) учитывает совместное влияние на  параметра , сжимаемости, градиента скорости.