Заметим, что если размерность Ф(/) есть, например [руб./год], а показателя //(ф) (Q —{py6.j, то размерность коэффициента рф равна [1/год.] Будем в дальнейшем полагать, что наличные фонды используются с полной (расчетной) загрузкой. Тогда рф =1 ис учетом указанных формальных соотношений между размерностями
На рис. 7.4 показана схема взаимосвязей показателей одномерного процесса расширенного воспроизводства валового продукта и его распределения на материально-вещественные компоненты (ср. с рис. 3.3 и 3.5). Здесь, как и на рис. 6.6, ПФ — блок одномерного преобразователя, описываемый производственной функцией, БР — блок распределения, описываемый соотношением динамического баланса
![]()
При сравнении (7.19) с (6.17) следует иметь в виду, что здесь предполагается Gp==0, поэтому G(t) +C(t} = V(f). Такое / предположение, характерное для моделирования экономического роста, означает, что в этой модели не учитывается ре новация основных производственных фондов, которые, будучи созданными, как бы не выбывают из производства и функционируют неограниченное время- Если не оговаривается иное, мы также примем это допущение, существенно упрощающее анализ процессов экономического роста.
Прирост интенсивности валового продукта по линейно-однородной ПФ согласно (7.11) и (7.16) определяется так:
![]()
или, учитывая (7.19),
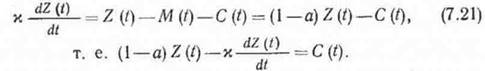
Заметим, что в данном случае факторы M{t} и G(t) балансовых уравнений не взаимозаменяемы в силу свойств линейно-однородной функции. Поэтому прирост интенсивности выпуска валового продукта (ср. с (6.20)) составит
![]()
Как и ранее, будем предполагать, что определяющим фактором роста является увеличение запаса основных производственных фондов, осуществляемое за счет капитальных вложений. Остальные ресурсы вовлекаются в производственный процесс в качестве обеспечивающих факторов с интенсивностями, зависящими от роста Ф(0. Тогда
![]()
Как показывают наблюдения, в динамике значение коэффициента связи между приростами выпуска продукта и капитальными вложениями, т. е. коэффициента приростной фондоемкости, отличается от статической нормы фондоемкости f, соответственно различаются коэффициенты приростной и общей фондоотдачи х = х~1 и / •--= f~ .
Одномерная зависимость между ростом валового продукта и чистыми капитальными вложениями (7.20) или (7.23) используется для анализа процесса воспроизводства в предположении отсутствия запаздываний в их реализации. При этой предпосылке коэффициент к характеризует инерционность экономической системы. Его размерность—[время], поскольку размерность Z(/), например, в стоимостном выражении равна (руб./время2], а капитальных вложений G{t)—[руб./время]. И если к равен, например, 1,4 года, это означает, что чистые капитальные вложения интенсивностью 1,4 [руб./год] обеспечивают за год прирост интенсивности валового выпуска на 1 (руб./год].
Зависимость, аналогичная (7.20), может быть получена для показателя прироста конечного продукта V. Так как Z(f)=
175
7i2i ^aV(f) (ср. с (6.31)), то коэффициент полной капиталоемкости
конечного продукта
![]()
v •-'--»/
Этот коэффициент показывает, каковы должны быть дополнительные капитальные вложения в народное хозяйство для получения единицы прироста конечного продукта. Соответственно}
![]()
Задавая связь между выпуском продукции и затратами факторов производства однородной ПФ, например для конечного продукта V(t}, в форме
![]()
Соотношение (7.26) характеризует влияние предельной эффективности Эф == —— основных производственных фондов, предельной производительности труда Э^ ==—— и технологической
д1^ dL „
структуры —— на изменение выпуска конечного продукта, обусловленное величиной ——• Полагая, что L зависит от Ф, запишем (7.26) в виде
![]()
Здесь функция <р характеризует изменяющуюся во времени эффективность использования капитальных вложений и по существу аналогична коэффициенту полной капиталоотдачи \1к(1}. Поэтому (7.27) можно представить как
![]()
Предполагая допустимость ее аппроксимации на рассматриваемом интервале времени некоторым средним значением, придем к соотношению (7.25).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.