Задачи по дисциплине "Теория обработки металлов давлением" (относительная деформация, зависимость нагрузки от удлинения материала), страница 3

35. А. Функция напряжения мембраны  для упругого кручения узкого прямоугольного бруса шириной  c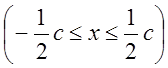задается .

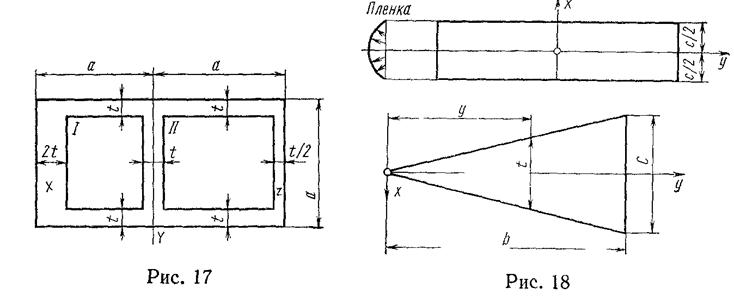
Используйте это выражение, выведите приближенную формулу для момента сопротивления кручению узкого треугольного сечения, показанного на рис.'18. Ь. Поясните кратко, как Вы используете песочную аналогию при пласти­ческом кручении нецилиндрических призматических брусьев. Найдите соотно­шение между крутящими моментами, необходимыми для создания пластических деформации во всем круглом и квадратном сечениях брусьев Площади сечений рaвны.

36. Турбина с внешним радиусом диска b, посажена на массивный вал ра­диуса а. Давление на внутреннюю поверхность считается постоянным, равным р. Если толщина диска у вала 2ha и сечение изменяется по гиперболе (рис. 19), то покажите, что пластические деформации появляются во всем сечении диска при  p= -Ya. Осевыми напряжениями в диске можно пренебречь.

37. А. Составной цилиндр с внутренним радиусом  и внешним  собран из п длинных цилиндров, все из одного и того же материала. Внутренний и внеш­ний радиусы каждого из цилиндров  Внутреннее давле­ние  равно (-р), внешнее  равно нулю (рис. 20) Покажите,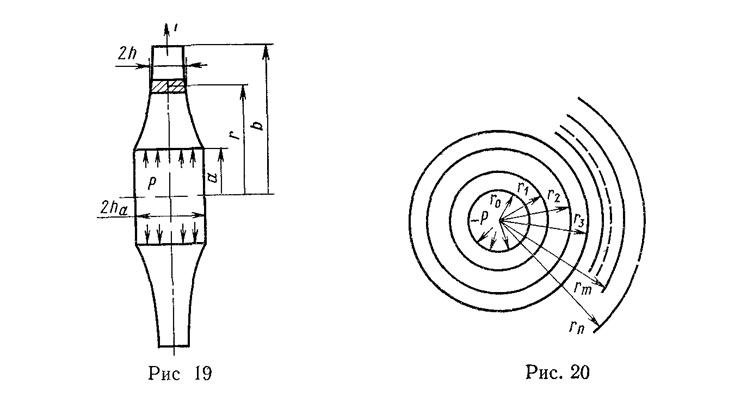

что в момент появления пластических деформаций одновременно на внутренних поверхностях всех цилиндров давление задается формулой

Если это давление становится максимальным, то покажите, что соотношение между внешним и внутренним радиусами каждого цилиндра равно  и

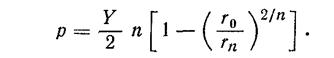
Сравните это значение р для различных значений и п стем, которое тре­буется, чтобы в таком же составном цилиндре все сечение было охвачено пласти­ческими деформациями. Используйте условие пластичности Треска и считайте, что изменения радиусов цилиндра не влияют на величину давления.

Б. Проделайте то же самое, когда n = 2, а напряжения текучести различны для двух разных материалов, т. е.Y1 и Y2.

38. Запаянный толстостенный цилиндр нагружен внутренним давлением р и одновременно крутящим моментом Т по всей его продольной оси. Если т - коэффициент диаметров, то найдите соотношения T/p, которые вызывают пласти­ческие деформации на внутренней и внешней поверхностях Используйте условие пластичности Мизеса.

39. Толстостенный цилиндр сделан из материала, для которого верхнее и нижнее значения напряжения пластического сдвига соответственно равны yu и yl. Покажите, что в частично пластическом состоянии внутреннее давление задается выражением.

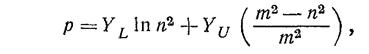
где т - коэффициент диаметров, п - соотношение между диаметром границы пластичности и диаметром отверстия. Каким будет выражение для толстостенной сферической оболочки из того же материала.

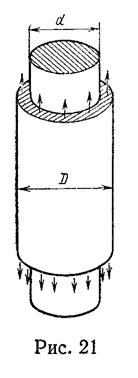
40. Тонкостенная трубка с постоянной толщиной стенки и внешним диа­метром D надета на массивный брус диаметром d (рис. 21). Найдите нагрузку, которую можно приложить к трубе прежде, чем произойдет потеря устойчивости. Предполагается, что трубка может скользить без трения по массивному брусу, к которому нагрузка не приложена. Для трубки 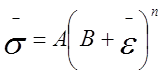. Обсудите эффект при наличии некоторого первоначального зазора  между трубкой и брусом.

41. Тонкое кольцо с начальным радиусом  = 75 мм вра­щается вокруг оси, проходящей через центр нормали к ее по­верхности Плотность материала  = 7840 кг/м³, и кривая упрочнения ее представлена выражением = 1400. Опре­делите угловую скорость, при которой произойдет потеря ус­тойчивости.

42. Сравните интенсивность деформации и деформации при потере устойчивости изотропного материала кривая упрочне­ния которого описана выражением 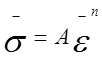 для следующих схем напряженного состояния.

А. Постоянное пропорциональное двухосное растяжение плоского листа.

Б. Круглая диафрагма, защемленная по контуру, нагружена с одной стороны давлением.

43. Проволоку протягивают через очко матрицы с пло­щадью поперечного сечения А, начальная площадь попереч­ного сечения проволоки А0. Волочение происходит, когда при­ложено заднее натяжение. Считают, что изменение формы происходит в результате однородной деформации. Докажите.

что напряжение волочения определяется выражением t == f+ Y In A0/A. Если наибольшая степень обжатия , которая может быть получена, составляет 50%, то чему равно заднее натяжение?

44. Длинная цилиндрическая заготовка радиусом а и длиной l окружена по цилиндрической поверхности инструментом, который может перемещаться по радиусу к оси заготовки и вызывать осевое выдавливание заготовки на двух концах. Коэффициент трения между заготовкой и инструментом . Найдите вы­ражения для изменения радиального давления и расстояния вдоль бруса. Четко сформулируйте ваши предположения.

Для заданного  и некоторого значения l/а выражение, которое Вы получили, можно изменить. Почему? Покажите, что это изменение должно иметь место, если напряжение полезного сдвига бруса k, когда

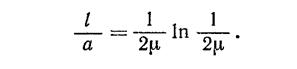
45. На рис. 22, а показано выдавливание материала через отверстие в ре­зультате перемещения трех ползунов. Сетка линий скольжения (с. л. с.) и годо­граф, приведенные на рис. 22, б, являются общим решением для комбинирован­ного и бокового выдавливания. Два ползуна  и RL движутся в противополож­ных направлениях с равными скоростями и , пока ползун rh движется пер­пендикулярно отверстию со скоростью и, сетка линий скольжения нарисована без учета трения на контактной поверхности между заготовкой и ползунами.

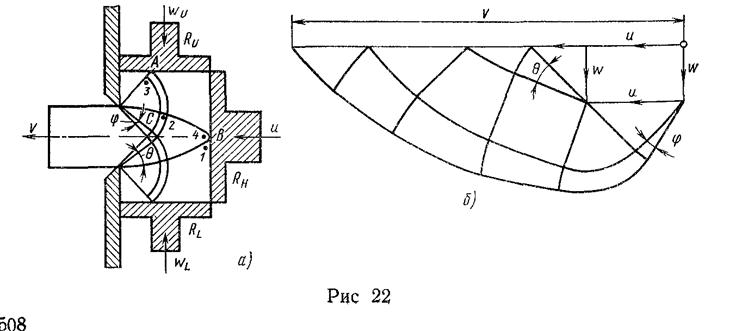
        А. При отсутствии трения в рассматриваемом выше случае под каким углом линии скольжения пересекают поверхность ползунов? Если трение сдвига пре­валирует на поверхности ползуна для  и rl, покажите как изменится с. л. с.

Б. Отметьте на с. л. с. линии  и . С учетом  (показаны на с. л. с.) и k найдите давления на ползун в точках А и В, ясно показывая, как Вы их определяете.

В. На годографе покажите векторы скоростей в точках 1, 2, 3 и 4 для за-данной  с. л. с.

Г. Покажите на годографе, нарисовав его заново, как он изменится для за­данной  с. л. с., если и  и = 0.

46. На рис. 23 показано волочение через гладкое очко матрицы с полууглом 20° для плоской деформации со степенью обжатия 0,19. Упрощенная с. л. с.

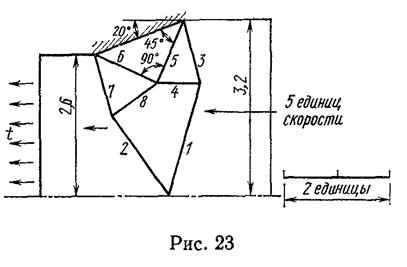
с границами разрыва скоростей также показана на рисунке. По­стройте годограф и вычислите верхнюю оценку напряжения во­лочения.

47. Куноги описал способ, по которому   толстостенные  трубы можно изготовлять, используя не­подвижный гладкий пуансон с боль­шим углом  при вершине конуса, вокруг которого данный кусок ме­талла вынужден расширяться при выдавливании через коническую матрицу в результате его сжатия между пуансоном и ползуном.

Обычно заготовка выдавливается ползуном того же диаметра, что и пуансон. Метод станет яснее при рассмотрении схемы на рис. 24, а. Обычные значения  и - от 10° до 30°. Характер линий разрывов скоростей для анали-зирования в условиях плоской деформации этого способа показан штриховой ли­нией на рисунке, где  единиц измерения. Нарисуйте соответствующий годограф и определите давления ползуна для задан­ной конфигурации. Пусть пуансон занимает различные положения справа и слева от заданного. Вычислите давление в каждом положении и покажите, что можно

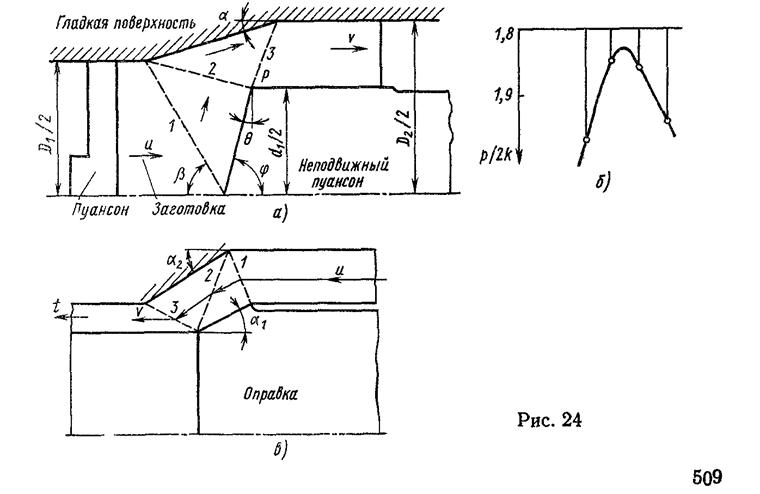
допустить такое положение пуансона, при котором будет минимальное давление на ползуне Куноги (Новый метод холодного выдавливания, 1956 г) выполнил обширные серии экспериментов, и выбранная им лучшая позиция пуансона по­хожа на показанную здесь.

48. Измените рис, 24, чтобы рассматривать случай, который требует постро­ения нескольких треугольников скорости на поверхности пуансона.