Задачи по дисциплине "Теория обработки металлов давлением" (относительная деформация, зависимость нагрузки от удлинения материала), страница 2

Так как одно главное напряжение должно быть растягивающим, укажите эту область на эллипсе, выражающем условие пластичности Мизеса для плоского напряженного состояния.

Какое максимальное значение напряжения может быть при двухосном напря­женном состоянии?

Нарисуйте графики, покажите, как нормальное напряжение изменяется в зависимости от максимального касательного напряжения?

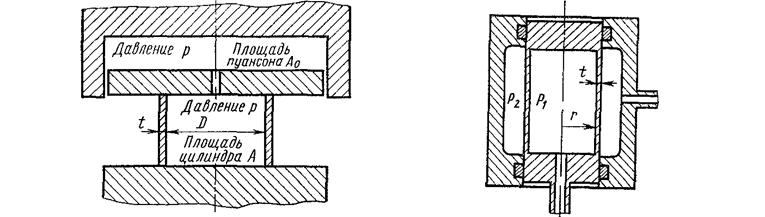
Рис. 10                             Рис. 11

20. На рис. 11 показан замкнутый тонкостенный круглый цилиндр с толщи­ной стенки t и радиусом r, установленный внутри другого цилиндра. Внутри тонко­стенного цилиндра создается давление , которое меньше давления , являющегося для него внешним.

о

Т1

Подшипники между внутренним и внешним цилин­драми обеспечивают свободное перемещение относительно оси.

Докажите, что если во внутреннем цилиндре появились пластические де­формации, соответствующие пределу текучести Y при одноосном растяжении, то  по условию пластичности Мизеса определяется выражением

где . Радиальными напряжениями и деформациями в сечениях, располо­женных вблизи днищ, можно пренебречь.

21. Длинная с запаянными концами тонкостенная трубка, текущий средний радиус которой r и средняя толщина стенки t, нагружена внутренним давлением р так, что она пластически деформируется. Материал трубки обладает ортотропной анизотропией, симметричной относительно нормали к поверхности трубки. В ре­зультате испытаний на растяжение установлено, что в плоскости пластичности r= 2.

Определите отношения окружной (тангенциальной), продольной деформа­ций и деформации по толщине. Сравните результаты с деформациями в изотропном теле. Упругими Деформациями можно пренебречь.

22. Низкий цилиндр с внутренним радиусом а и внешним b сжимается между параллельными плитами. Коэффициент трения между ними и материалом . Постройте эпюру распределения напряжения по толщине стенки цилиндра, пред­полагая, что  .

23. На рис. 12 показано сечение контейнера, в котором установлен кон­центрический, полый короткий и толстый цилиндр. С каждой стороны цилиндра находятся мягкие прокладки. Найдите выражение для  в переменных Y вдоль радиуса соприкосновения прокладки и цилиндра при появлении пластических деформаций. Коэффициент трения между цилиндром и прокладкой  , .

Контейнер считается жестким. Определите нормальное давление на стенку контейнера? Чему равно соотношение между , а, b и h, когда материал, сопри­касающийся с прокладкой, начинает сдвигаться при радиусе b? Рассмотрите его надежность (h-высота цилиндра).

24. Рассмотрите плоскую деформацию сжатия полосы металла высотой h, шириной 2а между двумя параллельными плитами. Коэффициент трения между металлом и плитами . Найдите выражение для определения среднего давления плит, необходимого для пластического течения;  считается малым. Если на­пряжение трения ( достигает значения напряжения текучести сдвига, получите выражение, учитывающее это. Нарисуйте график зависимости давления на по­верхности a при = const, если 2a/h = 7.

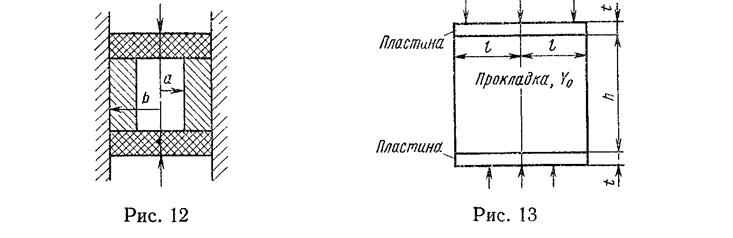
25. На рис. 13 показаны две тонкие параллельные плиты или прокладки толщиной t, узкие концы которых перпендикулярны плоскости рисунка. Мате­риал достаточно жесткий, но разрушается при растяжении, когда одноосные на­пряжения в нем достигают Y1. Зажатый между плитами материал неупрочнён, напряжение текучести сжатия для него Y0, толщина h. Материал заполняет все пространство между плитами, а при сжатии без трения может пластически растекаться в стороны. Сила сцепления на границе раздела всюду одинакова и равна напряжению текучести сдвига Y0/2. Покажите (приблизительно), что максималь­ная нагрузка сжатия, которую может выдержать заготовка между тонкими пли­тами, в [1 + (Y1lY0)(tlh)} раз больше той предельной нагрузки, которую она мо­жет выдержать без плит. Докажите, что благодаря тонким пластинам способность заготовки выдерживать нагрузку увеличивается на 30%, если Y = 3Y0 и t/h  = 1/10.

26. На рис. 14 показаны два широких листа из различных материалов. Для материала 1 напряжение текучести при одноосном растяжении Y1, и для мате­риала 2 - Y2. Листы обладают начальной кривизной и, пока не приложен изги­бающий момент М, свободны от напряжений. Оба листа сварены по границе раздела радиуса с. Найдите выражение для изгибающего момента Мр, действу­ющего на единицу ширины и вызывающего во всем слое металла пластическое течение. Тангенциальные напряжения в листе 1 растягивающие, а в листе 2 - сжимающие. Каким должно быть соотношение между а, b, с? Предполагается плоская деформация изгиба. Чему равен скачок тангенциальных напряжений при r = с? Убедитесь, что на поверхностях листа нет результирующих сил, а так же  проверьте свои ответы, считая Y1 = Y2.

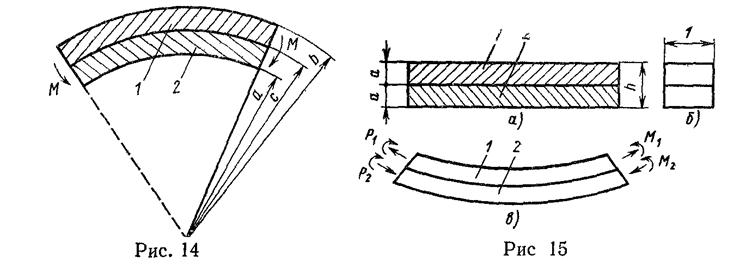
27. Узкая полоса состоит из двух металлических частей 1 и 2 одинаковой толщины, приваренных друг к другу (рис. 15). При температуре  они прямые, при повышении до температуры t полоса изгибается. Найдите радиус кривизны биметаллической полосы, считая деформацию упругой, а затем убедитесь, что наибольшее напряжение в каждой полосе будет на границе раздела. Чему равно изменение температуры, если пластическое течение начинается в двух металлах одновременно.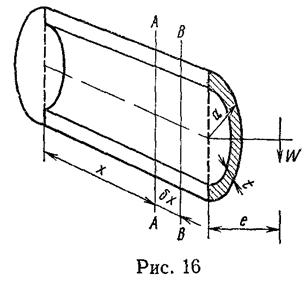                                            

28. На рис 16 изображен кронштейн с полукруглым сечением однородной тол­щины, на конце которого приложена на­грузка W. Обсудите, как можно найти при­ближенное выражение для определения рас­стояния между центрами сдвига' и круга с помощью зависимости напряжение - де­формация .

29. Рассмотрите изгиб широкого прямого бруса с прямоугольным поперечным сечением, к концам которого приложен изгибающий момент, вызывающий изгиб с кривизной 1/R. Предполагаем соотношение напряжение - относительная деформация .  Тогда уравнения, связывающие , М, R, даются выражением (7.3). Сравните радиальные напряжения, получаемые этим методом, и результаты, приведенные в подразделе 7. 2.

30. Балка АВ жестко защемлена по сечению В и поддерживается по сече­нию A, так что АВ горизонтальна. В промежуточном сечении С на расстоянии а oт A прикладывается направленная вниз нагрузка W. Полная длина кронштейна L. Найдите сечение приложения минимальной нагрузки W, соответствующее предельной несущей способности балки.                     

        31. Жесткая балка с круглым сечением радиусом r и длиной l жестко защем­лена в одном из концов и скручивается вокруг своей оси с угловой скоростью . Пусть зависимость между напряжением сдвига  и скоростью деформации сдвига такова: , где k, m - константы. Найдите необходимый крутящий момент.

        32. Полый шпиндель, отношение внутреннего радиуса которого к внешнему равно c, скручивается до тех пор, пока полностью не становится пластическим тогда крутящий момент снимают. Покажите, что остаточные касательные напряжения ост на внешнем радиусе равны k/3 при с = 0. Найдите положение радиуса при котором остаточные касательные напряжения равны нулю при с=0 и при с=1/2.                                                              

33. Полый шпиндель (с = 1/2) скручивается до тех пор, пока не становится пластическим на радиусе За/4 (см. подраздел 8 3). Постройте диаграмму распре­деления остаточных касательных напряжений по толщине стенки и в наиболее интересных точках. Укажите их значения. Какая часть первоначального угла скручивания остается после разгрузки?

34. Вычислите передаваемый крутящий момент и угол скручивания на еди­ницу длины для бруса, поперечное сечение которого и размеры указаны на рис 17 (а = 10 дюймов, t = 1 дюйм), если максимальное касательное напряжение сдвига не превышает 5000 фунтс/дюйм², G = 12-10⁶ фунтс/дюйм².