Разработка индивидуального электромеханического привода (мощность выходного вала привода - 1520 Вт, частота вращения выходного вала - 22 об/мин), страница 3

s_H=Z_H∙Z_M∙Z_e∙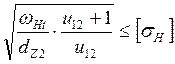, где   [s_H] - допускаемое контактное напряжение (см. п. 2.1.2);

Z_H - коэффициент, учитывающий форму сопряженных поверхностей, при x_å=0  Z_H = 1,77∙cosb = 1,77;

Z_M - коэффициент, учитывающий механические свойства материалов; для стальных колес Z_M= 275 (МПа);

Z_e -коэффициент,  учитывающий суммарную длину контактных линий;

w_Ht- удельная расчетная окружная сила.

Для прямозубых передач коэффициент, учитывающий суммарную длину контактных линий, равен

Z_e=, где   e_a - коэффициент торцового перекрытия.

e_a=, где    a_a - угол профиля зуба в точке на окружности вершин a_a ;

a_t1= a _w= a20°.

a_a=arccos, где d_Z и d_a  см. п. 2.1.3

a_a1=arccos,

a_a1=arccos.

Коэффициент торцового перекрытия

e_a==1,7.

Коэффициент, учитывающий суммарную длину контактных линий

Z_e=

Удельная расчетная окружная сила

w_Ht=

где     К_На - коэффициент, учитывающий распределение нагрузки между зубьями (для прямозубых передач К_На= 1);

К_Нb - коэффициент, учитывающий неравномерность распределения нагрузки по ширине винца (К_Нb= 1,05);

K_Hv - коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении;

K_Hv=1+, где  w_Hv - удельная окружная динамическая сила (w_Hv= 7,96 Н/мм).

 K_Hv=1+.

Удельная расчетная окружная сила

w_Ht= Н/мм.

Контактное напряжение

s_H =1,77∙275∙0,876∙=230<413,7 МПа.

Проверочный расчет зубьев на выносливость по напряжениям от изгиба

s_F= Y_F∙Y_e∙Y_b∙, где   Y_F - коэффициент (для шестерни Y_F =3,9, для колеса Y_F=3,6);

w_Ht-удельная расчетная окружная сила;

Y_b - коэффициент, учитывающий наклон зуба, (для прямозубых передач Y_b=1);  m_n- модуль ширины зубчатых колес (для шестерни m_n=1,07 мм, для колеса m_n=1,345 мм);

Y_e - коэффициент, учитывающий перекрытие зубьев;

Y_e=, где K_e - коэффициент среднего изменения суммарной длинны контактных линий (для обоих колес K_e= 0,95)

e_a-коэффициент торцового перекрытия (e_a=1,7)

Коэффициент, учитывающий перекрытие зубьев

Y_ε==0,62.

Удельная расчетная окружная сила

ω_Ft=, где K_Fα     - коэффициент, учитывающий распределение нагрузки между зубьями (для прямозубых передач К_Fα= 1);

K_Fβ- коэффициент, учитывающий неравномерность распределения нагрузки по ширине винца (K_Fβ= 1,17);

K_Fγ - коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении;

K_Fγ=1+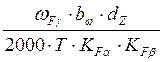, где     ω_Fγ - удельная окружная динамическая сила (ω_Fγ=21,22 Н/мм);

для шестерни K_Fγ= 1+, для колеса K_Fγ= 1+.

Удельная расчетная окружная сила для шестерни ω_Ft== 42,35 Н/мм; для колеса ω_Ft== 41,7 Н/мм.

Выносливость по напряжениям от изгиба для шестерни          σ_F=3,9∙0,62∙1∙=74,5 < 129,6 МПа;

для колеса σ_F=3,6∙0,62∙1∙=67,7 < 124,8 МПа.

Проверочный расчет зубьев на кратковременную перегрузку.

σ_Hmax=σ_H∙[σ_Hmax], где T_пик=2∙T

[σ_Hmax] - предельно допустимое контактное напряжение;

σ_H-контактное напряжение (σ_H= 230 МПа);

σ_Hmax=230∙=325,27 < 1960 МПа;

σ_Fmax=σ_F∙ [σ_Fmax], где Т_пик=2∙T

[σ_Fmax] - предельно допустимое изгибное напряжение;

σ_F - изгибное  напряжение  (для  шестерни σ_F =74,5 МПа, для колеса σ_F = =67,7 МПа);

для шестерни σ_Fmax = 74,5∙2 = 149 < 560 МПа;

для колеса σ_Fmax = 67,7∙2 = 135,4 < 560 МПа;

2.1.5 Расчет открытых передач

Аналогично расчетам п. 2.1.5 рассчитываем открытые передачи. Ориентировочное значение делительного межосевого расстояния

a₂=K_a∙(u₃₄+1)∙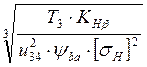, где T₃ - исходная расчетная нагрузка (T₃=146,92 H∙м);

u₃₄ - передаточное число (u₃₄= 6,31);

а₂ = 140мм.

Определяем модуль колес Z₃ и Z₄

m₂=мм.

По СТ СЭВ 310-76 принимаем т₂= 1,5 мм.

Делительные диаметры колесZ₃' и Z₄

 d_z3 =39 мм, d_Z4=246 мм.

Диаметр вершин зубьев колес Z₃ и Z₄

d_a3=42 мм; d_а4= 249 мм.

Диаметр впадин колес Z₃ и Z₄

d_f3 = З5,З мм; d_f4 = 242,3 мм.

Ширина зубчатых венцов колес Z₃ и Z₄

b_ω2=ψ_ba∙a₂=56мм.

Ориентировочное значение делительного межосевого расстояния а₃ =K_a∙(u₃₄+1)∙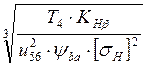, где T₄ - исходная расчетная нагрузка (T₄ =793,04 Н∙мм);