Пояснительная записка на курсовую работу "Балочная клетка из стали", страница 7

s_пр=Ös₁²+s_у²-s₁•s_у+3•t_ху²£1.15•R_y•g_c ,                  (7.1)

где s₁ – нормальные напряжения общего изгиба в верхней части стенки (смотреть рис. 8.1), определяемые по формуле [3]

s₁=s_1max•h_w/h, кН/см²                                               (7.2)

где s_1max – максимальное напряжение в месте изменения сечения, кН/см²;

s_у=0 – местные напряжения;

R_у=38 кН/см² – расчетное сопротивление;

g_с=1 – коэффициент условия работы;

t_ху – средние касательные напряжения в сечении, определяемые по формуле [3]

t_ху=Q₁/(t_w•h_w)=q_гб•(L/2-x)/( t_w•h_w), кН/см²              (7.3)

где q_гб – расчетная погонная  нагрузка на главную балку, кН/м.

Максимальные касательные напряжения действуют на опоре. Их величина определяется по формуле [3]

t_max=Q_гб•s₁/(I₁•t_w)£R_s•g_c=0.58•R_y•g_c ,                       (7.4)

где Q_гб – максимальная расчетная поперечная сила действующая на главную балку, кН;

I₁ – момент инерции уменьшенного сечения, см⁴;

t_w - толщина стенки, см;

s₁ – статический момент отсеченной половины сечения относительно нейтральной оси, определяемый по формуле [3]

s₁=b₁•t•(h-t)/2+t_w•h_w²/8, см³                                       (7.5)

где b₁ – ширина пояса в месте изменения сечения, см;

t – толщина полки, см;

h – высота балки, см;

h_w - высота стенки, см.

По формулам (7.2), (7.3), (7.1) проверяем прочность по приведенным   напряжениям:

s₁=30.49•166.4/170=29.84 кН/см²;

t_ху=315.62•(12.6/2-2.1)/(1.2•166.4)=6.64 кН/см²;

s_пр=Ös₁²+3•t_ху²=Ö29.84²+3•6.64²=31.94 кН/см²<1.15•38•1=43.7 кН/см².

Прочность по приведенным напряжениям в сечении 1 – 1 обеспечена.

По формулам (7.5), (7.4) проверяем прочность по максимальным касательным напряжениям:

s₁=20•1.8•(170-1.8)/2+1.2•166.4²/8=6171.744 см³;

t_max=1988.4•6171.744 /(969986.6•1.2)=

=12.26кН/см²=122.6 МПа<0.58•380•1=220.4 МПа.

Прочность по максимальным касательным напряжениям обеспечена.

Поверку жесткости следует проводить при h£ h_min  по формуле

f / l £ [f / l]

f / l= q_гб•l³/Е•(1/81•Е•I+1/1481•Е•I)=

=315/62•1260³ • (1\81•14228304•2.06•10⁴+

+1/1481•969986.6•2.06•10⁴) /2.06•10⁴=0.000014£ [f / l]=1/400=0.0025

Жесткость балки обеспечена.

Проверка общей устойчивости балки производится по формуле [3]

s=М_гб/(j_б•W)£R_y•g_c ,                                      (7.6)

где j_б определяется по [1].

Общую устойчивость по формуле (7.6) можно не проверять, если балка по всей длине закреплена настилом, а при его отсутствии выполняется неравенство [3]

l_ef/b<[l_ef/b]=[0.41+0.0032•b/t+(0.73-0.016•b/t) •b/h] •ÖE/R_y ,      (7.7)

где l_ef – расстояние между точками закрепления балки из плоскости, см;

b – ширина пояса главной балки, см;

t – толщина пояса, см;

h – высота главной балки, см;

Е – модуль упругости, кН/см²;

R_y – расчетное сопротивление, кН/см².

По формуле (7.7) определяем

210/38=5.526<[0.41+0.0032•38/1.8+

+(0.73-0.016•38/1.8) •38/170] •Ö(2.06•10⁴)/38=13.16

Общая устойчивость балки обеспечена.

8. Проверка устойчивости пояса и стенки балки

Устойчивость пояса считается обеспеченной [3], если

b_ef/t£0.5•ÖE/R_y,

где b_ef – свес пояса.

В данном случае это неравенство реализовано в разделе 5.4.

Для проверки устойчивости стенки, первоначально определяем необходимость постановки ребер жесткости согласно [3] по формуле

l_w=h_w/t_w•ÖR_y/E,                                (8.1)

где l_w - условная гибкость стенки;          

l_w=166.4/1.2•Ö38/2.06•10⁴=5.95>3.5,

что говорит о необходимости проверки устойчивости стенки и необходимости постановки поперечных ребер жесткости. Предельное расстояние между ребрами 2•h_w=2•166.4=332.8 см. Принимаем симметричные двухсторонние ребра жесткости с шагом, равным шагу вспомогательных балок рис. 8.1.

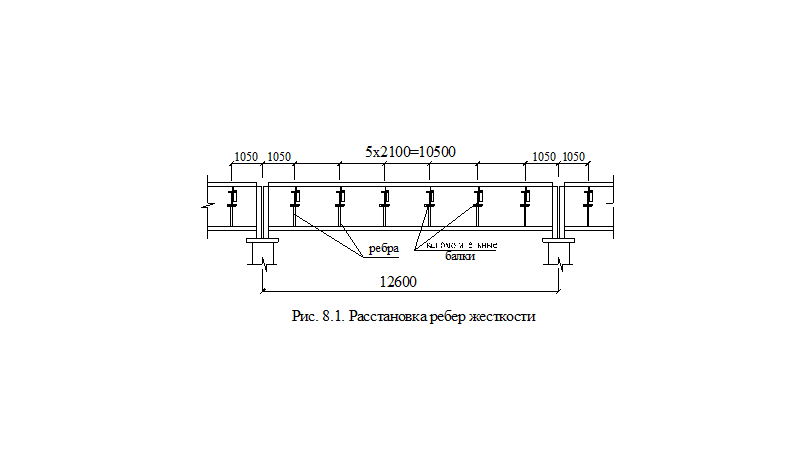
Расчет на устойчивость каждого отсека балки при отсутствии местных напряжений и l_w<6 следует выполнять по формуле согласно [3]

Ö(s/s_cr)²+(t/t_cr)²£g_c,                            (8.2)