Пояснительная записка на курсовую работу "Балочная клетка из стали", страница 12

k_f=0.15•N/(l_w•b_f•R_wf•g_wf•g_c)=0.15•3366•10/0.7•215•267•1•1=0.125 см,

по металлу границы сплавления

k_f=0.15•N/(l_w•b_z•R_wz•g_wz•g_c)=0.15•3366•10/1•267•0.45•470•0.85•1=0.105 см.

Принимаем катет шва k_f=6 мм по [1, п.п. 12.8б, табл. 38].

15. Расчет оголовка колонны

Сопряжение балок с колоннами свободное (шарнирное). Свободное сопряжение передает только вертикальные нагрузки. При свободном сопряжении балки обычно ставят на колонну сверху, что обеспечивает простоту монтажа. В нашем случае опирание балок сверху. В этом случае оголовок колонны состоит из плиты  и ребер, поддерживающих плиту и передающих нагрузку на стержень колонны (рис. 15.1).

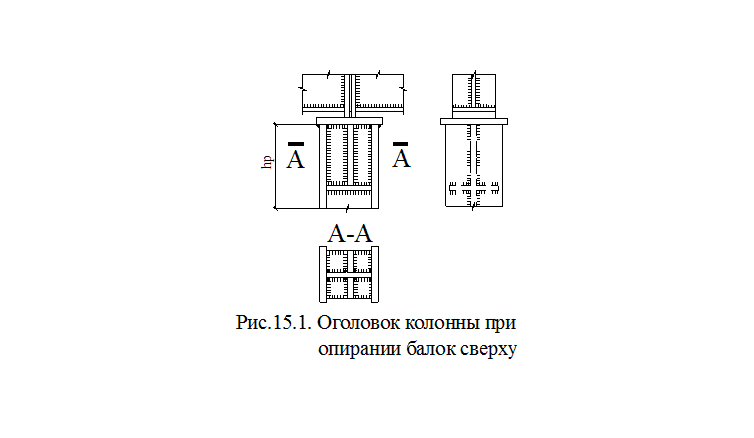
     Нагрузка передается на колонну через фрезерованные торцы опорных ребер балок, расположенных близко к центру колонны, следовательно, плита оголовка поддерживается снизу ребрами, идущими под опорными ребрами балок. Ребра оголовка привариваются к опорной плите и к ветвям колонны при сквозном  стержне. Швы, прикрепляющие ребро оголовка к плите, должны выдерживать полное давление на оголовок.

Примем k_ш=9мм

δ=N/(Sl_w•k_ш)£b_f•R_wf•g_wf•g_c  

δ=3366/0.9•267=14кН/см²)£0.7•21.5•1•1=15.05  

Толщину опорной плиты принимаем конструктивно d_пл=24 мм.

Толщину ребра оголовка определяем из условия сопротивления на смятие под полным опорным давлением, согласно [2]

t_р=N/(l_см•R_p),                  (16.1)

где N=Q_гб=3366 кН;

l_см=68 см – длина сминаемой поверхности, равная ширине опорного ребра балки плюс две толщины плиты оголовка колонны;

R_р – расчетное сопротивление стали смятию торцевой поверхности;

R_p=R_un/g_m=47/1.025=45.8 кН/см².

По формуле (16.1) определяем

t_p=3366/(68•45.8)=1.08 см.

Принимаем t_p=12мм.

Высоту ребра оголовка определяем, требуемой длиной швов, передающих нагрузку на стержень колонны. Длина швов не должна быть больше 85•b_f•k_f.

h_p=N/(4•k_ш•b_f•g_wf•R_wf•g_c)=3366/(4•0.9•0.7•1•21.5•1)=62.12 см.

Принимаем h_p=64 см.

Толщину ребра проверяем на срез по формуле согласно [2]

t=0.5•N/(2•h_p•t_p)= 0.5•3366/(2•64•1.2)=10.95 кН/см²£

£R_s=0.58•R_yn/g_m=0.58•32.5/1.025=18.4 кН/см².

Расстояние между ветвями сквозной колонны определим из условия равноустойчивости колонны относительно свободной и материальной осей, т. е. l_х=l_ef. Рассчитаем соединение ветвей планками.

Для стержней сквозного сечения с планками l_ef определяется по

[1, табл.7]. Предельно допустимая гибкость ветви на участке между планками должна быть не более 40. Следовательно, расстояние между планками в свету можно найти из условия [5]

l₁=l_в/i_y;             l_в/2.79=40;         тогда l_в^max =112 см.

Примем расстояние между планками в свету l_в=100 см. Тогда гибкость ветви между планками будет равна

l₁=l_в/i_y=100/2.79=35.84, что меньше предельно допустимой по [1, п.5.6].

Если принять, что по [1, табл.7]

l_ef=Öl_y²+l₁², тогда

l_y=Öl_ef²-l₁²=Öl_x²+l₁²=Ö65.9²-35.84²=55.3.

Расстояние между ветвями колонны b₀ можно определить по формуле согласно [5]

b₀=l_ef,y/(a₂•l_y)=890/(0.52•55.3)=31 см,

где коэффициент a₂ принят согласно [5, табл.2].

Расстояние между полками двутавров в свету равно

b₁=b₀-b_п=31-14=17 см.

Принимаем размеры планки, приведенные на рис.15.3.

b_пл=b₁+6 см=23 см;

d_пл=(0.5…0.75)b₀=15.5…23.25 см. Принимаем d_пл=20 см.

Толщина планки берется из конструктивных соображений t_пл=1 см.

Определим соотношение I_s•l, где

I_в•b

I_s – момент инерции сечения планки относительно оси Х – Х;

l=120 см  – расстояние между центрами планок;

b=b₀=31 см – расстояние между осями ветвей;

I_в=419 см⁴ – момент инерции сечения ветви относительно оси 1 – 1.

I_s=t_пл•d_пл³/12=1•20³/12=666.7 см⁴,

I_s•l/(I_в•b)=666.7•120/(419•31)=6.2>5, следовательно, формула для l_ef принятая по [1, табл.7] верно.

Вычислим момент инерции сечения колонны относительно свободной оси У –У (рис. 15.2).

I_y=2•(I_в+А_в•b₀²/4)=2•(419+53.8•31²/4)=26688.9 см⁴;

i_y=ÖI_y/(2•A_в)=Ö26688.9/(2•53.8)=15.75 см;