Записывая
ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы,
отвечающие утверждениям, которые вы считаете неправильными. Например,
если вы считаете правильными утверждения А и В, а неправильными — утверждения Б
и Г, запишите ![]()
![]()
![]()
![]() . Если хотя бы одна буква из 4-х будет не
отмечена, задание считается невыполненным.
. Если хотя бы одна буква из 4-х будет не
отмечена, задание считается невыполненным.
|
1. Дан куб ABCDA1B1C1D1. Выберите правильное утверждение. –А. Прямая AB пересекается с плоскостью DCC1. –Б. Прямая AB и плоскость B1C1D1 имеют общие точки. +В. Прямая AB параллельна плоскости, которая проходит через прямые DC и A1B1. –Г. Прямая AB параллельна плоскости B1C1C. |
|
2. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Выберите правильное утверждение.
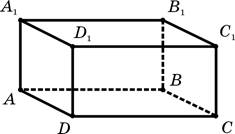
–А. Плоскости ABC и A1B1C1 пересекаются.
–Б. Плоскости ABC и DCC1 не имеют общих точек.
+В. Плоскости ABB1 и DCC1 параллельны.
–Г. Плоскости ADD1 и BCC1 имеют общие точки.
|
3. Отрезок A1B1 — параллельная проекция отрезка AB на плоскость a. Точка C лежит на отрезке AB. Выберите правильное утверждение. –А. Проекция точки C на плоскость a не принадлежит отрезку A1B1. –Б. Отрезки AB и A1B1 не лежат в одной плоскости. |
|
+В. Если AC : BC = 2 : 3, то A1C1 : C1B1= 2 : 3.
–Г. Если AC = CB, то A1C1 = 2 C1B1.
4. Параллелограмм ABCD и треугольник ABS лежат в разных плоскостях, MN — средняя линия треугольника ABS. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
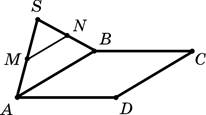
–А. Прямая MN пересекает плоскость ABC.
+Б. Прямая MN и плоскость ABC параллельны.
–В. Прямая BS параллельна плоскости ADC.
+Г. Прямая DC и плоскость ABS параллельны.
|
5. Точка O лежит между параллельными плоскостями a и b.Две прямые a и b, которые проходят через точку O, пересекают плоскость a в точках A1, B1, a плоскость b — в точках A2, B2. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. +А. Если A1B1 = A2B2, то обязательно A1B2 = B1A2. |
|
–Б. Прямые A1B1 и A2B2 скрещивающиеся.
+В. Прямые A1B1 и A2B2 параллельны.
+Г. Прямые a и b лежат в одной плоскости.
6. Четырехугольник A1B1C1D1 является параллельной проекцией трапеции ABCD (AD— основание трапеции) на некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Четырехугольник A1B1C1D1 является трапецией с основанием A1B1.
–Б. Четырехугольник A1B1C1D1 может быть параллелограммом.
+В. Четырехугольник A1B1C1D1 является трапецией с основанием B1C1.
+Г. Четырехугольник A1B1C1D1 является трапецией с основанием A1D1.
|
7. Дан треугольник ABC. Плоскость a, параллельна прямой AB, пересекает сторону AC в точке K, а сторону BC — в точке L. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. –А. Прямая KL пересекает прямую AB. +Б. Если AK = KC, то BL = LC. |
|
+В. Треугольники ABC и KLC подобны.
–Г. Если CL = LB, KL = 12 см, то AB > 24 см.
8. Даны две плоскости a и b, которые пересекаются. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Не существует прямой, которая параллельна как плоскости a, так и плоскости b.
–Б. Любая прямая, которая пересекает плоскость a, пересекает и плоскость b.
–В. Существует плоскость, которая параллельна как плоскости a, так и плоскости b.
–Г. Любая плоскость, которая пересекает плоскость a, пересекает также плоскость b.
9. Прямые a1 и b1 являются параллельными проекциями прямых a и bна некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Если прямые a1 и b1 параллельны, то обязательно прямые a и b тоже параллельны.
+Б. Если прямые a и b скрещивающиеся, то прямые a1 и b1 могут быть параллельными.
–В. Если прямые a1 и b1 пересекаются, то прямые a и b обязательно пересекаются.
–Г. Если прямые a и b не пересекаются, то прямые a1 и b1 обязательно не пересекаются.
|
10. Дан квадрат ABCD. Точка S равноудалена от каждой вершины квадрата, точки K, L, M — середины отрезков SA,SD,BC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. +А. Прямая KM параллельна плоскости SCD. –Б. Прямая LC пересекает плоскость SKM. +В. Четырехугольник KLCM — параллелограмм. +Г. Если SA = AD = 4 см, то KM > pсм. |
|
|
11. Три параллельные плоскости a, b, g пересекают скрещивающиеся прямые |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.