находить наибольшее и наименьшее значение функции на заданном промежутке;
¾ исследовать функции с помощью производной и строить графики функций.
Следует обратить внимание на то, что в заданиях этого теста используется понятие критической точки функции, которое необходимо для исследования функции. Критические точки — это внутренние точки области определения заданной функции, в которых производная равна нулю или не существует. Те внутренние точки области определения функции, в которых производная равна нулю, еще называют стационарными точками.
Также следует обратить внимание на то, что при исследовании функций на возрастание, убывание и экстремумы для получения соответствующих промежутков достаточно на области определения заданной функции отметить ее критические точки и разбить область определения на промежутки.
Вариант 1
Записывая ответы на задания теста,
обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и
зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными.
Например, если вы считаете правильными утверждения А и В, а
неправильными — утверждения Б и Г, запишите 
.
Если хотя бы одна буква из 4-х будет не
отмечена, задание считается невыполненным.
1. Известно, что 
= 2x
– 4.
Выберите правильное утверждение.
–А. Есть такие значения х, при которых производная функции х2 – 4х не существует.
–Б. Производная функции х2 – 4х ни при каких значениях х не равна нулю.
–В. Производная функции х2 – 4х равна нулю при х = –2.
+Г. Критической точкой для функции х2 – 4х является х = 2.
2. Известно, что производная некоторой функции f (x) имеет такие знаки, как на рисунке
Учитывая, что на тех промежутках, где производная положительна, функция f (x) возрастает, выберите правильное утверждение.
–А. Функция возрастает на промежутке (–¥; 2).
–Б. Функция возрастает на промежутке (3; +¥).
+В. Функция возрастает на промежутке (2; 3).
–Г. Нет такого промежутка, где заданная функция возрастает.
|
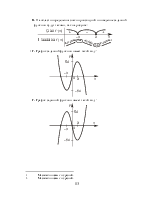
3. На рисунке изображен график некоторой функции y = f (x). Выберите правильное утверждение. –А. хо = – 2 — точка минимума. +Б. хо = 2 — точка максимума. –В. хо = 0 — точка минимума. –Г. хо = –1 — точка максимума. |
|
4. Задана функция f (x) = х3 – 27х. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. f¢(x) = 3х2 – 27.
–А. f¢(x) = 3х2 + 27.
+Б. f¢(x) существует при всех действительных значения х.
–Б. Есть такие значения х, при которых f¢(x) не существует.
+В. Производная функции f (x) равна нулю при х = 3 и при х = –3.
–В. Производная функции f (x) равна нулю только при одном значении х = 3.
+Г. Заданная функция имеет две критические точки: х = 3 и х = –3.
–Г. Заданная функция имеет только одну критическую точку: х = 3.
5. Функцию f (x) = х3 – 12х исследуют на возрастание и убывание. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. f¢(x) = 3х2 – 12.
–А. f¢(x) = х2 – 12.
+Б. f¢(x) = 0 при x = 2 и при x = –2.
–Б. f¢(x) = 0 только при одному значении х = 2.
+В. f¢ (x) > 0 на каждом из промежутков (–¥; –2) и (2; +¥).
–В. f¢ (x) > 0 на промежутке (–2; 2).
+Г. Функция возрастает на каждом из промежутков (–¥; –2) и (2; +¥)..
–Г. Функция возрастает на промежутке (–2; 2).
6. Известно, что производная функции f (x) = х3 – 3х имеет такие знаки, как на рисунке, и f¢(–1) = f¢(1) = 0
Учитывая, что максимум или минимум функция может иметь только в своих критических точках, отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. В точке минимума производная заданной функции меняет знак с “–” на “+” (при движении слева направо).
–А. В точке минимума производная заданной функции меняет знак с “+” на “–” (при движении слева направо).
+Б. Точка х = 1 является точкой минимума функции f (x).
–Б. Точка х = –1 является точкой минимума функции f (x).
+В. В точке максимума производная заданной функции меняет знак с “+” на “–” (при движении слева направо).
–В. В точке максимума производная заданной функции меняет знак с “–” на “+” (при движении слева направо).
+Г. Точка х = –1 является точкой максимума функции f (x).
–Г. Точка х = 1 является точкой максимума функции f (x).
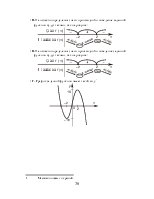
7. Задана функция f (x)
= 
. Отметьте, какие из
следующих четырех утверждений правильные, а какие — неправильные.
+А. Областью определения заданной функции является промежуток [0; 2].
–А. Областью определения заданной функции являются промежутки (–¥; –2] та [2; +¥).
+Б. f¢(x) = 
.
–Б. f¢(x) = 
.
+В. На
области определения заданной функции (в выделенных на рисунке интервалах) знаки производной будут такими, как на
рисунке
–В. На
области определения заданной функции (в выделенных на рисунке интервалах) знаки производной будут такими, как на
рисунке
+Г. Заданная функция возрастает на промежутке (0; 1) и убывает
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
