Показательная функция. Показательные уравнения и неравенства: Вариативные тестовые вопросы по алгебре (Варианты 1-4 по 12 вопросов с отметками правильных ответов)

Заданное неравенство и неравенство x – 2 > 2 имеют одинаковые решения.

+Г. Решением заданного неравенства является x < 4.

–А. График функции y = 3  имеет вид:	+Б. График функции y = 3  имеет вид:
–В. График функции y = 3  имеет вид:	+Г. Уравнение 3 =   не имеет решений.

+А. Заданное уравнение можно записать в виде: 4×2 – 9×2 + 2 = 0.

–Б. Если в заданном уравнении выполнить замену 2 = t, то получим уравнение 4t² + 9t + 2 = 0.

+В. Корни заданного уравнения совпадают с корнями хотя бы одного из уравнений 2 = 2 или 2 = .

–Г. Заданное уравнение имеет единственный корень.

+А. Заданное неравенство равносильно неравенству 5+ 3×5– 4 > 0.

–Б. Если в заданном неравенстве выполнить замену 5= t, то получим неравенство t² + t – 4 > 0.

+В. Заданное неравенство равносильно неравенству 5 > 1.

+Г. Решением заданного неравенства является x > 0.

+А. Если обе части заданного уравнения разделить на 5 ¹ 0, то получим уравнение, в котором правая часть будет числом.

–Б. Функция f(x) =  + является возрастающей функцией.

–В. Если функция f(x) убывающая (или возрастающая), то уравнение f(x) = 1 может иметь два корня.

+Г. Заданное уравнение имеет единственный корень x = 2.

–А. Заданное уравнение можно записать в виде: 3 – 7×3×5 = 8×5.

+Б. Если члены заданного уравнения записать как степени чисел 3 и 5, то сумма показателей степеней у любого из членов уравнения будет одинаковой и равной 2x.

+В. Если обе части заданного уравнения разделить на 5 ¹ 0, то получим равносильное уравнение  + 7× = 8.

+Г. Заданное уравнение равносильно уравнению  = 1.

+А. Заданная система равносильна системе

–Б. Если выполнить замену u = 2, v = 3, то получим систему  

+В. Заданная система равносильна системе

–Г. Заданная система имеет два решения.

Вариант 2

–А. Графиком заданной функции является прямая.

–Б.  Заданная функция убывает на всей области определения.

+В. График заданной функции имеет вид:

–Г. График заданной функции имеет вид:

–А. Правую часть заданного уравнения можно записать так: 4.

+Б. Заданное уравнение можно записать в виде: 4 = 4.

–В. Из заданного уравнения следует, что  x – 1 = – 3.

–Г. Заданное уравнение имеет корень, больший 6.

–А. Число 4 является решением заданного неравенства.

–Б. Из заданного неравенства следует, что  3x < 12.

+В. Из заданного неравенства следует, что  3x > 12.

–Г. Решением заданного неравенства является x < 4.

+А. В область определения заданной функции входят все действительные числа.

+Б. График заданной функции имеет вид:

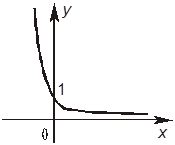
–В. Заданная функция возрастает на всей области определения.

–Г. Множество значений заданной функции — все действительные числа.

–А. Левую часть заданного уравнения можно записать так: 3 × 3

+Б. Заданное уравнение можно записать в виде: 3 = 3.

–В. Из заданного уравнения следует, что   + 2x = 2x – 1.

+Г. Корень заданного уравнения больше  (–2).

–А. Правую часть заданного неравенства можно записать так: .

–Б. Заданное неравенство можно записать в виде:  > .

+В. Заданное неравенство и неравенство x + 4 > 2 имеют одинаковые решения.

+Г. Решением заданного неравенства является x > –2.

+А. График функции y = 5  имеет вид:	–Б. График функции y = 5  имеет вид:
+В. График функции y = 5  имеет вид:	–Г. Уравнение 5 =  имеет только одно решение.

–А. Заданное уравнение можно записать в виде: 9×3 – 26×3 – 3 = 0.

+Б. Если в заданном уравнении выполнить замену 3 = t, то получим уравнение 9t² + 26t – 3 = 0.

+В. Все корни заданного уравнения совпадают с корнями уравнения