решать квадратные неравенства, пользуясь графиком соответствующей квадратичной функции;
¾ использовать квадратные неравенства при нахождении области определения выражений, которые содержат квадратные корни.
Вариант 1
Записывая ответы на
задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными,
и зачеркните буквы, отвечающие
утверждениям, которые вы считаете неправильными. Например, если вы считаете
правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите 
. Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.
1. Используя то, что графиком квадратичной функции y = ax2 + bx + c (a ¹ 0) является парабола, ветви которой направлены вверх при a > 0 и вниз при a < 0, выберите правильное утверждение.
–А. Графиком функции y = 2x2 + x является прямая.
–Б. Графиком функции y = 2x2 + x является парабола, ветви которой направлены вниз.
–В. Графиком функции y = –2x2 + x является парабола, ветви которой направлены вверх.
+Г. Графиком функции y = –2x2 + x является парабола, ветви которой направлены вниз.
2. Задана функция y = x2 – 6x + 3. Учитывая то, что для параболы —
графика функции y = ax2 + bx + c (a ¹ 0)
— координатой по оси x вершины параболы является xо = –
, выберите правильное утверждение.
–А. Для заданной функции соответствующие коэффициенты равны a = 1, b = 6.
–Б. Для заданной функции соответствующие коэффициенты равны a = 1, b = 3.
+В. xо = 3.
–Г. xо = –3.
|
3. Чтобы решить неравенство x2 – 2x – 3 > 0, построили график функции y = x2 – 2x – 3 (см. рисунок). Выберите правильное утверждение. –А. Заданная функция не принимает положительных значений ни при каких значениях x. –Б. Заданная функция принимает положительные значения при –1 < x < 3. |
|
+В. Заданная функция принимает положительные значения при x < –1 и при x > 3.
–Г. Заданная функция принимает положительные значения при x = –1 и x = 3.
4. Задана функция f (x) = –x2 + 3x – 2. Отметьте, какие из приведенных четырех утверждений о пересечении графика функции с осями координат правильные, а какие — неправильные.
+А. В точках пересечения графика заданной функции с осью y значение x = 0.
–Б. График функции f (x) пересекает ось y в точке (0; 2).
+В. В точках пересечения графика заданной функции с осью x значение f (x) = 0.
–Г. График заданной функции пересекает ось x при x = –1 и x = –2.
5. Чтобы решить квадратное неравенство –x2 + 2x > 0, нашли нули функции f (x) = –x2 + 2x и построили график функции f (x). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Чтобы найти нули функции f (x), надо решить уравнение x2 + 2x = 0.
–Б. Функция f (x) равна нулю при x = 1 и при x = –2.
+В. График функции y = –x2 + 2x имеет такой вид
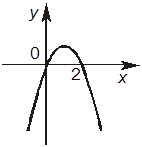
–Г. Решением заданного неравенства является промежуток (–¥; 0).
6. Для решения неравенства (x – 1)(x – 2) < 0 раскрыли скобки и получили квадратное неравенство x2 – 3x + 2 < 0. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Функция x2 – 3x + 2 равно нулю при x = –1 и при x = –2.
+Б. График функции y = x2 – 3x + 2
имеет такой вид
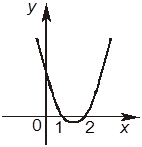
–В. Решением заданного неравенства являются промежуток (–¥; 1) и промежуток (2; +¥).
+Г. Решением заданного неравенства является промежуток (1; 2).
7. Задана функция y = x2 – 4x – 1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Абсцисса вершины параболы (графика заданной функции): xо = –2.
–Б. Ордината вершины параболы (графика заданной функции): yо = 5.
+В. График заданной функции
имеет такой вид:
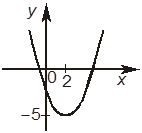
–Г. График заданной функции
имеет такой вид:
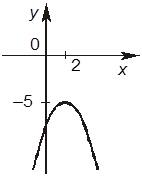
8. Задано неравенство x2 – 5x + 6 > 0. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. График f (x) = x2 – 5x + 6 пересекает ось x в точках 2 и 3.
–Б. График функции y = x2 – 5x + 6 имеет такой вид:
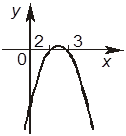
+В. График функции y = x2 – 5x + 6 имеет такой вид:
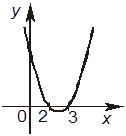
+Г. Решением заданного неравенства является объединение промежутков
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
