Алгебра 9 класс. Тема: Систематизация и обобщение знаний и умений учащихсяпо алгебре
Цель этого теста — проверить, умеет ли учащийся:
¾ выполнять тождественные преобразования заданных выражений и находить их область определения (область допустимых значений);
¾ характеризовать свойства заданных функций, строить их графики и использовать эти свойства и графики для исследования предложенных ситуаций;
¾ решать уравнения и неравенства разных типов и использовать их для решения текстовых задач;
¾ применять основные свойства и формулы, связанные с арифметической и геометрической прогрессиями, к анализу предложенных числовых последовательностей.
Вариант 1
Записывая ответы на
задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете
правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете
неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными
— утверждения Б и Г, запишите 
. Если хотя бы одна буква из
4-х будет не отмечена, задание считается невыполненным.
1-й уровень
1. Задано выражение a
×a
. Выберите правильное утверждение.
–А. a
= 
.
+Б. a ×a
= a
.
–В. a ×a = a
.
–Г. a ×a = a
.
2. Задана функция y = 2x – 6. Выберите правильное утверждение.
–А. Графиком заданной функции является парабола.
+Б. Графиком заданной функции является прямая.
–В. График заданной функции проходит через точку с координатами x = 0, y = 6.
–Г. График заданной функции пересекает ось y в точке, для которой y = 6.
3. Задано уравнение x
– 5x
+ 6
= 0.
Выберите правильное утверждение.
–А. Дискриминант заданного уравнения отрицательный.
–Б. Корнем заданного уравнения является число 0.
–В. Оба корня заданного уравнения отрицательные.
+Г. Сумма корней заданного уравнения равна 5.
2-й уровень
4. Задана система линейных уравнений
Отметьте, какие из следующих
четырех утверждений правильные, а какие — неправильные.
–А. Из первого уравнения получаем y = x.
–Б. Если во второе уравнение подставить y = –x, то получим –2x = 6.
+В. Решением заданной системы является пара чисел x = 3, y = –3.
–Г. Решением заданной системы является пара чисел x = –3, y = 3.
5. Задана
функция y = x – 2x.
Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Графиком заданной функции будет парабола, ветви которой направлены вниз.
+Б. Заданную функцию можно записать так: y = (x – 1)
– 1.
+В. Вершина параболы находится в точке с координатами x = 1, y = –1.
+Г. График заданной функции имеет такой вид:
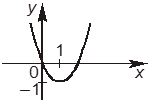
6. Задано
уравнение 
= 0. Отметьте,
какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Дробь 
равна нулю, если числитель x – 1 = 0,
а знаменатель x + 1 ¹
0.
–Б. x – 1 = 0
только при x = –1.
–В. При всех значениях x, для которых x – 1 = 0,
знаменатель заданной дроби не равен нулю.
+Г. Заданное уравнение имеет только один корень x = 1.
3-й уровень
7. Между числами 2 и 162 хотят вставить три таких числа, чтобы они вместе с данными числами составляли возрастающую геометрическую прогрессию. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Число 162 будет четвертым членом этой прогрессии.
+Б. Если знаменатель прогрессии обозначить через q, то по условию можно составить
уравнение 2q
= 162.
–В. Знаменатель искомой прогрессии может быть и положительным, и отрицательным.
+Г. Существует только одна тройка чисел, которую можно вставить между заданными числами так, чтобы они вместе с заданными числами составляли возрастающую геометрическую прогрессию.
8. Задана
функция y = 
. Отметьте,
какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Область определения заданной функции – все действительные числа.
+Б. Если числитель и
знаменатель дроби 
разложить
на множители и сократить полученную дробь, то заданную функцию можно
представить так: y = 
x при x ¹ 1.
|
–В. График заданной функции имеет такой вид:
|
+Г. График заданной функции имеет такой вид *:
|
9. Турист проплыл на байдарке 4 км по озеру и 5 км по течению реки за то же самое время, которое нужно ему, чтобы проплыть 6 км против течения. Известно, что скорость течения равна 2 км/ч. Скорость туриста при движении по озеру обозначили через х. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Скорость движения туриста по течению равна (х – 2) км/ч, а против течения равна (х + 2) км/ч.
+Б. По
условию можно составить уравнение: 
+ 
= 
.
+В.
Из условия следует, что x
удовлетворяет уравнению
3x – 22x – 16
= 0.
–Г. Существуют два разных значения x, которые удовлетворяют заданному
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
