Исследование свойств функций с использованием производной. Решение уравнений и неравенств разных типов: Вариативные тестовые вопросы по алгебре (Варианты 1-4 по 12 вопросов с отметками правильных ответов)

Алгебра 11 класс. Тема: Систематизация и обобщение знаний и умений учащихся по курсу алгебры и начал анализа

Цель этого теста — проверить, умеет ли ученик:

¾  выполнять тождественные преобразования заданных выражений и находить их область определения (область допустимых значений);

¾  исследовать свойства заданных функций как элементарными средствами, так и  с использованием производной, и использовать эти свойства для построения графиков функций и исследования предложенных ситуаций;

¾  решать уравнения и неравенства разных типов, используя все рассмотренные методы.

Следует обратить внимание на то, что в задачах этого теста используется понятие критической точки функции, которое необходимо для исследования функции. Критические точки — это внутренние точки области определения заданной функции, в которых производная равна нулю или не существует. Внутренние точки области определения функции, в которых производная равна нулю, еще называют стационарными точками.

Вариант 1

–А. Заданное выражение  существует при отрицательных значениях х.

–Б.  1 –  = 1 – .

–В.   =  + .

+Г. На области определения заданное выражение равно  1 – х.

–А. Правую часть заданного уравнения можно записать так: 2 × 2.

–Б. Заданное уравнение можно записать в виде: 2 = 2.

+В. Из заданного уравнения следует, что  x + 1 =  + 3x.

–Г. Заданное уравнение имеет корень, больший 1.

–А. Выражение в скобках равно   (– sin² a).

–Б. ctg a = .

–В. Заданное выражение равно  (– 2sin a × cos a).

+Г. Заданное выражение равно    sin 2a.

–А. Область определения данной функции задается такой системой:

+Б. Область определения данной функции задается такой системой: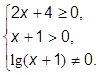

+В. Значение x = 1 входит в область определения заданной функции.

–Г. Значение x = 0 входит в область определения заданной функции.

+А. Если левую и правую части заданного уравнения возвести в квадрат, то получим уравнение  = (4 – x)².

–Б. Уравнение = (4 – x)²  можно записать в виде  x + 2 = 16 + 8x + x².

+В. Корнями уравнения x² – 9x + 14 = 0 являются x₁ = 2, x₂ = 7.

–Г. Все корни уравнения x² – 9x + 14 = 0 являются корнями заданного уравнения.

–А. Область определения данного неравенства задается неравенством  x + 5 < 0.

+Б. Число 2 можно представить так: 2 = log .

+В. Из условия следует, что x + 5 < .

+Г. Если учесть область определения заданного неравенства, то его решением является промежуток  –5 < x < – 4.

–А. f¢(x) = 0 только при x = 1 и при x = –1.

+Б. На области определения знаки производной и поведение заданной функции будут такими, как на рисунке:

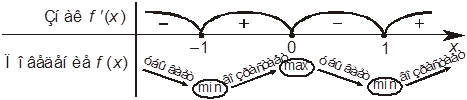
+В. График заданной функции имеет вид:

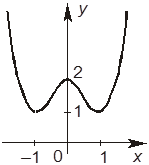
–Г. Уравнение f (x) = 2 имеет только два корня.

+А. Из определения логарифма следует, что для всех значений x, которые являются корнями заданного уравнения, выполняется равенство 2x² + 3x – 1 = (x + 1)².

–Б. Для всех значений x, которые являются корнями заданного уравнения, выполняется равенство  x² + 5x – 2 = 0.

–В. Все корни уравнения  x² + x – 2 = 0  являются корнями заданного уравнения.

+Г. Заданное уравнение имеет только один корень.

f (x) = .

Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

–А. Областью определения функции f (x) являются все значения   х ³ – 6.

–Б. Функция f (x)  равна нулю при двух значениях  х.

+В.  Нули f (x)  разбивают область определения функции f (x) на промежутки