Переход от предикатных уравнений к обычным. Примеры построения уравнений элементарных чертежей

8. Переход от предикатных уравнений к обычным

Выше была приведена формулировка обратной задачи аналитической геометрии: Для заданного чертежа найти уравнение f(x)=0, геометрическим образом которого является данный чертеж. В предыдущем параграфе уделялось внимание выбору класса чертежей, который мы будем рассматривать, и выбору класса уравнений, которыми будем описывать такие чертежи.

Будем считать, что при выбранном наборе базовых функций H имеются такие H-реализуемые функции s_i(х), которые позволяют с достаточной точностью описать все участки границ всякого чертежа. Эти участки границ образуют систему опорных замкнутых областей  в Rⁿ. Той же буквой S будем обозначать булевы предикаты, соответствующие функциям s_i(х):

Кроме того, будем считать, что множество H-реализуемых функций содержит по крайней мере одну достаточно полную систему R-функций.

Пусть  - некоторая булева функция. Очевидно, что выражение  является булевым предикатом в Rⁿ, а предикатное уравнение  определяет замкнутую область W. Пусть, далее,  - R-функция, для которой F – сопровождающая булева функция: , где . Тогда предикатное уравнение  определяет тот же чертеж, что и неравенство . 

Доказательство этого утверждения рекомендуется получить самостоятельно. Заметим, что при использовании трехзначной логики аналогичную теорему можно сформулировать и для геометрического образа уравнения, что позволяет формализовать построение уравнений границ областей.

Следовательно, переход от булева предиката к R-предикату путем формальной замены булевых операций на соответствующие R-функции гарантирует, что полученное неравенство определяет тот же чертеж, что и предикатное уравнение . Как правило, уравнение в этом случае описывает границу замкнутой области (возможные тонкости, связанные с использованием двузначной логики, будут показаны далее).

Рассмотрим более подробно построение уравнений произвольных полу-H-реализуемых чертежей. Они были определены ранее как объединения . Чертежи  называются элементами  чертежа .

Пусть  – двузначные булевы функции соответствующих областей, а . Тогда систему неравенств  можно заменить одним неравенством , ,  – символ какой-либо R-конъюнкции. (С точки зрения описания чертежа не обязательно, чтобы все R-конъюнкции принадлежали одной и той же системе, но одновременное использование различных систем R-функций может лишить нас возможности воспользоваться некоторыми из их дифференциальных свойств). Систему уравнений , также можно заменить одним уравнением , ,  (квадратный корень введен из соображений, касающихся нормализованности уравнений, о чем будет говориться далее).

Таким образом, элемент  определяется двумя выражениями  и , которые с помощью какой-либо из R-конъюнкций можно свернуть в одно: . При этом  вне .

Применяя операцию R-отрицания и правило де Моргана , получаем: , где  – какая-либо R-дизъюнкция.

Отметим также уравнение , которое обладает некоторыми выгодными свойствами дифференциального характера.

Иногда удобно для выделения областью  элемента  данного чертежа  использовать уравнения  и  , выражение  повышает гладкость функции  в точках, где  и  равны нулю одновременно.

Располагая уравнениями   элементов  полу-H-реализуемого чертежа  и учитывая, что  вне , уравнение всего чертежа  можно представить в виде . Можно использовать более простую формулу .

Таким образом, если базисная система H такова, что множество H-реализуемых функций содержит какую-нибудь из достаточно полных систем R-функций, то всякий полу-H-реализуемый чертеж является H-реализуемым.

Пусть T – группа преобразований-биекций вида  таких, что  – H-реализуемая функция. Тогда уравнение  является уравнением образа  чертежа  при преобразовании f и при этом – H-реализуемая функция. Таким образом, для всякого  из множества образов полу-H-реализуемых чертежей, соответствующих преобразованиям из T можно написать H-реализуемое уравнение . В соответствии с определением алгоритмически полной системы приходим к следующей теореме.

Теорема. Если система  такова, что множество H-реализуемых чертежей содержит какую-либо из достаточно полных систем R-функций, то она алгоритмически полная. Если, кроме того, T – множество биекций вида , где  – H-реализуемая функция, то система H является алгоритмически полной и относительно преобразований T.

Следствие. Базисная система   алгоритмически полная. Это обусловлено существованием элементарных достаточно полных систем R-функций.

Замечание 1. Элементы  могут иметь любую размерность от 0 до n. Так если , а , то уравнение области : .

Уравнение элемента гиперповерхности (размерности n-1) f=0, выделяемого областью , можно написать в виде .

Замечание 2. Если  – полуалгебраический чертеж, то, использовав R-операции =, = =, получим кусочно-полиномиальное класса  уравнение (сплайн-уравнение)  чертежа . При этом граница раздела областей полиномиальности функции будет формироваться автоматически в процессе построения .

9. Примеры построения уравнений элементарных чертежей

Пример 1. Построить уравнение прямоугольника ABCD с вершинами в точках A (a;b), B(-a;b), C(-a,-b), D(a, -b) (рисунок 5,а).

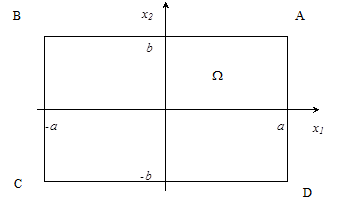
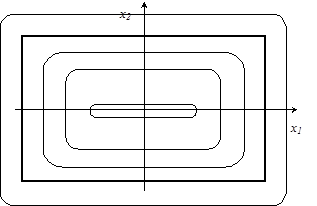
а                                                                                 б

Рисунок 5. Прямоугольник: а – чертеж, б – линии уровня R-предиката.

В качестве опорных областей выберем две полосы: вертикальную  и горизонтальную . Область W можно представить предикатом . Заменяя булеву конъюнкцию какой-либо R-конъюнкцией, например, , получим уравнение границы в виде:

==0.

На рисунке 5,б приведены линии уровня функции w₁.

Это уравнение – не единственное уравнение данного чертежа. Можно было бы взять в качестве опорных областей четыре полуплоскости: , ,  и . Тогда  - булев предикат области W.  Заменяя булеву конъюнкцию R-конъюнкцией, получим уравнение прямоугольника.

Заключение

Представленный в настоящем пособии материал охватывает разделы теории R-функций, дающие возможность получить представление о методах решения обратной задачи аналитической геометрии. Кроме этих приложений, методы теории R-функций используются также в приближенных способах решения краевых задач. Эти разделы будут изложены в следующих частях настоящего пособия.

Литература

1.  Рвачев В.Л. Теория R-функций и некоторые ее приложения. – Киев: Наук. думка, 1982. – 552 с.

2.  Рвачев В.Л. Геометрические приложения алгебры логики. – Киев: Техника, 1967. – 212 с.

3.  Рвачев В.Л., Рвачев В.А. Теория приближений и атомарные функции. – М.: Знание, 1978. – 64 с.