Испытание изоляции крупных электрических машин, страница 11

Принимая в этих формулах (2.7) напряжение за единичное U = 1 значение, получаем

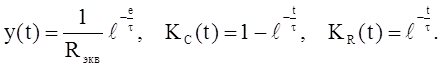                 (2.8)

Если на пассивную цепь в момент t = 0 подается воздействие по зависимости f₁(t), являющееся непрерывной функцией  времени, то реакция цепи f(t) определяется интегралом Дюамеля по выражению

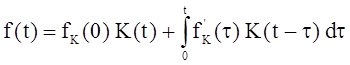,                          (2.9)

где f_k(0) – начальное значение воздействия;  - обозначение производной воздействия; K(t - t) – переходная функция, в которой аргумент t заменяется на t - t.

Если функция воздействия имеет различные выражения на разных интервалах времени, то реакция цепи записывается для отдельных интервалов времени. В нашем случае импульсы в форме полупериода синусоиды частотой 50 Гц подаются в цепь, содержащую последовательно соединенные сопротивления R и C. Уравнение напряжения в интервале времени от 0 до t_i = T₀ / Z имеет вид u₁(t) = U_m sin w_it (U_m = 24 кВ, T₀ = 0,02 с). Такая задача с помощью интеграла Дюамеля.

В интервале времени 0 £ t £ t_i имеем

u₁(t) = U_m sin wt

u`₁(t) = w₀ U_m cos w₀t                                     (2.10)

u₁(0) = 0

Переходная функция по напряжению выразится

 поэтому

=

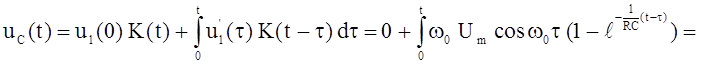
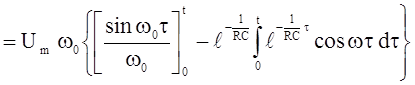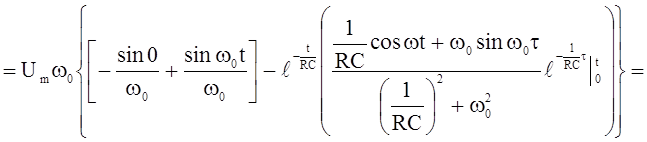
,                                (2.11)

где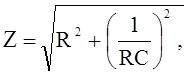   

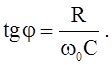
Напряжение в интервале времени t₁ £ t £ ¥ находим по интегралу Дюамеля, разбивая интервал интегрирования на два участка:

от 0 до t_i и от t_i до t, где u₁(t) = 0 и u`₁(t) = 0, тогда

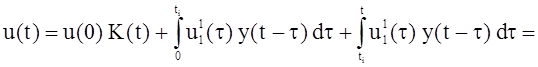
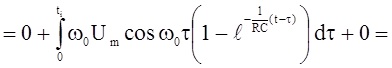
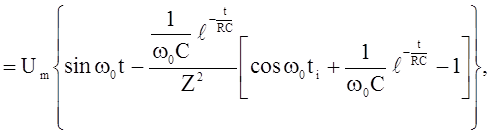                 (2.12)

имея в виду, что  и поэтому , получим выражение изменения ЭДС поляризации

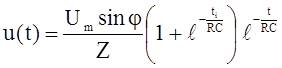.                                  (2.13)

По выражению (2.13) рассчитывается остаточное напряжение на емкости схемы замещения изоляции за время до появления следующего полупериода напряжения. Так будет продолжаться в течение всего времени релаксации с приходом каждого последующего полупериода. Остаточное напряжение на емкости изоляции эквивалентно появлению ЭДС поляризации в объеме материала. Именно время высоковольтной поляризации позволяет рассчитывать или утверждать, что ЭДС достигнет своего максимального значения [   ].

2.3. Выбор режима испытания изоляциинапряжением полупериода 50 Гц

Выбор режима испытания изоляции повышенным напряжением состоит в том, чтобы установить число полупериодов 50 Гц такое, когда будет отсутствовать электрическое старение изоляции за время воздействующего напряжения. Амплитуда испытательного напряжения сравнима с электрической прочностью изоляции при пробое ее.

На изоляцию слюдотерм и пленку ЛСПк-6 подавалось разное число полупериодов напряжения 50Гц. Число полупериодов n напряжения    50 Гц принималось равным 1, 25, 50, 100, 500, 1000, 3000, 10000 со скважностью следования в 1 с и, если изоляция не пробивалась за то число полупериодов, которое прикладывалось, то напряжение на следующем полупериоде поднималось до пробоя, например, по рис. 2.1 на четвертом полупериоде.

 

U

U_пр

U₁                           

n

n_пр       

Рис.2.1. Методика электрического старения изоляции

различным числом полупериодов напряжения 50 гЦ

Амплитуда напряжения старения U₁ для каждого числа полуперио дов выбиралось равного 50-% значению ожидаемого пробивного однопо

лупериодного напряжения 50 Гц. Затем находилась электрическая прочность изоляции слюдотерм при толщине образцов h = 0,8 мм, а пленки       h = 0,26

кВ   U_пр

Р = 0,95

                               Р = 0,5

30

Р = 0,05

20

10

lg n

1              2           3

Рис.2.2. Пробивные напряжения изоляции слюдотерм с различной вероятностью при старении ее от числа полупериодов напряжения 50 Гц

                 0,99   Р(Е)

1     2    3       4    5

0,5

0,1

0,01

Е_пр

15            30                45            кВ

Рис.2.3. Вероятностная электрическая прочность  изоляции слюдотерм

при воздействии полупериодов напряжения 50 Гц соответственно 3000 (1), 500(2), 50 (3), 1 (4) и 25 (5)

 

кВ   U_пр

Р = 0,95

                               Р = 0,5

60

Р = 0,05

40

20

lg n

1              2           3

Рис.2.2. Пробивные напряжения изоляции пленка ЛСПк-6 с различной вероятностью при старении ее от числа полупериодов напряжения 50 Гц