Испытание изоляции крупных электрических машин, страница 10

Под воздействием электрического поля в структуре любого диэлектрика происходит процесс поляризации – это ограниченное смещение зарядов или ориентация дипольных молекул. Следует различать мгновенную поляризацию без рассеивания энергии  и релаксационную поляризацию, которая нарастает и убывает, медленно и сопровождается рассеиванием энергии в диэлектрике. Электрическое поле смещает (перемещает) заряды и диполи, преодолевая силы связи внутренних структур диэлектрика.

Время, в течение которого упорядочение ориентированных полем зарядов и диполей после снятия внешнего поля уменьшится вследствие наличия теплового движения в 2,7 раза от первоначального значения, называется релаксационным. Релаксационные поляризации такие как дипольная, ионная и структурная миграционная характерны для многих термореактивных смол и слюды. При внесении неоднородного материала в электрическое поле свободные электроны и ионы проводящих и полупроводящих включений перемещаются в пределах каждого включения, образуя большие поляризованные области. На границе раздела между слоями в сложном диэлектрике и в при электродной зоне может накапливаться заряд, что создает эффект так называемой межслоевой или структурной миграционной поляризации (высоковольтная). Релаксация ее вычисляется долями секунды до нескольких десятков секунд (минута).

Ориентировочно можно оценить миграционную поляризацию в однородном поле изоляции, граничащей с поверхностью электрода, где возникает электрический диполь с моментом, равным

M = F (e - 1) e_o E d = (1 – 1/e) Q d ,                      (2.1)

так как F e e_o E = D F = Q.

Из (2.1) электрический момент поляризации, приходящийся на единицу объема, равен

P = M / V ,                                             (2.2)

где объем диэлектрика V = F d.

Физически величина Р является суммой электрических моментов, образуемых заряженными частицами и диполями в процессе поляризации изоляции. Если в изоляционном материале одновременно происходит К видов поляризации, а концентрация частиц, участвующих в i поляризации, равна n_i и эффективный элементарный момент диполя m_i, то

=.                                            (2.3)

Между элементарным моментом и напряжением электрического поля имеет место зависимость

m_i = a_i E,                                               (2.4)

где a_i – удельная поляризуемость материала; Е – напряженность результирующего поля, действующего на частицу.

Величина Е не равна напряженности внешнего электрического поля Е_вн, которое определяется только геометрическим размером изоляции. Для определения напряженности результирующего поля необходимо учитывать еще влияние поля Е₁ – окружающего частицу и собственное поле Е₂

исследуемой частицы, тогда

Е = Е_вн + Е₁ + Е₂.                                        (2.5)

В сложной структуре диэлектрика объемный заряд образуется на границе раздела со временем релаксации структурной или миграционной поляризации. Следовательно, результирующая электродвижущая сила ЭДС будет равна сумме ЭДС от внешнего поля Е_вн и ЭДС поляризации изоляции Е_п. Направление этих ЭДС противоположно друг другу и в сложной структуре изоляции электрическая прочность будет определятся результирующей ЭДС, а разрушение изоляции начнется, когда внешнее электрическое поле превысит суммарную внутреннею ЭДС связей молекул структуры диэлектрика по зависимости

Е_рез = Е_вн – Е_п .                                        (2.6)

Через время t_рел релаксации ЭДС поляризации E_п принимает некоторое постоянное значение близкое к максимальному для исследуемой изоляции и заданной формы напряжения. Используя универсальную схему замещения изоляции, можно провести расчет величину ЭДС по рис. 2.3.

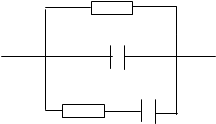                                                            R

C_¥

r         C_o

Рис. 2.3. Схема замещения изоляции

Эту схему можно упростить, сведя ее к эквивалентной схеме рис.2.4.

                                                  R_экв        С_экв

Рис. 2.4. Эквивалентная схема замещения рис. 2.3

При включении схемы рис. 2.4 напряжение и ток выразятся в виде следующих зависимостей

,                      (2.7)

где t = R_экв  С_экв – постоянная времени цепи по рис. 2.4.