Основные законы вращательного движения. Центробежные механизмы

Основные законы вращательного движения

Вращательным движением называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой — оси вращения.

Вращательное движение очень распространено в природе и технике. Вращаются воздушные массы атмосферы, образуя губительные смерчи, возникают круговороты на быстрых реках, в вечном вращательном движении пребывают громадные планеты в космическом пространстве и исчезающе малые электроны в атомах.

Бесконечно разнообразны примеры использования вращательного движения в технике. Почти в каждой машине есть вращающиеся детали: фрезы, сверла и резцы металлообрабатывающих станков, колеса, гребные винты и пропеллеры на транспортных машинах, маховые, водяные и ветряные колеса и роторы в энергетических установках.

Различные точки вращающегося тела за одно и то же время проходят пути разной длины: точки, близко расположенные к оси, проходят меньшие пути, чем точки, удаленные от оси. Поэтому и скорости и центростремительные ускорения этих точек различны и не могут служить для характеристики вращения всего тела в целом. Для этой цели используются угловые величины, одинаковые для всех точек вращающегося тела.

Рассмотрим сначала движение одной произвольной точки Л вращающегося тела (рис.1). За время t радиус r окружности, которую описывает точка А, повернется на угол j, называемый углом поворота точки. Быстроту вращения точки характеризует угловая скорость w. Угловой скоростью точки называется величина, равная отношению угла поворота ко времени, в течение которого произошел этот поворот:

w  =j/t

Связь линейной скорости V точки и угловой скорости выражается формулой

w =V/r

где r — радиус окружности, описываемой точкой. Если с течением времени w не меняется, вращение точки называется равномерным.

При неравномерном вращении точки быстрота изменения ее угловой скорости характеризуется угловым ускорением, обозначаемым буквой b.

Угловым ускорением называется величина, равная отношению изменения угловой скорости к промежутку времени, в течение которого это изменение происходит. Пусть за время t угловая скорость точки возросла от 0 до w. Тогда угловое ускорение равно:

b =w/t

Преобразуем эту формулу, так как w = V/r, то b = V/r×t , или w×r =V/t. Отношение V/r, представляющее собой изменение линейной скорости в единицу времени, называется тангенциальным ускорением и обозначается буквой аt. Следовательно, аt = r×b.

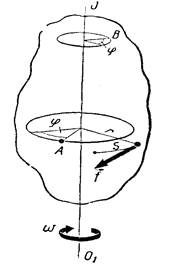Рис.1 Вращение тела в целом характеризуется угловыми характеристиками w, j, b.

Рассматривая движение другой произвольной точки В вращающегося тела (рис.1), можно показать, что за тот же промежуток времени t радиус окружности, которую она описывает, также повернется на угол j. Следовательно, угол поворота j одинаков для всех точек и может служить для характеристики вращения всего тела в целом. Он называется углом поворота тела. Очевидно, что w и b также одинаковы для всех точек тела и поэтому тоже характеризуют его вращение. Их называют соответственно угловой скоростью и угловым ускорением вращающегося тела.

Выясним теперь, от чего зависит быстрота раскручивания и остановки тела, или, другими словами, его угловое ускорение b. Для этого мысленно разобьем тело, вращающееся вокруг оси (рис.2), на столь малые частицы, что их размером можно будет пренебречь по сравнению с расстоянием до оси 001. (Не будем рассматривать лишь частицы, заполняющие весьма узкий канал вдоль оси 001 масса которых пренебрежимо мала по сравнению с массой всего тела, и потому они не повлияют на результаты расчетов.)

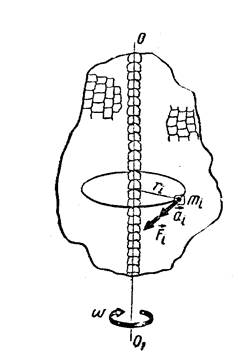     Рис.2 К выводу основного закона вращательного движения.

Рассмотрим частицу с номером i, имеющую массу тi и движущуюся с тангенциальным ускорением аti. Обозначим равнодействующую всех внешних сил, приложенных к данной частице, через Fi и будем считать, что она направлена по касательной к окружности, которую описывает частица (для простоты рассуждений мы не рассматриваем внутренних сил, действующих на данную частицу со стороны других частиц. Можно доказать, что это не влияет на конечные выводы, они останутся такими же и в более сложном случае, когда направление силы Fi не совпадает с направлением касательной).

.Согласно второму закону механики Fi= аti×тi. Умножая обе части этого равенства на ri и заменяя линейное ускорение угловым аti= ri×b, получаем:

Fi×ri =тi×ri²×b.

Произведение Fi×ri является моментом силы Fi относительно оси 001. Составим такие равенства для всех N частиц тела и просуммируем их от 1 до N, учитывая, что все частицы имеют одинаковые угловые ускорения:

F1×r1 + F2×r2 + F3×r3 +…+ FN×rN =( т1×r1²+ т2×r2²+ т3×r3²+…+ тN×rN²)×b.

Левая часть этого соотношения представляет собой полный момент внешних сил, действующих на тело, и обозначается через М. Выражение в скобках называют моментом инерции тела относительно оси 001 и обозначают буквой I. Подставляя М и I в последнюю формулу, получаем: М =I×b. Эта формула выражает основной закон вращательного движения твердого тела, играющий большую роль в технике.

Из него следует,что

b =M/I