Перечень теоретических и практических тем заданий по дисциплине «Математика» (Действия над матрицами. Второй замечательный предел)

Краевой союз потребительских обществ «Крайпотребсоюз»

Негосударственное образовательное учреждение

среднего профессионального образования

«Красноярский кооперативный техникум экономики, коммерции и права»

ДИФФЕРЕНЦИРОВАННЫЙ ЗАЧЕТ

на 2014 - 2015 учебный год

преподаватель

по учебной дисциплине Математика

специальности:  100701 « Коммерция» (по отраслям)

курс  второй,   группа  КА-2, КБ-2 форма зачета   письменно

Утверждаю

Зам. директора по учебной работе

_____________

«____»_________20__г.

Перечень теоретических тем заданий

по дисциплине «Математика

для  подготовки студентов II курса 

специальности 100701«Коммерция» (по отраслям)

к дифференцированному зачету в 2014 - 2015 учебном  году

1. Раздел:  Основы линейной алгебры

1.1. Действия над матрицами

1.2. Определители второго порядка, способы их вычисления 1.3. Определители третьего порядка, способы их вычисления

1.4. Системы линейных уравнений

1.5. Правило Крамера

2. Раздел:  Дифференциальное исчисление

2.1. Правила дифференцирования

2.2. Производная сложной функции

2.3. Монотонность и экстремум функции

2.4. Направление выпуклости и точки перегиба

2.5. Наибольшее и наименьшее значения функции

2.6. Дифференциал функции

3. Раздел:  Интегральное исчисление

3.1. Неопределенный интеграл и его свойства

3.2. Определенный интеграл. Формула Ньютона - Лейбница

3.3. Геометрические приложения определенного интеграла

3.4 Дифференциальные уравнения с разделяющимися переменными 3.5 Линейные однородные дифференциальные уравнения первого порядка 3.6 Линейные однородные дифференциальные уравнения второго порядка с   постоянными коэффициентами

4. Раздел:  Основы теории комплексных чисел

4.1. Алгебраическая форма комплексного числа и действия над ними

4.2. Геометрическая интерпретация комплексного числа, его модуль и аргумент

4.3. Тригонометрическая форма комплексного числа

4.4. Действия над комплексными числами в тригонометрической форме

5. Раздел:  Теория пределов

5.1. Предел функции в точке

5.2. Раскрытие неопределенности вида "бесконечность на бесконечность"

5.3. Раскрытие неопределенности вида "ноль на ноль"

5.4. Первый замечательный предел

5.5. Второй замечательный предел

Время выполнения – 90 минут

Составлен преподавателем:                         Кисловской Е.А.

Вариант 1.                         

 Задание №1  Тема: Определители третьего порядка Значение определителя третьего порядка 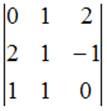 равно …

Решение:

 Задание № 2  Тема: Правило Крамера Систему 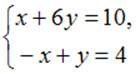 решают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)  2)  3) x 4) y

1	–14
2	14
3	–2
4	2

 Задание № 3

  Тема: Правила дифференцирования Производная функции  равна …

 Задание № 4  Тема: Определенный интеграл. Формула Ньютона - Лейбница  …

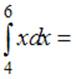 Задание № 5  Тема: Предел функции в точке  …

 Задание № 6 

 Тема: Второй замечательный предел

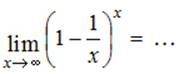
 Задание № 7  Тема: Умножение матриц Даны матрицы 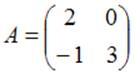 и 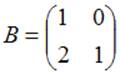. Тогда матрица равна …

 Задание № 8  Тема: Найти точку перегиба функции

y =

1	( 1;-3)
2
3
4	(-3; )
5

 Задание № 9  Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"

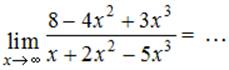
	– 2

 Задание № 10  Тема: Раскрытие неопределенности вида "ноль на ноль"

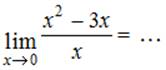
	– 3
	3
	0

 Задание № 11  Тема: Первый замечательный предел

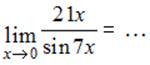
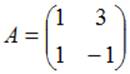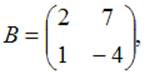 Задание № 12  Тема: Действия над матрицами Даны матрицы  и  тогда  …

 Задание № 13  Тема: Определители второго порядка Если определитель второго порядка 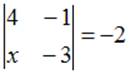, то  …

 Задание № 14  Тема: Системы линейных уравнений Система линейных уравнений 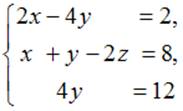 имеет решение …

 Задание № 15  Тема: Производная сложной функции Производная функции  равна …

 Задание № 16  Тема: Монотонность и экстремум функции Для функции  точка максимума принимает значение, равное …

 Задание № 17  Тема: Наибольшее и наименьшее значения функции Наибольшее значение функции  на отрезке  равно …

 Задание № 18  Тема: Дифференциал функции Для приближенного вычисления значения функции y(x) в точке  можно использовать формулу  где приращение функции в точке  Функция y(x) определяется из условия задачи. Значения  и  выбираются так, чтобы можно было вычислить  и при этом , взятое по модулю, было бы как можно меньше. Тогда приближенное значение выражения  равно …

 Задание № 19  Тема: Неопределенный интеграл Неопределенный интеграл  равен …

 Задание № 20  Тема: Геометрические приложения определенного интеграла Площадь фигуры, ограниченной графиком функции , прямыми ,  и осью абсцисс, равна …

 Задание № 21  Тема: Найти общее решение дифференциального уравнения

        у'=х+sinх

 Задание № 22  Тема: Действия над комплексными числами, заданными в алгебраической форме Произведение комплексных чисел  и  равно …

 Задание № 23  Тема: Тригонометрическая форма комплексного числа Тригонометрическая форма комплексного числа  имеет вид …

 

 Задание № 24  Тема: Действия над комплексными числами в тригонометрической форме

Произведение комплексных чисел  и  равно …

 Задание №25  Тема: Геометрическая интерпретация комплексного числа, его модуль и аргумент Дано комплексное число z=5+4i. Изобразить его на координатной плоскости, найти его модуль и аргумент.      

Рассмотрено на заседании ЦК общеобразовательных дисциплин и военно-спортивной подготовки                 протокол  № ____ от ___________ Председатель ЦК ____________  Т.И.Тюрюмина

Утверждаю Зам. директора по учебной работе _____________ «____»_________20__г.

                                                                                                                                                             Вариант 2.                         

 Задание №1  Тема: Определители третьего порядка

Значение определителя третьего порядка 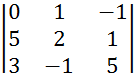 равно …

 Задание № 2  Тема: Правило Крамера

Систему  решают по правилу Крамера. Установите соответствие между названиями величин и их значениями. 1)  2)  3) x 4) y

1	–42
2	84
3	–2
4	3

 Задание № 3

  Тема: Правила дифференцирования Производная функции y=(1+) sin x равна …

	cos x (1+) - sin x (1+)
	(1+) sin x
	cos x (1+)+2x sin x
	(1+) sin x +2x

 Задание № 4  Тема: Определенный интеграл. Формула Ньютона - Лейбница …

 Задание № 5  Тема: Предел функции в точке …

 Задание № 6 

 Тема: Второй замечательный предел…

 Задание № 7  Тема: Умножение матриц Даны матрицы 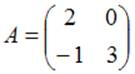 и 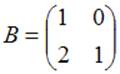. Тогда матрица равна …

 Задание № 8  Тема: Найти точку перегиба функции

y =

1	( 1;-32)
2
3
4	(-1;2)

 Задание № 9  Тема: Раскрытие неопределенности вида "бесконечность на бесконечность"

 Задание № 10  Тема: Раскрытие неопределенности вида "ноль на ноль"

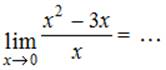
	– 3
	3
	0

 Задание № 11  Тема: Первый замечательный предел…

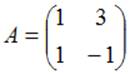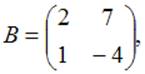 Задание № 12  Тема: Действия над матрицами Даны матрицы  и  тогда  …

 Задание № 13  Тема: Определители второго порядка Если определитель второго порядка , то  …

 Задание № 14  Тема: Системы линейных уравнений Система линейных уравнений 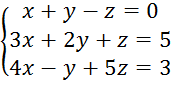 имеет решение …

	x = 2; y = -2; z = 3
	x = 3; y = -2; z = 2
	x = 2; y = -2; z = -3
	x = -3; y = -2; z = 3

 Задание № 15  Тема: Производная сложной функции Производная функции y= равна …

	-4cos x
	5sin x
	-5cos x
	5sin 5x

 Задание № 16  Тема: Монотонность и экстремум функции Для функции y=- точка максимума принимает значение, равное