В (19) учтено, что Qm = 1,5Qr, поскольку давление распределено по Герцу. Уравнение (19) содержит только одну неизвестную величину х — полуширину микропоры, которую можно найти из экспериментальных зависимостей коэффициента трения от парциального давления адсорбата. Поскольку в точке начала перехода от сухого к граничному трению
f(рmin) = fcм,
из выражения (19) имеем:
80,6erfc[0,061RT ln(ps/pmin)]Va = Qrx. (22)
На рис. 5 представлена полуширина зазора в контакте для молекул различных адсорбатов в жидком состоянии.
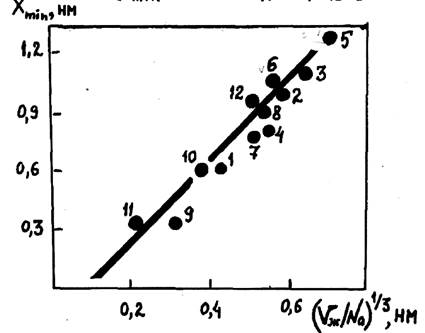
Рис.10. Зависимость полуширины зазора в контакте от размера молекул адсорбатов: 1 — этанол; 2 — бутанол; 3 — октанол; 4 — салициловая кислота; 5 — стеариновая кислота; 6 — нафталин; 7 — фенол; 8 — гидрохинон; 9 — сера; 10 — хлористый аммоний; 11 — фосфорный ангидрид; 12 — глицерин
Видно, что ширина зазора пропорциональна не длине, а размеру молекулы в жидком состоянии. Абсолютные значения ширины зазора оказались близкими к размерам молекул. Это свидетельствует о правильности сделанных предположений.
Эти данные описываются следующей корреляционной зависимостью
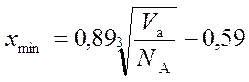. (21)
Эта зависимость может быть использована для вычисления полуширины зазора других адсорбатов при определении критических значений параметров.
Расчет адгезионной части работы при граничном трении.
Для расчета части работы силы трения, которая расходуется на разрыв адгезионных связей в режиме граничной смазки, рассматривается круговой процесс в закрытой термодинамической системе. Система состоит из деформирующего выступа, приповерхностного слоя деформируемого контртела, участка газовой среды, содержащей пары адсорбата, и отделена от окружающей среды воображаемой границей (пунктиром Рис.4.11 )
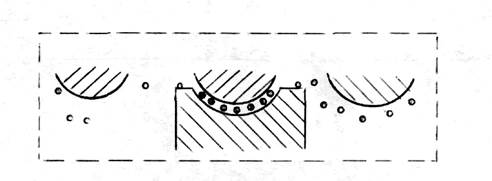
Рис.4.11 Схема граничного трения при адсорбции из газовой фазы.
Круговой процесс включает следующие стадии: образование контакта и формирование на нем смазочного слоя из адсорбированных молекул; перемещение контакта вдоль кристаллита; нарушение контакта и десорбция адсорбированных молекул (рис.6).
До образования контакта на поверхности присутствуют адсорбированные молекулы. Их число соответствует изотерме адсорбции на плоской поверхности (например, изотерме БЭТ). При адсорбции этих молекул выделяется теплота адсорбции nsqs, а при образовании контакта, в соответствии с уравнением Дубинина—Радушкевича, происходит дополнительная адсорбция молекул в зазоре. При этом выделяется количество теплоты, равное разности произведений числа дополнительно адсорбированных на контакте молекул nс на дифференциальную теплоту адсорбции на контакте qc и теплоты адсорбции ранее адсорбированных молекул (перед образованием контакта):
dq = ncqc – nsqs. (22)
Выделившаяся теплота рассеивается в окружающую среду и в системе устанавливается первоначальная температура.
Перемещение контакта вдоль кристаллита не требует затраты работы на разрыв образовавшихся адгезионных связей. При пересечении границы кристаллита система возвращается в первоначальное состояние, когда на поверхности имеется то количество адсорбированных молекул, которое соответствует изотерме адсорбции на плоской поверхности. Для этого необходимо затратить на десорбцию лишних молекул работу, равную ранее выделившемуся количеству теплоты. Таким образом, известно количество теплоты, выделившейся в закрытой системе при круговом процессе. Оно, в соответствии с первым началом термодинамики, равно работе, совершенной над системой:
dA = ncqc – nsqs. (23)
На пути трения, равном 1 м, работа силы трения, идущая на разрыв адгезионных связей, равна
Aa = (ncqc – nsqs)/L, (24)
где L, как и ранее, — средний размер кристаллита.
Увеличение относительного давления адсорбата приводит к росту адсорбции на контакте. Это вызывает увеличение коэффициента трения. При дальнейшем увеличении относительного давления рост адсорбции на плоской поверхности уменьшает разность теплоты адсорбции на контакте и на плоскости, что приводит к его снижению.
Расчет когезионной составляющей коэффициента трения был изложен на предыдущей лекции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.