При адсорбции полярных молекул на полярных адсорбентах к дисперсионному добавляется электростатическое взаимодействие. Это происходит при создании на неполярной поверхности слоя хемосорбированных полярных молекул, когда к дисперсионным силам добавляются ориентационное взаимодействие между диполями и мультиполями адсорбента и адсорбата. При этом адсорбция возрастает.
При физической адсорбции выделяется теплота равная энергии образовавшихся связей. Теплота физической адсорбции зависитот природы и строения молекуладсорбата, их ориентации у поверхности, а также от природы и структуры адсорбирующей поверхности.
Для феноменологического описания адсорбции обычно используют экспериментально найденные зависимости - изотермы адсорбции, которые выражают зависимости адсорбции от равновесного давлениягаза (или равновесной концентрации раствора) при постоянной температуре.
4.1.1 Граничное трение при адсорбции адсорбата из газовой фазы.
Теоретическими и экспериментальными исследованиями установлено, что адсорбированные молекулы не локализованы в отдельных точках, а находятся на ней в состоянии двумерного газа. При попадании на поверхность кристаллита молекулы притягивается ее атомами и, хаотически перемещаясь вдоль нее с тепловыми скоростями (около 60-90 м/сек), сталкиваются между собой. При столкновениях они изменяют направление и обмениваются энергией. Получив в ходе столкновений энергию, превышающую энергию связи, молекулы десорбируются. Вместо них на поверхность адсорбируются другие молекулы. При достижении равновесия количество адсорбирующихся в единицу времени молекул равно количеству десорбирующихся.
Время пребывания адсорбированной молекулы на поверхности τ описывается уравнением Я.И.Френкеля
![]() 4.1
4.1
Здесь τ0- период колебания ≈5.10-14с. При теплоте адсорбции Q=15 кДж/моль при Т=273К τ=7,4.10-12 с.
Имеется ряд моделей адсорбции, на основании которых выведены соответствующие изотермы. Наибольший интерес для трибологии представляют уравнение изотермы Брюнауэра, Эммета и Теллера (БЭТ) для адсорбции на однородной поверхности и уравнение изотермы Дубинина-Радушкевича для адсорбции в микропорах [3]..
Уравнение БЭТ для полимолекулярной адсорбции паров имеет вид
![]() (4.2)
(4.2)
где θ- степень заполнения поверхности, С – константа, p/ps- отношение парциального давления адсорбата к давлению его насыщенного пара при данной температуре.
По мере роста относительного давления р/рs адсорбированные молекулы после заполнения первого слоя заполняют второй, а потом следующие слои. (Рис.4) По мере удаления от поверхности взаимодействие адсорбат - адсорбент резко снижается Поэтому после заполнения первого слоя на изотерме адсорбции наблюдается перегиб (Рис.5) Точка перегиба при р/рs ≈0,1соответствует образованию мономолекулярного слоя.

Рис.4.3 Схема полимолекулярной адсорбции, принятая в теории Брунауера, Эмметта и Теллера
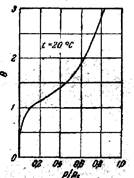
Рис.4.4 Изотерма полимолекулярной адсорбции пара бензола на поверхности графитированной сажи
Это уравнение применяется для измерения среднего размера частиц износа, которые имеют величину менее 1мкм. Получив на исследуемом порошке изотерму адсорбции азота из азото-гелиевой смеси при температуре жидкого азота, находят точку перегиба, соответствующей созданию монослоя. Поскольку известно, что площадь занимаемая молекулой азота, адсорбированного при -1970С, равна 0,162 нм2, можно найти поверхность 1 г порошка, а следовательно и размер частиц. Измерение частиц износа на электронном микроскопе дает большую ошибку вследствие их слипания и малого числа объектов в поле наблюдения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.