Квантовая теория и природа химической связи

Квантовая теория и природа химической связи

Сыктывкарский госуниверситет, физический факультет

Наиболее просто квантовая теория формулируется и осознается на основе идеи Р. Фейнмана о суммировании по всем возможным траекториям (состояниям) для получения реальной траектории (состоянии). Для некоторых семейств соседних траекторий фазы амплитуд переходов столь различны, что наложение амплитуд приводит к их взаимному гашению. Это запрещенные траектории или состояния. Однако для некоторых семейств соседних траекторий (состояний) фазы амплитуд переходов меняются медленно от траектории к траектории и их амплитуды складываются и дают отличную от нуля суммарную амплитуду, которая наблюдается в эксперименте. Это разрешенные траектории или разрешенные состояния или боровские орбиты. Во многом это близко принципу Гюйгенса-Френеля, но для частиц. В этом смысле теряет смысл разговор о корпукулярно-волновом дуализме.

Состоянию сопоставляется амплитуда, квадрат модуля которой - вероятность обнаружения системы в данном состоянии. Амплитуды всех возможных переходов суммируются и дают наблюдаемую амплитуду перехода. Амплитуды неразличимых одинаковых состояний складываются для Бозе-частиц и вычитаются для Ферми-частиц. Примером тому служит рассеяние одинаковых частиц друг на друге. Вероятность рассеяния одинаковых Бозе-частиц на угол p/2 вдвое больше чем вероятность такого рассеяния для подобных, но различимых частиц . Для одинаковых Ферми-частиц рассеяние на p/2 отсутствует  . Проявлением этого принципа симметризации амплитуд перехода является с одной стороны ограниченность видов сил в природе (передатчики взаимодействия - бозоны), с другой огромное многообразие мира вещества (частицы вещества - фермионы).

Ион молекулы водорода

Применим выше приведенные принципы к рассмотрению химической связи. Рассмотрим простейшую из «молекул» - молекулярный ион водорода.

На рисунке приведены два наиболее вероятных из всех возможных состояния такого образования. В первом приближении отбросим маловероятные состояния и ограничимся, приведенными на рисунке.

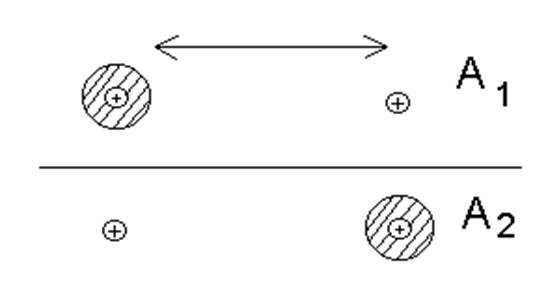
Одному сопоставляем амплитуду A₁ другому амплитуду A₂. Когда протоны находятся на больших расстояниях друг от друга, вероятность перехода электрона с протона «1» на протон «2» мала, но при их сближении вероятность такого перехода становится заметной. При отсутствии переходов между состояниями «1»и «2», эти состояния - состояния с определенной энергией E₀:

  , где  - скалярное произведение амплитуд, причем состояние вырожденное, так как нет переходов и они независимые. При наличии переходов (при сближении протонов) эти состояния перестают быть состояниями с определенной энергией (стационарными). Переходы можно учесть, рассматривая амплитуду как суперпозицию амплитуд A₁ и A₂ , и вводя в гамильтониан дополнительное слагаемое, отвечающее за переходы электрона

   .

Амплитуды состояния с определенной энергией, отвечающие этому гамильтониану, являются суперпозициями амплитуд A₁ и A₂

   _,

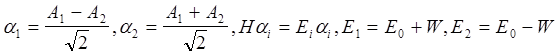(для определенности W>0). Первое состояние антисвязывающее, второе связывающее. То, что амплитуды вошли в виде разности и суммы вполне естественно. Чем одно состояние лучше другого. Амплитуды определяются с точностью до фазы, в данном случае с точностью до знака. При сближении протонов растет вероятность переходов электрона с протона на протон и следовательно растет W. Растет и энергия  E₀  системы из двух протонов и электрон на одном из них вследствие отталкивания протонов как разноименных зарядов. Это отражено на рисунке.

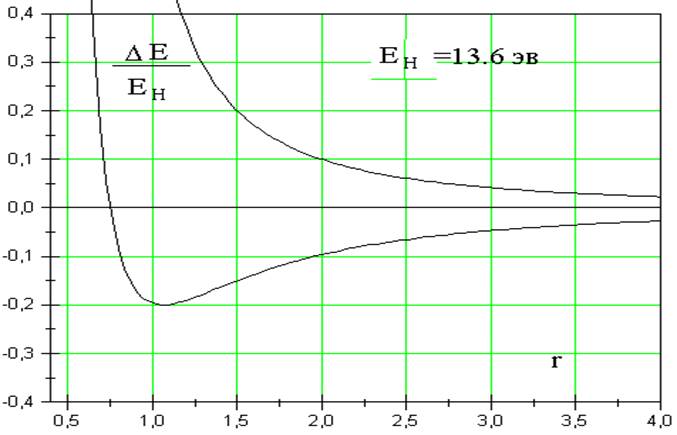
В связывающем состоянии вероятность нахождения электрона между протонами относительно велика. Электрон с одной стороны экранирует протоны, уменьшая их кулоновское отталкивание, с другой стороны притягивает оба протона к себе. Именно поэтому энергия такого состояния меньше энергии системы протон и атом водорода.