Электрические дипольные переходы. Фотоэффект

5.Электрические дипольные переходы. 

При электрическом дипольном переходе длина волны фотона значительно больше размеров квантовой системы,  в которой происходит переход электрона из одного состояния в другое. В (4.7) с хорошей точностью множитель .  Интегрирование по объему квантовой системы, интегрирование по всему объему (центра масс квантовой системы), дает как указывалось выше закон сохранения импульса. Возникает отдача, которая не существенна при рассмотрении оптических переходов. Импульс p  можно заменить на :

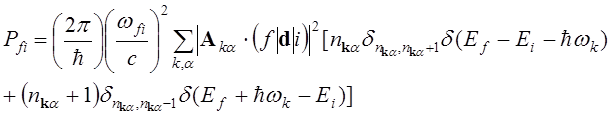            (5.1)

где  - частота перехода в квантовой системе d=er - оператор дипольного момента. Первое слагаемое в (5.1) отвечает поглощению фотона с энергией , а второе излучению фотона с энергией . Выше d- функции выражают закон сохранения энергии в процессе поглощения и излучения фотона. Причем число фотонов может меняться только на единицу. Рождение двух фотонов или поглощение двух фотонов описывается во втором порядке теории возмущений, как указывалось выше.

6.Фотоэффект.

Рассмотрим  фотоэффект при  поглощении фотона квантовой системой с электроном в связанном состоянии, состоянии дискретного спектра (рассматривается  фотоэффект в смысле однократной ионизации квантовой системы), и переходе электрона в состояние непрерывного спектра.  Вероятность перехода:

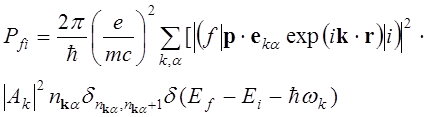
(6.1)

Рассмотрим простой пример перехода электрона из основного состояния водородоподобного атома в состояние непрерывного спектра. Волновая функция электрона водородоподобного состояния:

           (6.2)

где Z- заряд ядра, - энергия ионизации атома. Волновая функция электрона в конечном состоянии:

,                 (6.3)

нормирована на одну частицу в объеме V. Подставим  (6.2), (6.3) в (6.1) и получим:

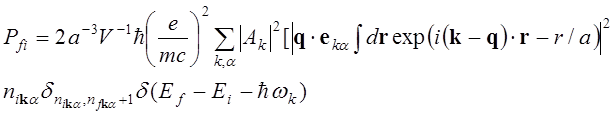   (6.4)

От суммирования по волновым векторам  в (6.1) перейдем к интегрированию и получим вероятность ионизации водородоподобного атома

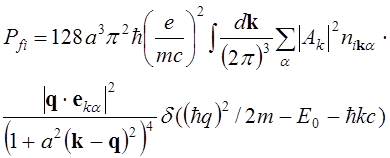                                       (6.3)

Как видно, закона сохранения импульса нет, так как в начальном состоянии импульс электрона в атоме не определенный. Задан момент импульса (в данном случае он равен нулю, s- состояние), который не коммутирует с импульсом.

Рассмотрим фотоэффект на свободном электроне (поглощение света свободным электроном). Начальное и конечное состояние электрона – (6.3). Вероятность перехода имеет следующий вид

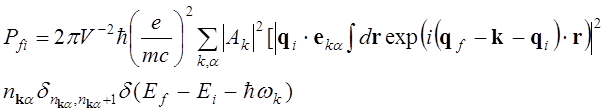
После замены суммирования интегрированием и вычисления интегралов вероятность перехода принимает следующий вид:

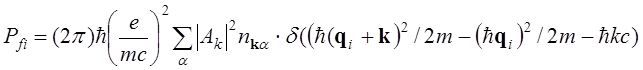
Выше дельта функция выражает закон сохранения импульса, так как конечное и начальное состояния электрона и фотона – состояния с определенным импульсом.