8. Рамановское (Мандельштамма-Брюллиэна) рассеяние света
Комбинационное рассеяние (Рамановское, Мандельштамма-Брюллиэна) описывается во втором порядке теории возмущений. Вероятность перехода квантовой системы с участием двух фотонов описывается:
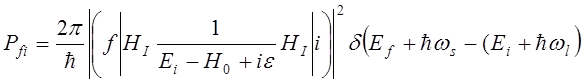 , (8.1)
, (8.1)
где
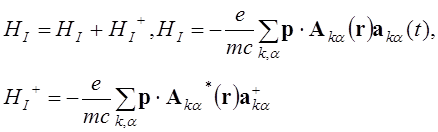 ,
(8.2)
,
(8.2)
первое слагаемое отвечает за уничтожение фотона, второе за рождение фотона. Здесь квантовая система – электронная система + падающие фотоны и рассеянные фотоны.
Начальное состояние квантовой системы - основное состояние (электронной квантовой системы + фотоны падающего излучения и рассеянные фотоны, конечное состояние - основное состояние электронной квантовой системы с изменившемся колебательным состоянием (колебания молекулы, колебательное состояние в кристаллической решетке ) + на один меньше падающих фотонов и на один больше рассеянных фотонов. Промежуточное состояние - возбужденное состояние электронной подсистемы и на один меньше падающих фотонов или - возбужденное состояние электронной подсистемы + падающий фотон + рассеянный фотон. При переходе электронной подсистемы в виртуальное (промежуточное) состояние изменения колебательного состояния не происходит, вследствие большого различия характерных времен жизни в возбужденном электронном состоянии и колебательном состоянии. Изменение колебательного состояния при нахождении в электронно-возбужденном состоянии происходит в условиях антистоксовой флуоресценции (промежуточное электронное состояние – метастабильное). Происходит: а) процесс поглощения фотона и переход в электронное возбужденное состояние, затем излучение рассеянного фотона и переход в основное состояние (электронное) с изменением колебательного состояния; b) процесс излучения рассеянного фотона с переходом в возбужденное (электронное) состояние, далее поглощение падающего фотона с переходом в основное с изменением колебательного состояния. При стоксовом рассеянии колебательное состояние в конечном состоянии выше по энергии чем в начальном состоянии, а при антистоксовом в начальном возбуждено более высокое колебательное состояние, чем в начальном состоянии.
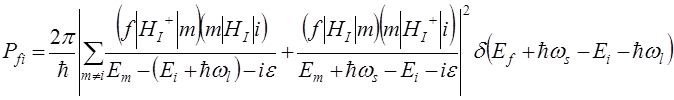 (8.3) где
(8.3) где
![]() даются формулой (8.2). После несложных преобразований вероятность
перехода принимает следующий вид:
даются формулой (8.2). После несложных преобразований вероятность
перехода принимает следующий вид:
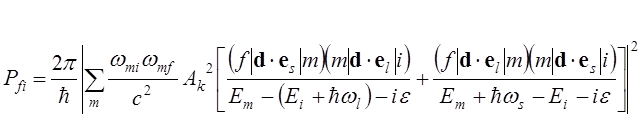 .
.
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.