Кратные интегралы: определение, свойства. Вычисление двойного интеграла в прямоугольных координатах

выполняется вдоль отрезка   или , переменные границы которого – уравнения линий, ограничивающих область D  СНИЗУ и СВЕРХУ  или СЛЕВА и СПРАВА;

(2)  повторное  интегрирование (внешний интеграл) функции одной переменной   выполняется по отрезку x€[a;b]  или y€[c;d], где a,bи c,d -  являются наименьшее и наибольшее значения “второй” переменной во всей области интегрирования D.

Замечание.  Если при выбранном порядке интегрирования     границы области вдоль соответствующей координатной прямой задаются различными уравнениями (“сложная область”), область интегрирования следует разбить на “простые части”.

-------------------------------------------------------------------------Задание «Двойной интеграл»: «1. Восстановить область интегрирования D двойного интеграла, записанного в виде двукратного интеграла; 2. изменить «порядок интегрирования» в прямоугольных координатах  и 3. записать двойной интеграл в полярных координатах».

1. Из свойства аддитивности интеграла  следует, что       

Область D₁ принадлежит полосе  и ограничена СНИЗУ линией y_H≡0 и СВЕРХУ – линией y_B(x)=1-x.

Область D₂ принадлежит полосе  и ограничена СНИЗУ линией y_H≡0 и СВЕРХУ – линией y_B(x)=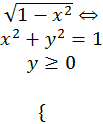- (верхняя полуокружность).

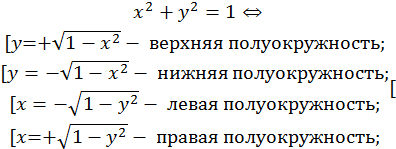
2.  При другом порядке интегрирования:

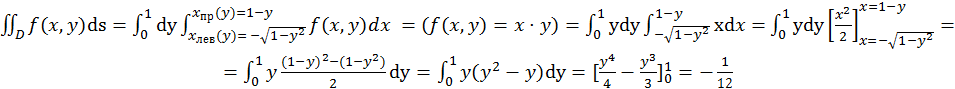
(в) Так как вдоль линии y=const граница области D «справа» задается двумя различными уравнениями  , запишем интеграл как сумму двух интегралов 

    §3  Вычисление двойного интеграла в полярных координатах; обобщенные полярные координаты.

Рассмотрим на плоскости две системы координат – прямоугольную и полярную.

Уравнение линий на плоскости: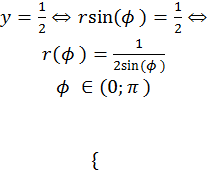 

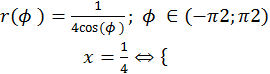
x²+y²=a² ó r=a; φ€[0;2π);    y=x² ó r(φ)=sin(φ)/cos²(φ)

x²+2x+y²=0 [(x+1)² +y²=1] ó r²+2rcos(φ)=0 ó r=0; r(φ)=-2cos(φ) 

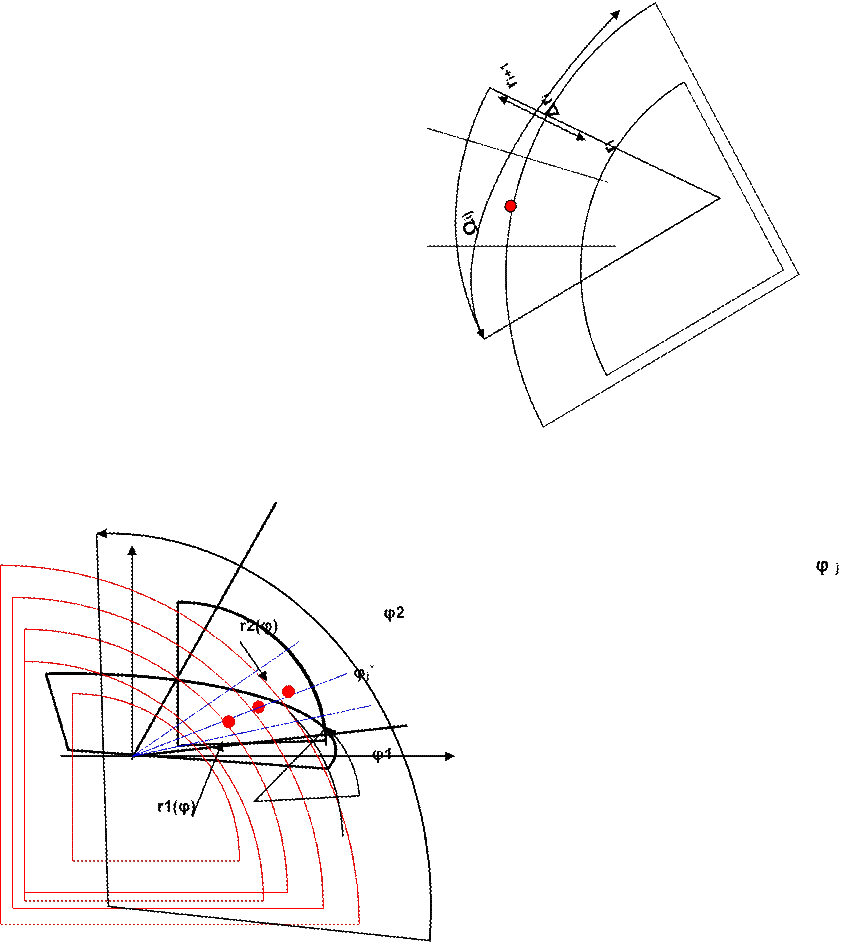Пусть область интегрирования D€R² ограничена линиями  r=r1(φ),r=r2(φ), φ=φ1 и φ(D)€[φ₁;φ₂] .

1) Введем разбиение P_n  области интегрированиялиниями “полярной сетки” r=const(концентрические окружности) и φ=const (лучи) на ячейки  Ω_ij –«криволинейные прямоугольники». При измельчении разбиений площадь ячейки равна ΔS_ij=r_iΔr_iΔφ_jèdS=rdrdφ.

2)Выберем в каждой ячейке сектора φ€[φ_j;φ_j+1] отмеченные точки A(r_i^*;φ_j^*) с одинаковыми полярными углами φ_j^*.

3) Упорядочим суммирование в интегральной сумме

 è

В результате предельного перехода при измельчении разбиений придем к заключению:

«Вычисление двойного интеграла в полярных координатах

сводится к двукратному интегрированию функций одной переменной, при этом - внешнее интегрирование выполняется по промежутку [φ_min; φ_max] или [r_min;r_max], границы которого соответствуют наименьшему и наибольшему значениям одной переменной во всей области;

-  внутреннее интегрирование выполняется вдоль линии полярной сетки r=const (окружность)или φ=const (луч), причем пределы этого интегрирования r₁(φ),r₂(φ) или φ₁(r), φ₂(r) – уравнения границ области вдоль линии.»

===================================================================

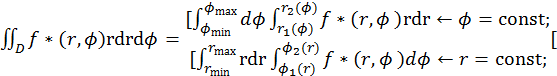
Пример 1. 

=

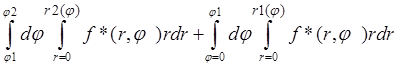
tg(φ1)=2ó φ1=arctg(2);tg(φ2)=4 ó φ2=arctg(4);;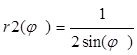

Пример 2.

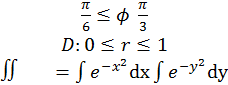è«бесперспективно, так как первообразная функции exp(-x²)не выражается через элементарные функции, в полярных же координатах

=

Пример 2. 

=

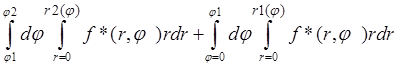
tg(φ1)=2ó φ1=arctg(2);tg(φ2)=4 ó φ2=arctg(4);;

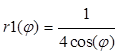
Замечание. Если область интегрирования ограничена эллипсом или его дугой, рекомендуется ввести «обобщенные полярные координаты», которые отображают эллипс в единичный круг:

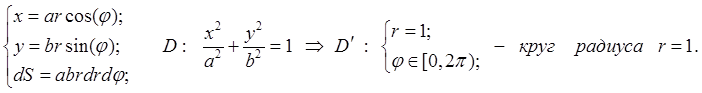
Например,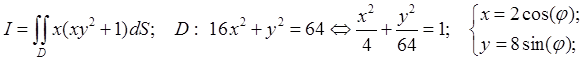

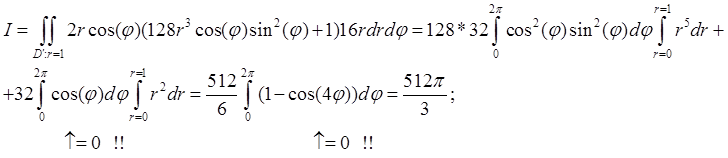
Типовая задача экзамена:(1)Восстановить область интегрирования;  (2)  изменить порядок интегрирования;  (3)  записать двойной интеграл в полярных координатах

§4 Вычисление тройных интегралов.

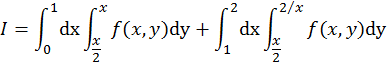
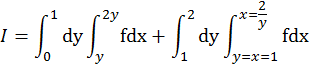
В R³ используются три системы координат: прямоугольная, цилиндрическая и сферическая.

По определению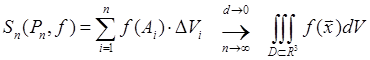; ΔV_i-объем ячейки при разбиении координатными поверхностями выбранной системы координат.

В прямоугольной системе ячейка разбиения - прямоугольный параллелепипед, его объем ΔV=Δx_i∙Δ_j∙Δ_kèdV=dxdydz.

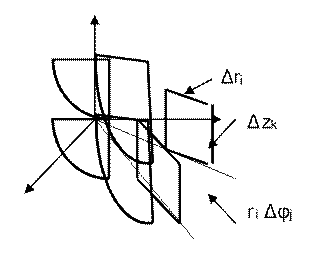В цилиндрической и сферической системах ячейка – криволинейный прямоугольный параллелепипед со сторонами

{ Δr_i;r_iΔφ_j;Δz_k} и { R_iΔθ_k;ΔR_i;R_isin(θ_k)Δφ_j}

ΔV=Δr_i∙r_iΔφ_j∙Δz_kèdV=rdrdφdz

ΔV=R_iΔθ_k∙ΔR_i∙R_isin(θ_k)Δφ_j==>dV=R²sin(θ)dRdθdφ

Следовательно, тройной интеграл в этих системах имеет вид: